7-kvadrato

En matematiko, 7-kvadrato estas plurkvadrato de ordo 7, kio estas plurlatero en la ebeno el 7 egale ampleksaj kvadratoj koneksaj je latero al latero. Se turnadoj kaj reflektoj estas ne konsiderataj kiel generantaj malsamajn formojn, estas 108 malsamaj liberaj 7-kvadratoj. Se reflektoj estas konsiderataj kiel malsamaj, estas 196 unuflankaj 7-kvadratoj. Se ankaŭ turnoj estas konsiderataj kiel malsamaj, estas 760 fiksitaj 7-kvadratoj.
Simetrio[redakti | redakti fonton]
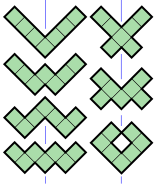
La bildo montras ĉiujn eblajn liberajn 7-kvadratojn, kolorigitajn laŭ iliaj simetriaj simetriaj grupoj:
- 84 7-kvadratoj (kolorigitaj grize) ne havas simetrion. Ilia geometria simetria grupo konsistas nur el la idento-bildigo.
- 9 7-kvadratoj (kolorigitaj ruĝe) havas akson de reflekta simetrio laŭ la kradolinioj. Ilia geometria simetria grupo havas du erojn, la identon kaj reflekton je linio paralela al la lateroj de la kvadratoj.
- 7 7-kvadratoj (kolorigitaj verde) havas akson de spegula simetrio je 45° al la kradolinioj. Ilia geometria simetria grupo havas du erojn, la identon kaj diagonalan reflekton.
- 4 7-kvadratoj (kolorigitaj blue) havas punktan simetrion, ankaŭ konatan kiel turna simetrio de ordo 2. Ilia geometria simetria grupo havas du erojn, la identon kaj la 180° turnadon.
- 3 7-kvadratoj (kolorigitaj purpure) havas du aksojn de reflekta simetrio, ambaŭ laŭ la kradolinioj. Ilia geometria simetria grupo havas kvar erojn, la identon, du reflektojn kaj la 180° turnadon. Ĝi estas la duedra grupo de ordo 2, ankaŭ nomata kiel la kvar-grupo de Klein.
- 1 7-kvadrato (kolorigita oranĝkolore) havas du aksojn de reflekta simetrio, ambaŭ laŭ la diagonaloj. Ankaŭ ĝia geometria simetria grupo estas la duedra grupo de ordo 2 kun kvar eroj.
Se reflektoj de 7-kvadrato estas konsiderataj kiel malsamaj, kiel ili estas ĉe unuflankaj 7-kvadratoj, do la unua kaj kvara kategorioj pli supre devus ĉiu duobliĝi en amplekso, rezultante en superfluaj 88 7-kvadratoj por tuteco de 196. Se ankaŭ turnadoj estas konsiderataj kiel malsamaj, do la 7-kvadratoj de la unua kategorio kalkulatas okoble, la aĵoj de la sekvaj tri kategorioj kalkulatas kvaroble, kaj la aĵoj de la lastaj du kategorioj kalkulatas duoble. Ĉi tio rezultas je 84 × 8 + (9+7+4) × 4 + (3+1) × 2 = 760 fiksitaj 7-kvadratoj.
Pakado kaj kahelado[redakti | redakti fonton]

Unu 7-kvadrato havas truon. Tiel bagatele la plena aro de 7-kvadratoj ne povas esti pakita en ortangulon, kaj ne ĉiu 7-kvadrato povas kaheli ebenon. Tamen, 104 liberaj 7-kvadratoj, kio estas ĉiuj krom 4, kahelas ebenon; la unu kun truo estas unu el la 4 lastaj.
Vidu ankaŭ[redakti | redakti fonton]
Eksteraj ligiloj[redakti | redakti fonton]
- Redelmeier, D. Hugh (1981). Counting polyominoes: yet another attack - Kalkulo de plurkvadratoj: ankoraŭ alia atako. Discrete Mathematics - Diskreta Matematiko 36 191–203. COI:10.1016/0012-365X(81)90237-5.
- Eric W. Weisstein, 7-kvadrato en MathWorld.