Ampera cirkvita leĝo
En elektromagnetismo, la Ampera cirkvita leĝo permesas kalkuli la valoron de la magneta kampo, dank'al la dateno de elektraj kurentoj. Tiu leĝo de Ampère estas simpligita integrala formo de unu el la ekvacioj de Maxwell nomita ekvacio de Maxwell-Ampère. Ĝi estis malkovrita de André Marie Ampère en 1826, kaj estas konsiderata kiel ekvivalenta al la gaŭsa leĝo en elektrostatiko. Por esti analitike kaj simple aplikita, tiu ampera leĝo koncernas prefereble problemjon kun alta fizika simetrio. [1]
Ampera cirkvita leĝo[redakti | redakti fonton]
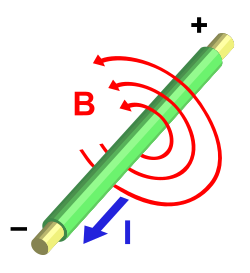
Per proksimumado de kvazaŭstabilaj aŭ stabilaj fenomenoj, la ampera cirkvita leĝo indikas ke la kontura integralo, laŭ fermita kurbo, de magneta kampintenso kreita de distribuo de elektraj kurentoj egalas al la algebra sumo de kurentoj, kiuj tra-iras la surfacon difinitan per la orientita cirkvito.
kie:
- estas la kontura integralo laŭ la fermita kurbo ,
- estas la magneta kampintenso,
- estas la elementa transloko laŭ la kurbo ,
- estas la algebra sumo de elektraj intensecoj de ĉiuj kurentoj ĉirkaŭigitaj de la konturo .
En vakuo, oni povas rekte kalkuli la magnetan fluksdenson, laŭ la ekvacio:
kie:
- estas la permeableco de vakuo.
Atentu, estas algebra sumo (adicio de signaj nombroj): oni devas orienti la konturon, kaj do difini normalan vektoron de la surfaco, sekvante konvenon de signoj de kurentoj konsiderataj pozitive aŭ negative laŭ iliaj direktoj.
Diversaj formoj de kurentoj[redakti | redakti fonton]
Oni povas konsideri diversajn kazojn de kurentoj ĉirkaŭigitaj de cirkvito.
- Kiam la cirkvito ĉirkaŭas plurajn dratformajn kurentojn, tiam la totala ĉirkaŭigita elektra intenseco estas kalkulota laŭ la formulo:
kie estas la kurento de la drato i.
- Kiam la cirkvito ĉirkaŭas linean kurenton kun lineara ŝarga denseco , tiam la ĉirkaŭigita elektra intenseco estas kalkulota laŭ la formulo:
- Kiam la cirkvito ĉirkaŭas surfacan kurenton kun surfaca ŝarga denseco , tiam la ĉirkaŭigita elektra intenseco estas kalkulota laŭ la formulo:
Demonstro de ampera leĝo pri forto (ampera forta leĝo)[redakti | redakti fonton]
Oni povas uzi la amperan cirkvitan leĝon por simple demonstri la amperan leĝon pri forto.
Konsideru cirklon C de radiuso r ĉirkaŭ longa maldika konduktilo, kiu estas perpendikla al la ebeno de la cirklo, kaj en kiu cirkulas kurenton I1. Apliku al ĝi la amperan cirkvitan leĝon:
en vakuo:
do:
Konsideru nun, paralele al la unua, duan konduktilon kun longo , en kiu cirkulas kurenton I2, je la distanco r. Ĉi tiu estas submetita al la magneta indukto B1, do al laplaca forto, pro la kurento en la alia konduktilo:
kaj pri unuobla longo la rilato fariĝas:
kio estas la ampera leĝo pri forto en ties simpla formo.
Rilato al ekvacioj de Maxwell[redakti | redakti fonton]
Apliko de teoremo de Stokes al la simpligita ekvacio de Maxwell-Ampère rezultigas esprimon de la leĝo de Ampère en lokala formo.
La ekvacio de Maxwell-Ampère estas:
Ĝi kreas rilaton inter la kampo (aŭ ankaŭ ) en punkto de spaco, kaj la kurenta denseco en tiu sama punkto; se la fenomeno ne dependas de la tempo:
aŭ ankoraŭ en vakuo
kaj laŭ la teoremo de Green:
.
Vidu ankaŭ[redakti | redakti fonton]
- Ampero
- Magneta konstanto
- Libera spaco
- Ampera forta leĝo (leĝo de Ampère pri elektromagneta forto)
- Leĝo de Biot-Savart
- Lorenca forto
- Vektora kalkulo
Referencoj[redakti | redakti fonton]
- ↑ Heinz E Knoepfel. (2000) Magnetic Fields: A comprehensive theoretical treatise for practical use. Wiley, p. 4. ISBN 0471322059.angle



























