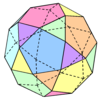
Dudek-dekduedro
| Dudek-dekduedro | |
| Plia nomo | Kvinlatera turnodurotondo |

| |
| Klaku por rigardi turnantan bildon | |
| Speco | kvazaŭregula |
| Vertica figuro | 3.5.3.5 |
| Bildo de vertico | 
|
| Bildo de reto | 
|
| Simbolo de Wythoff | 2 | 3 5 |
| Simbolo de Schläfli | |
| Figuro de Coxeter-Dynkin | |
| Indeksoj | U24 C28 W12 |
| Simbolo de Bowers | Id |
| Verticoj | 30 |
| Lateroj | 60 |
| Edroj | 32 |
| Edroj detale | 20{3}+12{5} |
| χ | 2 |
| Geometria simetria grupo | Mih |
| Duala | Romba tridekedro |
| Bildo de duala | 
|
Dudek-dekduedro estas pluredro kun dudek triangulaj edroj kaj dek du kvinlateraj edroj. Dudek-dekduedro havas 30 identajn verticojn, kun po du trianguloj kaj du kvinlateroj kuniĝantaj je ĉiu, kaj 60 identajn laterojn, el kiuj ĉiu apartigas triangulon de kvinlatero. Kiel tia ĝi estas arĥimeda solido kaj speciale kvazaŭregula pluredro.
Dudek-dekduedro havas dudekedran simetrion, kaj ĝia unua steligo estas la kombinaĵo de dekduedro kaj ĝia duala dudekedro, kun la verticoj de la dudekedro situantaj je la mezpunktoj de la randoj. Ĝia duala pluredro estas la romba tridekedro.
Surfaca areo kaj volumeno[redakti | redakti fonton]
La surfaca areo A kaj la volumeno V de la dudek-dekduedro de randa longo a estas:
Karteziaj koordinatoj[redakti | redakti fonton]
La karteziaj koordinatoj de verticoj de dudek-dekduedro estas la ciklaj permutoj de
- (0,0,±τ)
- (±1/2, ±τ/2, ±(1+τ)/2)
kie τ estas la ora proporcio (1+√5)/2 .
Geometriaj rilatoj[redakti | redakti fonton]
La dudek-dekduedro estas rektigita dekduedro kaj ankaŭ rektigita dudekedro, ekzistanta kiel la plena latera tranĉo inter ĉi-tiuj regulaj solidoj.
La romba tridekedro estas unu el la naŭ latero-transitivaj konveksaj pluredroj, ili estas 5 platonaj solidoj, kubokedro, dudek-dekduedro, romba dekduedro kaj romba tridekedro.
La dudek-dekduedro enhavas 12 kvinlaterojn de la dekduedro kaj 20 triangulojn de la dudekedro. La dudek-dekduedro ekzistas en la aro de senpintigitaj formoj inter dekduedro kaj dudekedro:

|

|

|

|

|
| Dekduedro | Senpintigita dekduedro | Dudek-dekduedro | Senpintigita dudekedro | Dudekedro |
Dudek-dekduedro povas esti fendita laŭ kelkaj ebenoj kaj formi kvinlaterajn rotondojn.
Dudek-dekduedro povas nomiĝi ankaŭ kvinlatera turno-durotondo. Se unu el la rotondoj turni je 36 gradoj, rezultas kvinlatera ortodurotondo.
 La sekco |
|
Estas 9 stelaj unuformaj pluredroj, kiuj havas la saman situon de verticoj kiel la dudek-dekduedro:
Vidu ankaŭ[redakti | redakti fonton]
- Kubokedro
- Dekduedro
- Granda senpintigita dudek-dekduedro
- Dudekedro
- Rombo-dudek-dekduedro
- Senpintigita dudek-dekduedro
- Kvinlatera ortodurotondo
- Unua steligo de dudek-dekduedro
- 15-a steligo de dudek-dekduedro
Referencoj[redakti | redakti fonton]
- Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)
Eksteraj ligiloj[redakti | redakti fonton]
- Eric W. Weisstein, Dudek-dekduedro en MathWorld.
- La unuformaj pluredroj
- Virtualaj realaj pluredroj - la enciklopedio de pluredroj