Granda O
En matematiko, granda O estas la simbolo O uzata por priskribi asimptotan superan baron por la grandeco de funkcio per la alia, kutime pli simpla, funkcio.
Estas ankaŭ la aliaj simboloj o, Ω, ω, Θ, Õ por diversaj aliaj superaj, subaj kaj striktaj baroj (vidu sube).
Difino[redakti | redakti fonton]
|
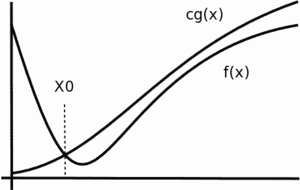
Estu f(x) kaj g(x) estas du funkcioj sur iu subaro de la reelaj nombroj. Tiam f(x) estas de la ordo de g(x) kiam x proksimiĝas al plus malfinio (kio estas ) se kaj nur se ekzistas pozitiva reela nombro c kaj reela nombro x0 tiaj ke |f(x)| < c g(x) por ĉiu x tia ke x>x0.
Per formuloj ĉi tio estas:
se kaj nur se
Tia notacio povas esti uzita ankaŭ por priskribi konduton de f(x) proksime al iu reela nombro a:
se kaj nur se
Se g(x) estas ne-nula por valoroj de x sufiĉe proksime al a, ambaŭ ĉi tiuj difinoj povas esti unuece skribitaj per la limigo supera:
se kaj nur se
Uzado[redakti | redakti fonton]
La notacio kun granda O estas utila en analizo de rula tempo de algoritmoj.
En matematiko, ambaŭ asimptotaj kondutoj proksime al ∞ kaj proksime al iu a estas uzatadaj. En komputa komplikteorio, nur asimptotoj proksime al ∞ estas uzataj kun nur pozitivaj funkcioj estas konsiderata, tiel la esprimo de absoluta valoro povas esti ellasita el la formuloj de la difino.
Ekzemploj[redakti | redakti fonton]
Malfinia asimptoto[redakti | redakti fonton]
Ekzemple, la tempo (aŭ la kvanto de ŝtupoj) bezonata por plenumi problemon de amplekso n estu T(n) = n2 - n + 2.
Se n kreskas kaj iĝas grandan, la termo n2, estos ĉiam domina, tiel ke ĉiuj alia termoj povas esti neglektitaj. Ekzemple por n=1000, la termo n2 estas je 1000 fojoj pli granda ol la termo n. Ignoro de la lasta devas ne havi konsiderindan efikon por plejparto de pritaksoj de rula tempo.
Plu, la koeficientoj iĝas negravajn se oni komparas la ordojn. Ekzemple estu termoj n2 kaj n3. Eĉ se S(n)=n2 kaj U(n)=0,01n3, la lasta estas pli granda ol la unua por n>100. Por plu pli grandaj n, ekzemple n=109, diferenco inter S(n) kaj U(n) estas multe pli granda ol inter U(n) kaj V(n)=n3: S(109)=1018, U(109)=1025, V(109)=1027.
Tiel la granda O kaptas tion kio restas:
Finia asimptoto[redakti | redakti fonton]
Granda O povas ankaŭ esti uzata por priskribi la eraran termon en proksimuma kalkulado de funkcio. Ekzemple,
esprimas la fakton ke la eraro, la diferenco , estas pli malgranda en absoluta valoro ol iu konstanto multiplikita per kiam x proksimiĝas al 0.
Problemoj pri la notacio[redakti | redakti fonton]
O(f(x)) signifas kolekton de funkcioj g(x) de variablo x, tiaj ke ilia kreskado estas limigita per kreskado de f(x) en iu respekto. La tradicia notacio por tio ke g(x) apartenas al ĉi tiu kolekto estas:
- g(x) = O(f(x))
Ĉi tiu uzo de la egala signo estas nerigora notacio, pro tio ke la pli supra frazo ne estas ekvacio. Estas malvere konkludi de g(x) = O(f(x)) kaj h(x) = O(f(x)) ke g(x)=h(x). Unu el variantoj estas opinii ke ĉi tie "= O" estas unu simbolo. Al eviti la problemon, iuj aŭtoroj preferas skribi anstataŭe kiel:
sen diferenco en signifo. Noto ankaŭ, ke ĉi tie en notacio kun simbolo "=" ne eblas interŝanĝi la flankojn, oni ne skribas kiel
- O(f(x)) = g(x)
La komunaj aritmetikaj operacioj estas ofte etenditaj al la klasa koncepto. Ekzemple, h(x) + O(f(x)) signifas kolekton de funkcioj havantaj la kreskadon de h(x) plus parto kies kreskado estas limigita al tiu de f(x). Tial,
estas la samo kiel
Alia anomalio de la notacio, kvankam malpli escepta, estas ke oni ne eksplicitas kiu variablo estas la funkcia argumento, kaj ĉi tion bezonatas konkludi de la ĉirkaŭteksto se kelkaj variabloj estas koncernataj. En la ekzemplo du dekstraj flankoj uzantaj la notacion de granda O havas ege malsamajn signifojn:
En la unua okazo f(m) havas polinoman kreskadon, en la dua por m>1, g(n) havas eksponentan kreskadon.
Fina anomalio estas ke la notacio ne montras klare kie la funkcia kreskado estas konsiderata; proksime al iu punkto aŭ al la malfinio. Ĉi tiu estas en kontrasto kun la kutima notacio por limigoj.
En pli kompleksa uzado, O( ) povas aperi en malsamaj lokoj en ekvacio, eĉ kelkfoje en ĉiu flanko. Ekzemple, jeno estas vera por
La signifo de la propozicioj estas: por ĉiuj funkcioj kiu kontentigas ĉiun O( ) maldekstre, estas iuj funkcioj kontentigantaj ĉiun O( ) dekstre, tiaj ke enmeto de ĉi ĉiuj funkcioj en la ekvacion faras la du flankojn egalajn. Ekzemple, la tria ekvacio pli supre signifas ke por ĉiu funkcio f(n)=O(1), estas iu funkcio g(n)=O(en) tia ke nf(n)=g(n). En terminoj de la ara notacio kiel pli supre, la signifo estas ke la klaso de funkcioj prezentitaj per la maldekstra flanko estas subaro de la klaso de funkcioj prezentitaj per la dekstra flanko.
Estas ankaŭ problemo ke la simbolo f(x) signifas la valoron de la funkcio f por la argumento x, sed ne la funkcion entute. La simbolo de la funkcio estas f sed ne f(x). Por ĉi tio, iuj aŭtoroj preferas skribi kiel
- .
Ecoj[redakti | redakti fonton]
Jen estas listo de klasoj de funkcioj kiuj estas kutime estadas en analizo de algoritmoj. Ĉi tie n pligrandiĝas al malfinio. La pli malrapide kreskantaj funkcioj estas listitigiaj komence. c estas ajna konstanto.
| Notacio | Nomo | Ekzemplo de algoritmo kun ĉi tiu tempo |
|---|---|---|
| O(1) | Konstanto (konstanta tempo) |
Difini ĉu nombro estas para aŭ nepara |
| O(α(n)) | Inverso de akermana funkcio | |
| O(log* n) | Ripetita logaritmo | |
| O(log (log (log n))) | ||
| O(log (log n)) | ||
| O(log n) | Logaritmo | Trovo de ero en ordigita listo per duoniga serĉa algoritmo |
| O((log n)c) por c>1 | Polinomo de logaritmo | Kontrolo ĉu n estas primo per la primeco-testo AKS. |
| O(nc) por 0<c<1 | Frakcia potenco | |
| O(n) | Lineara funkcio (lineara tempo) |
Adicio de du n-ciferaj nombroj. Trovo de ero en neordigita n-era listo. |
| O(n log n) | Ordigo de n-era listo per piramida ordigo. Komputo de rapida konverto de Fourier. | |
| O(n2) | Kvadrata funkcio (kvadrata tempo) |
Multipliko de du n-ciferaj nombroj (per kutima rekta maniero). Adicio de du n×n matricoj. Ordigo de n-era listo per simpla enenigo aŭ bobelo. Rekta komputo de diskreta konverto de Fourier. |
| O(n3) | Kuba funkcio (kuba tempo) |
Multipliko de du n×n matricoj (per kutima rekta maniero). |
| O(nc) por c>1 (pli granda ol O(n3) se kaj nur se c>3) |
Polinomo (polinoma tempo) |
Kontrolo ĉu n-cifera nombro estas primo per la primeco-testo AKS. Trovo de la plej mallonga vojo sur pezita orientita grafeo per la algoritmo de Floyd-Warshall |
| O(cn) por c>1 | Eksponenta funkcio, iam nomata kiel geometria (eksponenta tempo) |
Trovo de (akurata) solvaĵo por la problemo pri vojaĝa komizo (kun supozo ke P ≠ NP) |
| O(n!) | Faktorialo, iam nomata kiel kombina funkcio | [1] |
| O(nn) | ||
| Duopa eksponenta funkcio | [2] |
Se funkcio f(n) povas esti skribita kiel finia sumo de aliaj funkcioj, tiam la plej rapide kreskanta ero difinas la ordon de f(n). Ekzemple
Aparte, se funkcio povas esti barita per polinomo en n, tiam kiel n strebas al malfinio, oni povas malobservi termoj de ne la plej granda ordo de la polinomo.
Por c>1, O(nc) kaj O(cn) estas tre malsamaj. La lasta kreskas multe, multe pli rapida, sendepende de la konstanto c estas (se ĝi estas pli granda ol unu). Funkcio kiu kreskas pli rapida ol ĉiu potenco de n estas superpolinoma. Funkcio kiu kreskas pli malrapide ol ĉiu eksponenta funkcio de formo estas subeksponenta. Funkcio povas esti ambaŭ superpolinoma kaj subeksponenta. Ekzemple ĉi tia estas tempo de ĝenerala nombra kampa kribrilo, la plej rapida sciata algoritmo por entjera faktorigo, kiu por b-bita nombro estas:
O(log(nc)) estas akurate la samo kiel O(log n). La logaritmoj diferenciĝas nur per konstanta faktoro pro tio ke log(nc)=c log n kaj tial la granda O ignoras la diferencon. Simile logaritmoj kun malsamaj konstantaj bazoj estas ekvivalentaj. Eksponentoj kun malsamaj bazoj, male, estas ne de la sama ordo. Ekzemple, 2n kaj 3n estas ne de la sama ordo.
Por ĉiu k>0 kaj ĉiu c>1, O(nc log(nk)) estas subaro de O(log(n(c+a))) por ĉiu a>0. Tiel ofte estanta kresko O(nc log(nk)) povas esti konsiderata kiel polinoma kun malmulte pli granda potenco.
Multipliko de la variablo per konstanto povas afekti aŭ ne afekti la ordon de la kresko. Ekzemple, se la ordo estas n2, anstataŭigo de n per cn signifas ordon de c2n2, kaj la granda O ignoras la konstanton c2. Ĉi tio povas esti skribita kiel . Tamen se la ordo estas 2n, anstataŭigo de n per cn donas ordon , kiu ne estas ekvivalento al 2n (se c≠1).
Ŝanĝo de la variablo povas ŝanĝi la formulon por ordo de kresko, ne ŝanĝante la realan tempon de ruligo. Ekzemple, por primeco-testo AKS, la tempo estas O((log n)c) se n estas la kontrolata nombro kaj O(nc) se n estas kvanto de ciferoj en la nombro.
Eblas pli granda kreskado ol komune estantaj, ekzemple la solo-valora versio de la akermana funkcio, A(n,n). Male, estadas ege malrapide kreskantaj funkcioj, ekzemple la inverso de ĉi tiu funkcio A(n,n), ofte skribata kiel α(n). Kvankam α(n) estas nebarita (proksimiĝas al malfinio kiam n proksimiĝas al malfinio), ĉi tiaj funkcioj estas ofte proksimumataj kiel konstantaj faktoroj por ĉiuj praktikaj celoj.
Produto[redakti | redakti fonton]
Sumo[redakti | redakti fonton]
-
- Ĉi tiu implicas , kio signifas ke estas konveksa konuso.
Multipliko per konstanto[redakti | redakti fonton]
Por .
Rilatantaj asimptotaj rilatoj[redakti | redakti fonton]
Malgranda o[redakti | redakti fonton]
La rilato signifas ke f(x) kreskas multe pli malrapide ol g(x), do la limigo de f(x)/g(x) estas nulo, kiam x proksimiĝas malfinio aŭ al certa valoro.
Ekzemple por :
Jenaj propraĵoj ekzistas:
- kaj tial la propraĵoj de O aplikas kun kombinaĵoj de o kaj O.
Simile al granda O, la frazo "f(x) estas o(g(x))" estas kutime skribata kiel f(x) = o(g(x)), kio estas nerigora notacio.
Aliaj[redakti | redakti fonton]
| Notacio | Priskribo | Difino |
|---|---|---|
| f estas asimptote desupre barita per g kun ignoro de konstanta faktoro | ||
| f estas asimptote desube barita per g kun ignoro de konstanta faktoro | ||
| f estas barita strikte (desube kaj desupre) per g asimptote | ||
| f estas dominita per g asimptote | ||
| f dominas na g asimptote | ||
| f kaj g asimptote egalas | ||
| (Õ estas la mola-O) |
Same kiel granda O, sed ignoranta logaritmajn faktorojn. | por iu k. |
estas ĉiam por ĉiu konstanto k kaj ĉiu konstanto a>0.
La L-notacio, difinita kiel
- ,
estas oportuna por funkcioj kiuj estas inter polinomo kaj eksponenta funkcio.
Multaj variabloj[redakti | redakti fonton]
Granda O kaj malgranda o, kaj la aliaj povas ankaŭ esti uzataj kun multaj variabloj. Ekzemple, la frazo
asertas ke ekzistas konstantoj C kaj N tiaj ke
Por konkreteco la ŝanĝanta variablo devus ĉiam esti precizigita: la frazo
estas sufiĉe malsama de
Vidu ankaŭ[redakti | redakti fonton]
Referencoj[redakti | redakti fonton]
- ↑ Arkivita kopio. Arkivita el la originalo je 2008-03-10. Alirita 2008-05-07.
- ↑ Komplikeco de duopa eksponenta funkcio en komputado
Eksteraj ligiloj[redakti | redakti fonton]
- Enkonduko al asimptotaj notacioj Arkivigite je 2011-06-04 per la retarkivo Wayback Machine
- Vikilibroj pri granda O
- Donald Knuth. Granda Omicron kaj granda Omego kaj granda Θ, ACM SIGACT Novaĵoj, Volumeno 8, Eldono 2, 1976.
- Formaligo de O-notacio
- Granda O-notacio
- Notacio kun malgranda o
- "Ω"
- "ω"
- "Θ"

































































![{\displaystyle L_{n}[\alpha ,c]=O\left(e^{((c+o(1))(\ln n)^{\alpha }(\ln \ln n)^{1-\alpha })}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3060d43e7bb390c14c19fc86e445f6c350bebe4)



