Gravito
La gravito estas fundamenta forto, kiu efikas inter masoj. Ĝi kaŭzas, ke ĉiuj mashavaj objektoj altiras, t. e. tendencas alproksimigi, sin reciproke.
La rezultanta forto dependas je la distanco(j) kaj je la masoj.
Gravito ankaŭ tenas Teron sur ĝia vojo ĉirkaŭ Sunon.
Historio de la fiziko de gravito[redakti | redakti fonton]
Antikvaj filozofoj kaj esploristoj[redakti | redakti fonton]
Aristotelo konstatis, ke ĉiuj pezaj objektoj emas fali teren, kaj tial supozis, ke la Tero posedas specialan forton, kiu altiras ĉiujn objektojn. Li deklaris, ke pezaj objektoj falas pli rapide ol malpezaj.
En la 9-a jarcento la persa astronomo Al-Ĥorezmi formulis teorion, kiu klarigis la moviĝon de la planedoj per altira forto efikanta inter ili. Alia persa astronomo, Al-Ĥazini, en la 12-a jarcento supozis, ke la surtera pezoforto dependas de la distanco disde la tercentro.
Komencoj de naturscienco[redakti | redakti fonton]
En la 16-a jarcento Galilejo eksperimente konfirmis, ke la gravita falo estas moviĝo kun konstanta akcelo, kaj ke tiu akcelo ne dependas de la pezo de la falanta objekto (nur la bremsa efiko de aera froto). Sed ĉar per tio li kontraŭdiris al Aristotelo, liaj kolegoj ne emis kredi lin.
Ĉirkaŭ 1670 la anglo Robert Hooke komparis la efikon de gravito al funeloj, en kiuj objektoj emas iri al la centro; per tio li jam proksimiĝis al postaj ideoj de Ejnŝtejno (vidu malsupre). Li supozis, ke gravito estas eco ne nur de Tero, sed de ĉiuj masaj objektoj. En letero al Neŭtono li esprimis la teorion, ke la gravita forto inter du masoj estas inverse proporcia al la kvadrato de ilia distanco.
La formulo de Neŭtono[redakti | redakti fonton]
Neŭtono en sia verko Principia Mathematica (1687) unue priskribis la leĝon de tiu fenomeno matematike. Laŭ li, la forto inter du mashavantaj objektoj estas
kie m1 kaj m2 estas la masoj de la objektoj, r la distanco inter la du objektoj (aŭ iliaj masocentroj) kaj G la gravita konstanto, G ≈ 6,67384 · 10−11 N · m2 · kg−2 laŭ mezurado[1]. Malgraŭ, ke iuj konsideras G kiel la kvara universala konstanto, ĝi estas la plej malprecize konata fizika konstanto.
Tio estis la unua fizika teorio, kiu aplikeblas en la astronomio, el kiu sekvis la leĝoj de Keplero, kiu permesis prognozojn pri la reveno de kometoj, kaj faris la dinamikon de la sunsistemo komprenebla.
En 1798 Henry Cavendish sukcesis eksperimente mezuri la denson de Tero, el kiu eblas kalkuli la gravitan konstanton G. Ne estas certe, ĉu tiun kalkulon li faris.
La ĝenerala teorio de relativeco[redakti | redakti fonton]

La gravitoteorio de Neŭtono estas limkazo (por malgrandaj rapidecoj kaj relative malgrandaj masoj) de la ĝenerala teorio pri relativeco de Albert Einstein (Ejnŝtejno)[2]. La lasta speciale gravas por la priskribo de la kosmo, ĉar por grandaj distancoj la gravito estas la dominanta forto.
La teorio pri relativeco konsideras graviton ne kiel forton, sed kiel econ de la spaco; laŭ ĝi masoj kurbigas la spacon ĉirkaŭ si tiel, ke aliaj masoj moviĝas ne laŭ rektaj vojoj, sed sekvas la kurbecon de la spaco. Dudimensia analogaĵo de tiu kurbiĝo estas streĉita elasta tuko, sur kiun oni metas pezan globon; ĝi tiam kurbigas la tukon, kaj aliaj globoj emus ruliĝi al la unua globo.
La diferenco inter la du teorioj, la neŭtona kaj la ejnŝtejna, estas sur Tero neglektebla. La ejnŝtejna teorio tamen estas la nura, kiu klarigas fenomenon malkovritan de astronomoj en la 19-a jarcento: la longa akso de la orbito de Merkuro ne havas konstantan direkton, sed turniĝas; do ĝia punkto plej proksima al la Suno, la perihelio, moviĝas ĉirkaŭ la Suno. Tiun fenomenon ne klarigas la neŭtona teorio; astronomoj tial unue kredis, ke ĝin kaŭzas nekonata planedo, nomata Vulkano.
Limoj de la nunaj teorioj[redakti | redakti fonton]
La ejnŝtejna teorio de relativeco estas, kvankam malsama al niaj ĉiutagaj spertoj, tute determina; ĝi permesas kalkuli el datenoj por iu tempo datenojn por alia (antaŭa aŭ posta) tempo. El la kvantuma fiziko oni tamen scias, ke almenaŭ en tre malgranda skalo la mondo ne estas determinisma; do la teorio de ĝenerala relativeco ne povas esti ĝusta je malgrandega skalo. Inverse la kvantuma fiziko ne konsideras la relativecon de rapidoj; do ĝi ne povas esti ĝusta je grandegaj rapidoj. Fizikistoj esperas trovi kvantum-gravitan teorion, kiu kunigas la du aspektojn.
Se la gravito estas priskribebla per iu kvantuma kampa teorio (kvantuma gravito), la gravitono (partiklo, kiu ĝis nun nur estas hipotezo) devas ekzisti. Tiam la gravitono rolas simile kiel la fotono en la elektromagneta interefiko.
Efiko de gravito[redakti | redakti fonton]
Baza fiziko[redakti | redakti fonton]
La gravito estas senkontakta interefiko, ekzemple la altiro inter Suno kaj Tero efikas tra la vakuo. Tiel ĝi similas al la elektromagneta interefiko, kiun (ĉar pli forta) oni jam povas rimarki en malgrandaĵoj (ekzemple magneto, elektra motoro, atomoj, molekuloj).
La gravito estas la plej malforta el la kvar fundamentaj fortoj, tamen por grandaj distancoj ĝi estas la sola efika forto, ĉar
- ĝi efikas, kvankam malpli kaj malpli forte, je ajna distanco (la forta kaj la malforta interagoj havas limigitan atingon);
- ĝi estas ŝirmata per nenio (elektra forto estas ŝirmebla per konduktanta materialo);
- la efikoj de la masoj nur adiciiĝas (ne ekzistas forpuŝa gravito, kiel ĉe elektra ŝargo).
Laŭ Neŭtono la gravito estas malproksima forto. Tio signifas, ke ŝanĝo en la fonto tuj efikas en la tuta spaco. Male, ŝanĝo en elektromagneta kampo disvastiĝas nur kun rapideco de lumo – temas pri proksima forto.
En la speciala teorio de relativeco, tuja disvastiĝo problemas pro la relativeco de samtempeco. Tial Albert Einstein formulis sian ĝeneralan teorion de relativeco, laŭ kiu la gravito kaŭzas kurbecon de la spacotempo, kiu disvastiĝas maksimume same rapide kiom la lumo.
Tajda forto[redakti | redakti fonton]
Ĉar la forto de gravito dependas de la distanco, ĝi malsame efikas al diversaj partoj de objekto. El tio rezultas tajda forto, kiu ricevis sian nomon de la regulaj leviĝo kaj malleviĝo de la surfaco de la oceanoj. Tiun moviĝon kaŭzas la fakto, ke la al-luna flanko de la Tero spertas pli fortan gravitan altiron ol la alia; la Luno fortiras la siaflankajn oceanojn de la Tero kaj la Teron de la aliflankaj oceanoj.
En iom granda objekto tajda forto povas esti konsiderinda kaj eĉ kaŭzi ĝian disiĝon. Ekzemple la kometo Shoemaker-Levy 9 en 1994 tre proksimiĝis al Jupitero kaj estis disŝirita de tajda forto. La marsa luno Fobo estas tiom proksima al Marso, ke ĝia propra gravito ne povus kunteni ĝin; ĝi kunteniĝas nur pro sia solida konsisto kaj diskrevus, se ĝi estus likva.
Gravito sur Tero[redakti | redakti fonton]

Sur Tero laŭ sia difino, la gravito sur la tera surfaco estas:
kie m estas la maso de objekto, MT la maso de la Tero kaj RT ties averaĝa radiuso.
De tiu formulo, oni deduktas la teran gravitan akcelon:
kiu valoras ĉirkaŭ 9,81 m/s². Ĝi tamen ne estas ĉie egala, pro tri kialoj:
- La Tero ne estas perfekta globo; ĝia radiuso estas ĉe la polusoj ĉ. 21 km malpli ol ĉe la ekvatoro. La ekvatoro havas pli grandan distancon al la tercentro, do malpli fortan graviton. La diferenco estas proksimume 0,25 %; pliaj 0,25 % rezultas el la fakto, ke ĉe la ekvatoro la centrifuga forto kompensas parton de la gravito.
- Ankaŭ je loka skalo la altoj de surteraj punktoj ne estas egalaj. Sur altaj montoj la gravito estas malpli forta ol sur marnivelo. Je alto de 10 km la gravito estas je 0,3 % malpli forta.
- La Tero havas ne ĉie la saman densecon. Rezulte en kelkaj lokoj la gravito povas esti je ĝis 0,5 % pli aŭ malpli forta ol en aliaj same altaj lokoj.
Lokaj masoj, ekzemple montoj, ordinare ne havas grandan influon al la gravita forto, sed povas influi ties direkton, kiu do ne ĉiam estas tiu al la tera centro. Grandaj montaroj, kiaj Himalajo aŭ la sudamerikaj kordileroj, ja kaŭzas pli grandan graviton.
Astronomio: Gravita lensado[redakti | redakti fonton]

La gravito de fora kosma objekto kutime estas tro malforta por rekta mezurado. Ĝi tamen kurbigas la spacon kaj tiel influas la lumon, kiu venas de steloj malantaŭ la objekto. Tiel eĉ povas esti, ke unu stelo aperas en du (proksimaj) lokoj sur la ĉielo. Se temas pri varianta stelo, povas esti, ke ĝi aperas en malsamaj statoj, ĉar la vojoj de la lumo estas malsame longaj.
Per gravita lensado eblas konkludi pri la pozicio de la lensanta objekto, kvankam ĝi estas malluma kaj ne rekte observebla.
Kvankam astronomoj jam antaŭe konsciis pri la eblo de gravita lensado (Ejnŝtejno priskribis ĝin en 1936), la unua efiko de tia lensado estis trovita nur en 1979, la "ĝemelaj kvazaroj", kiuj fakte estas nur unu kvazaro.
Gravita kampo[redakti | redakti fonton]
Gravita kampo estas fizika grando, aŭ skalara aŭ vektora, kiu estas funkcio de gravito laŭ loko kaj tempo.
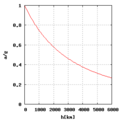
-
Vario de la gravita akcelo laŭ la altitudo (en km)
En Esperanto[redakti | redakti fonton]
Carlos Spínola en Veturado tra la interplaneda spaco[3] prezentas la sciencon, sur kiu baziĝas la movo en la spaco for de la tera surfaco. La amaskomunikiloj sufiĉe ofte parolas nun pri sendo de navigiloj al aliaj planedoj, satelitoj kaj apartaj lokoj en la sunsistemo por astronomiaj observado kaj esplorado, eĉ pri homaj vojaĝoj al Luno, Marso ktp. Sed la kutima sperto veturi sur Tero, eĉ aviadile, ne same funkcias en la spaco. Eblas profiti de la energio de la astroj mem. Por tion kompreni, necesas klarigi la signifon de la neŭtonaj leĝoj de la movo kaj de la universala gravito, kiuj gvidas la trajektoriojn de la falantaj kaj lanĉitaj objektoj sur la tera surfaco aŭ de la astroj en la sunsistemo. Per la neŭtonaj leĝoj eblas facile kalkuli la eskap-rapidon bezonatan por eliri de la tera surfaco aŭ de iu alia konata astro. La diversaj eblaj orbitoj en nia tera puto kaj iliaj trajtoj estos klarigitaj. Alia grava punkto estas kompreni kiel moviĝi energiŝpare inter orbitoj. Unue oni klarigas la ideon de la Hohmann-orbitoj. La kosmoŝipa motoro tute ne bezonas esti ĉiam funkcianta, sed nur en certaj mallongaj momentoj por ŝanĝi de unu orbito al alia. Nepras klarigo pri kiel atingi kinetan energion de la astroj mem per la metodo de gravita helpo (slingshot effect), kiu estas uzata por akceli aŭ bremsi la kosmoŝipojn. Por ekzemploj estas la interplanedaj vojaĝoj de la misio Rosetta de ESA kaj de la misio Cassini-Huygens de NASA-ESA. Tiu lasta celis al kaj esploris la saturnan satelitan sistemon dum preskaŭ 20 jaroj danke al la gravita helpo de Venuso, Tero, Jupitero kaj multfoje de la satelito Titano.
Vidu ankaŭ[redakti | redakti fonton]
- Fundamenta forto
- Gravita lensado
- Gravita serurtruo
- Leĝoj de Newton
- Neŭtona leĝo pri universala gravito
- Nigra truo
- Pezo
- Praeksplodo
Notoj[redakti | redakti fonton]
- ↑ CODATA Recommended Values (angle). National Institute of Standards and Technology. Alirita 2012-01-11.
- ↑ Albert Einstein . “Die Grundlagen der Allgemeinen Relativitätstheorie”, Annalen der Physik (la germana) 49 (4). Alirita 2013-01-13..
- ↑ Carlos Spínola, Veturado tra la interplaneda spaco. En IKU-libro de 2020, pp. 77-92.
Eksteraj ligiloj[redakti | redakti fonton]
- http://curious.astro.cornell.edu/question.php?number=310 (angle) Malsama pezo sur la polusoj ol sur la ekvatoro
- http://www.iac.es/ (hispane) Instituto de Astrofiziko de Kanarioj
- http://www.cliffrailwaylynton.co.uk (angle): Gravita funikularo, kiun pelas la pezo de akvo
- http://www.as.wvu.edu/coll03/phys/www/Heavisid.htm Arkivigite je 2006-04-22 per la retarkivo Wayback Machine (angle) Analogio inter gravito kaj elektromagnetismo