Kunfaldaĵo
En matematiko, kaj precipe en funkcionala analizo, kunfaldaĵo estas matematika operacio, kiu prenas du funkciojn f, g kaj produktas trian funkcion kiu, iusense, reprezentas la kvanton de superkuŝo inter f kaj inversigita kaj translaciita versio de g.
Tipe, en elektra inĝenierarto, la du funkcioj estas la impulsa reago de tempe nevaria lineara sistemo (nomita kerno), kaj la enigo en la sistemon. Tia kunfaldaĵo estas la sumo de la impulsaj reagoj pezigitaj laŭ la eniga amplitudo kaj rezultigas la eligon de la sistemo.
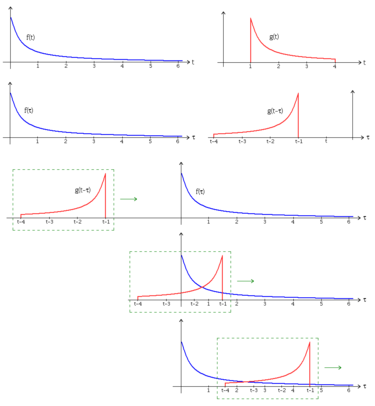
.
Difino[redakti | redakti fonton]
La kunfaldaĵon de kaj oni skribas jene: , per uzo de la signo . Ĝi estas difinita kiel la integraĵo de la produto de la du funkcioj kiam unu estas inversigita kaj translaciita. Tial ĝi estas specifa speco de integralaj transformoj:
La integraĵa amplekso dependas de la domajno en kiu la funkcioj estas difinitaj; ofte a = -∞ kaj b = +∞. Dum la simbolo estas uzata supre, ĝi ne devas reprezenti la domajnon tempan. Kaze de finita integraĵa amplekso, kaj ofte estas konsiderataj etendi periode en ambaŭ direktoj, por ke la termino ne implicu malobservi amplekson. Oni iam nomas tian uzadon de periodaj domajnoj cirkla kunfaldaĵo aŭ perioda kunfaldaĵo. Kompreneble etendigo per nuloj ankaŭ eblas. Uzi nul-etenditajn aŭ infinitajn domajnojn oni iam nomas linia kunfaldaĵo, precipe en la diskreta kazo sube.
Diskreta kunfaldaĵo[redakti | redakti fonton]
Por diskretaj funkcioj, oni povas uzi diskretan version de la kunfalda operacio. Ĝin donas
Kiam oni multiplikas du polinomojn, la koeficientojn de la produto donas la kunfaldaĵo de la originala koeficientaj sinsekvoj, en ĉi tiu senso (uzante etendojn kun nuloj, kiel menciite supre).
Por ĝeneraligi la suprajn kazojn, la kunfaldaĵo estas difinebla por ajnaj du integreblaj funkcioj difinitaj sur loke kompakta topologia grupo.
Alia ĝeneraligo estas la kunfaldaĵo de distribuoj.
Komputi diskretajn kunfaldaĵojn per la supra formulo rekte aplikata prenas Landau-notacion O(N2) aritmetikaj operacioj por N punktoj, sed tio estas reduktebla al O(N log N) per diversaj rapidaj algoritmoj.
Rapidaj kunfaldaj algoritmoj[redakti | redakti fonton]
Praktike, cifereca signal-prilaborado kaj aliaj aplikaĵoj de diskretaj kunfaldaĵoj tipe utiligas rapidajn kunfaldajn algoritmojn por pliigi la rapidon de la kunfaldaĵo al komplekseco O(N log N).
La plej oftaj rapidaj algoritmoj uzas rapidajn Fourier-transformojn (FFT) per la kunfalda teoremo: la cikla kunfaldaĵo de du sinsekvoj estas trovebla, se oni prenas FFT-on de ĉiu sinsekvo, multiplikas laŭpunkte, kaj faras inversan FFT-on. Neciklaj kunfaldaĵoj, ekzemple liniaj kunfaldaĵoj estas komputeblaj per cikla kunfaldaĵo uzanta nul-pakadon.
Ekzistas ankaŭ multaj aliaj rapidaj kunfaldaj algoritmoj kiuj ne uzas FFT-ojn mem, ekzemple numerteoriaj transformaj algoritmoj.









