Loka optimumo
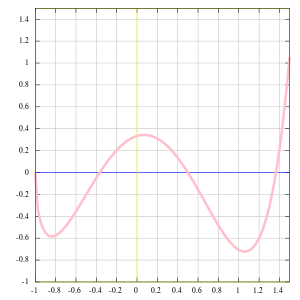
en intervalo [-1, 1,5].
Ĉi tie estas du lokaj optimumoj por x≈-0,8 kaj x≈1,1. La malloka optimumo estas nur unu el ili, x≈1,1
En aplika matematiko kaj komputiko, loka optimumo de optimumiga problemo estas solvaĵo kiu estas optimuma en najbara aro de solvaĵoj. Ĉi tiu estas en kontrasto al malloka optimumo, kiu estas la optimuma solvaĵo inter ĉiuj eblaj solvaĵoj.
La lokeco de la optimumo estas dependa de la najbaraĵa strukturo.
Multaj tiel nomataj solvaĵoj al tiaj optimumigaj problemoj estas trovoj de loka optimumo, kaj tial ili estas garantiitaj al trovi mallokan optimumon nur se la problemo havas nur unu lokan optimumon.

