Pluredra kombinaĵo
En geometrio, pluredra kombinaĵo estas kombinaĵo de kelkaj pluredroj kun komuna centro. Pluredra kombinaĵo estas la tri-dimensia analogo de du-dimensia stelo kun ne reciproke primaj nombroj de verticoj kaj la parametro de konekso ({6/2}, {8/2}, {9/3} ktp).

Najbaraj verticoj de kombinaĵo povas esti koneksigitaj al formo de konveksa pluredro kiu estas la konveksa koverto de la kombinaĵo. La kombinaĵo estas facetigo de sia konveksa koverto.
Alia konveksa pluredro estas formita per la malgranda centra spaco komuna al ĉiuj membroj de la kombinaĵo. Ĉi tiu pluredro povas esti la kerno por aro de steligoj inkluzivantaj ĉi tiun kombinaĵon. (Vidu en listo de pluredroj de Wenninger por ĉi tiuj kombinaĵoj kaj pliaj steligoj.)
Regulaj kombinaĵoj[redakti | redakti fonton]
Regula pluredra kombinaĵo povas esti difinita kiel kombinaĵo kiu, simile al regula pluredro, estas vertico-transitiva, latero-transitiva, kaj edro-transitiva. Kun ĉi tiu difino estas 5 regulaj kombinaĵoj.
| Nomo | Komponantoj | Bildo | Konveksa koverto | Kerno | Simetrio | Duala |
|---|---|---|---|---|---|---|
| Kombinaĵo de du kvaredroj aŭ stelokangulopluredro | Kvaredroj | 
|
Kubo | Okedro | Oh | Mem-duala |
| Kombinaĵo de kvin kvaredroj (nememspegulsimetria) | Kvaredroj | 
|
Dekduedro | Dudekedro | I | Mem-duala |
| Kombinaĵo de dek kvaredroj | Kvaredroj | 
|
Dekduedro | Dudekedro | Ih | Mem-duala |
| Kombinaĵo de kvin kuboj | Kuboj | Dekduedro | Romba tridekedro | Ih | Kombinaĵo de kvin okedroj | |
| Kombinaĵo de kvin okedroj | Okedroj | Dudek-dekduedro | Dudekedro | Ih | Kombinaĵo de kvin kuboj |
La plej bone sciata estas la kombinaĵo de du kvaredroj, la stelokangulopluredro, nomo estas donita al ĝi de Keplero. La verticoj de la du kvaredroj difinas kubon kaj la komunaĵo de ili estas okedro, kiu havas la samajn edrajn ebenojn kiel la kombinaĵo. Tial ĝi estas steligo de la okedro, kaj fakte, la sola finia steligo de okedro.
La stelokangulopluredro povas ankaŭ esti estimita kiel dualo-regula kombinaĵo.
La kombinaĵo de kvin kvaredroj estadas en du nememspegulsimetriaj versioj, kiu kune konsistigas la kombinaĵon de 10 kvaredroj. Ĉiu el la kvaredraj kombinaĵoj estas mem-duala, kaj la kombinaĵo de 5 kuboj estas duala al la kombinaĵo de 5 okedroj.
Dualo-regulaj kombinaĵoj[redakti | redakti fonton]
Dualo-regula kombinaĵo estas komponita el regula pluredro kaj ĝia duala, aranĝitaj reciproke ĉirkaŭ komuna intersfero aŭ mezosfero, tiel ke lateroj de unu pluredro sekcas la dualajn laterojn de la duala pluredro. Estas kvin ĉi tiaj kombinaĵoj.
La kubo-okedro kaj dekduedro-dudekedraj dualo-regulaj kombinaĵoj estas la unuaj steligoj de la kubokedro kaj dudek-dekduedro respektive.
La kombinaĵo de la malgranda steligita dekduedro kaj granda dekduedro aspektas de ekstero same kiel la malgranda steligita dekduedro, ĉar la granda dekduedro estas plene ene.
Uniformaj kombinaĵoj[redakti | redakti fonton]
Unuforma pluredra kombinaĵo estas vertico-transitiva kombinaĵo de unuformaj pluredroj.
En 1976 John Skilling publikigis liston en kiu li numerigis 75 kombinaĵojn (inkluzivante de 6 kiel malfiniaj prismaj aroj de kombinaĵoj, №20 ... №25) faritaj de unuformaj pluredroj kun turna simetrio. Ĉi tiu listo inkluzivas la 5 regulajn kombinaĵojn.
- 1 ... 19: diversaj (4, 5, 6, 9, 17 estas la 5 regulaj kombinaĵoj)
 UC1 |
 UC2 |
 UC3 |
 UC4 |
 UC5 |
 UC6 |
 UC7 |
 UC8 |
 UC9 |
 UC10 |
 UC11 |
 UC12 |
 UC13 |
 UC14 |
 UC15 |
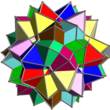 UC16 |
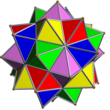 UC17 |
 UC18 |
 UC19 |
- 20 ... 25: prisma simetrio enigita en prisman simetrion
 UC20 |
 UC21 |
 UC22 |
 UC23 |
 UC24 |
 UC25 |
- 26 ... 45: prisma simetrio enigita en okedran aŭ dudekedran simetrion
 UC26 |
 UC27 |
 UC28 |
 UC29 |
 UC30 |
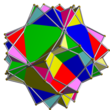 UC31 |
 UC32 |
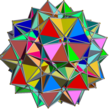 UC33 |
 UC34 |
 UC35 |
 UC36 |
 UC37 |
 UC38 |
 UC39 |
 UC4 |
 UC41 |
 UC42 |
 UC43 |
 UC44 |
 UC45 |
- 46 ... 67: kvaredra simetrio enigita en okedran aŭ dudekedran simetrion
 UC46 |
 UC47 |
 UC48 |
 UC49 |
 UC50 |
 UC51 |
 UC52 |
 UC53 |
 UC54 |
 UC55 |
 UC56 |
 UC57 |
 UC58 |
 UC59 |
 UC60 |
 UC61 |
 UC62 |
 UC63 |
 UC64 |
 UC65 |
 UC66 |
 UC67 |
- 68 ... 75: paroj de nememspegulsimetriaj
 UC68 |
 UC69 |
 UC70 |
 UC71 |
 UC72 |
 UC73 |
 UC74 |
 UC75 |
Vidu ankaŭ[redakti | redakti fonton]
- Unuforma pluredra kombinaĵo
- Pluredro
- Kahelaro (geometrio)
- Malfinioedro aŭ malfinia pluredro
- Hiperpluredro
- Regula hiperpluredro
- Listo de regulaj hiperpluredroj, ankaŭ kun listo de regulaj kahelaroj
Eksteraj ligiloj[redakti | redakti fonton]
- Pluredra kombinaĵo je MathWorld
- Pluredra kombinaĵo je Virtualaj Realaj Pluredroj
- Unuformaj kombinaĵoj de unuformaj pluredroj
- 75 Unuformaj kombinaĵoj de unuformaj pluredroj de John Skilling Arkivigite je 2007-09-28 per Archive.today
- Unuformaj kombinaĵoj de unuformaj pluredroj de John Skilling
- Pluredraj kombinaĵoj Arkivigite je 2007-01-02 per la retarkivo Wayback Machine
- [1] Arkivigite je 2009-10-19 per la retarkivo Wayback Machine
- [2]
- Kombinaĵo de malgranda steligita dekduedro kaj granda dekduedro {5/2,5}+{5,5/2}
- [3] Michael G. Harman, Pluredraj kombinaĵoj, nepublikigita manuskripto, proksimume 1974.
Referencoj[redakti | redakti fonton]
- John Skilling, Uniform Compounds of Uniform Polyhedra - Unuformaj Kombinaĵoj de Unuformaj Pluredroj, Mathematical Proceedings of the Cambridge Philosophical Society - Matematikaj Paperoj de la Kembriĝa Filozofia Socio, Volumo. 79, pp. 447–457, 1976.

