Rektigo (geometrio)

Rektigita kubo estas kubokedro - randoj reduktiĝis al verticoj, kaj verticoj elvolvis novajn edrojn

Durektigita kubo estas okedro - edroj estas reduktita al punktoj kaj novaj edroj estas centrita sur la originalaj verticoj.

Rektigita kuba kahelaro - randoj reduktis al verticoj, kaj verticoj elvolvis novajn ĉelojn.

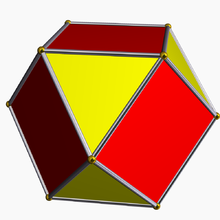
En eŭklida geometrio, rektigo estas la procezo de senpintigado de hiperpluredro per markado de la mezpunktoj de ĉiuj ĝiaj lateroj, kaj tranĉado for de ĝiaj verticoj je tiuj punktoj. La rezultanta hiperpluredro estas barita per la verticaj figuroj kaj la rektigitaj facetoj de la originala hiperpluredro.

Rektigo kiel fina tranĉo de randoj

Rektigo estas la fina punkto de tranĉa procezo. Ekzemple sur kubo ĉi tiu vico montras kvar ŝtupojn de de tranĉado inter la regula kaj rektigita formoj:

Rektigo de pli alta ordo povas esti plenumita sur regulaj hiperpluredroj de pli altaj dimensioj. Rektigo de la plej alta ordo kreas la dualan hiperpluredron. Rektigo senpintigas randoj al punktoj. Durektigo senpintigas edroj al punktoj. Trirektigo senpintigas ĉeloj al punktoj.

Ekzemplo de durektigo kiel fina tranĉo al edro

Ĉi tiu vico montras durektigitan kubon kiel la finon de vico de kubo al ĝia duala okedro kie la originalaj edroj estas senpintigitaj ĉiu al sola punkto:

En plurlateroj

La duala de plurlatero estas la samo kiel ĝia rektigita formo.

En pluredroj kaj ebenaj kahelaroj

Ĉiu platona solido kaj ĝia duala havas la saman rektigita pluredro. (Ĉi tio ne estas vero por hiperpluredroj en pli altaj dimensioj.)

La rektigita pluredro estas esprimebla kiel la komunaĵo de la originala platona solido kun vere skalita samcentra versio de ĝia dualo. Por ĉi tio, ĝia nomo estas kombinaĵo de la nomoj de la originala kaj la duala:

1. Rektigita kvaredro, kies duala estas la kvaredro, estas la kvar-kvaredro, pli bona sciata kiel la okedro.
2. Rektigita okedro, kies duala estas la kubo, estas la kubokedro.
3. Rektigita dudekedro, kies duala estas la dekduedro, estas la dudek-dekduedro.
4. Rektigita kvadrata kahelaro estas kvadrata kahelaro.
5. Rektigita triangula kahelaro aŭ seslatera kahelaro estas tri-seslatera kahelaro.

Ekzemploj

Familio	Gepatro	Rektigo	Duala
[3,3]	Kvaredro	Kvar-kvaredro	Kvaredro
[4,3]	Kubo	Kubokedro	Okedro
[5,3]	Dekduedro	Dudek-dekduedro	Dudekedro
[6,3]	Seslatera kahelaro	Tri-seslatera kahelaro	Triangula kahelaro
[7,3]	Ordo-3 seplatera kahelaro	Tri-seplatera kahelaro	Ordo-7 triangula kahelaro
[4,4]	Kvadrata kahelaro	Kvadrata kahelaro	Kvadrata kahelaro
[5,4]	Ordo-4 kvinlatera kahelaro	Kvar-kvinlatera kahelaro	Ordo-5 kvadrata kahelaro

En plurĉeloj kaj 3-kahelaroj

Ĉiu konveksa regula plurĉelo havas rektigitan formon kiu estas uniforma plurĉelo.

Regula plurĉelo {p,q,r} havas ĉelojn {p,q}. Ĝia rektigo havas du ĉelajn specoj, rektigitaj {p,q} pluredroj restas de la originalaj ĉeloj kaj {q,r} pluredroj estas novaj ĉeloj formitaj de la senpintigitaj verticoj.

Rektigita {p,q,r} estas ne la sama kiel rektigita {r,q,p}, tamen. Plua tranĉo, nomata kiel dutranĉo, estas simetria inter plurĉelo kaj ĝia dualo.

Ekzemploj

Familio	Gepatro	Rektigo	Durektigo (Duala de rektigo)	Trirektigo (Duala)
[3,3,3]	5-ĉelo	Rektigita 5-ĉelo	Rektigita 5-ĉelo	5-ĉelo
[4,3,3]	4-hiperkubo	Rektigita 4-hiperkubo	Rektigita 16-ĉelo (24-ĉelo)	16-ĉelo
[3,4,3]	24-ĉelo	Rektigita 24-ĉelo	Rektigita 24-ĉelo	24-ĉelo
[5,3,3]	120-ĉelo	Rektigita 120-ĉelo	Rektigita 600-ĉelo	600-ĉelo
[4,3,4]	Kuba kahelaro	Rektigita kuba kahelaro	Rektigita kuba kahelaro	Kuba kahelaro
[5,3,4]	Ordo-4 dekduedra kahelaro	Rektigita ordo-4 dekduedra kahelaro	Rektigita ordo-5 kuba kahelaro	Ordo-5 kuba kahelaro

Ordoj de rektigo

Unua orda rektigo senpintigas lateroj al punktoj. Se la hiperpluredro estas regula, ĉi tiu formo estas prezentita per etendita notacio de simbolo de Schläfli t₁{p,q,...}.

Dua orda rektigo, aŭ durektigo, senpintigas edrojn al punktoj. Se la hiperpluredro estas regula, ĝi havas notacion t₂{p,q,...}. Por pluredroj, durektigo kreas dualan pluredron.

Pli alta ordo rektigoj povas esti konstruita por pli altaj dimensioj de hiperpluredroj. Ĝenerale n-rektigo senpintigas n-hiperedroj al punktoj.

Se n-hiperpluredro estas (n-1)-rektigita, ĝiaj facetoj estas reduktitaj al punktoj kaj la hiperpluredro iĝas sian dualon.

Notacioj kaj facetoj

Ekzistas malsamaj ekvivalentaj notacioj por ĉiu ordo de rektigo. Ĉi tiuj tabeloj montras la nomojn per dimensio kaj la du specojn de facetoj por ĉiu.

Regulaj plurlateroj

Facetoj estas randoj, prezentis kiel {2}.

nomo {p}	Coxeter-Dynkin	t-notacia simbolo de Schläfli	Vertikala simbolo de Schläfli
			Nomo	Faceto-1	Faceto-2
Gepatro		t0{p}	${\begin{Bmatrix}p\end{Bmatrix}}$	${\begin{Bmatrix}2\end{Bmatrix}}$
Rektigita		t1{p}	${\begin{Bmatrix}p\end{Bmatrix}}$		${\begin{Bmatrix}2\end{Bmatrix}}$

Regulaj pluredroj kaj kahelaroj

Facetoj estas regulaj plurlateroj.

nomo {p,q}	Coxeter-Dynkin	t-notacia simbolo de Schläfli	Vertikala simbolo de Schläfli
			Nomo	Faceto-1	Faceto-2
Gepatro		t0{p,q}	${\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\end{Bmatrix}}$
Rektigita		t1{p,q}	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	${\begin{Bmatrix}p\end{Bmatrix}}$	${\begin{Bmatrix}q\end{Bmatrix}}$
Durektigita		t2{p,q}	${\begin{Bmatrix}q,p\end{Bmatrix}}$		${\begin{Bmatrix}q\end{Bmatrix}}$

Regulaj plurĉeloj kaj kahelaroj

Facetoj estas regulaj aŭ rektigitaj pluredroj.

nomo {p,q,r}	Coxeter-Dynkin	t-notacia simbolo de Schläfli	Vertikala simbolo de Schläfli
			Nomo	Faceto-1	Faceto-2
Gepatro		t0{p,q,r}	${\begin{Bmatrix}p,q,r\end{Bmatrix}}$	${\begin{Bmatrix}p,q\end{Bmatrix}}$
Rektigita		t1{p,q,r}	${\begin{Bmatrix}p\\q,r\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	${\begin{Bmatrix}q,r\end{Bmatrix}}$
Durektigita		t2{p,q,r}	${\begin{Bmatrix}q,p\\r\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q\\r\end{Bmatrix}}$
Trirektigita		t3{p,q,r}	${\begin{Bmatrix}r,q,p\end{Bmatrix}}$		${\begin{Bmatrix}r,q\end{Bmatrix}}$

Regulaj 5-hiperpluredroj kaj 4-kahelaroj

Facetoj estas regulaj aŭ rektigitaj plurĉeloj.

nomo {p,q,r,s}	Coxeter-Dynkin	t-notacia simbolo de Schläfli	Vertikala simbolo de Schläfli
			Nomo	Faceto-1	Faceto-2
Gepatro		t0{p,q,r,s}	${\begin{Bmatrix}p,q,r,s\end{Bmatrix}}$	${\begin{Bmatrix}p,q,r\end{Bmatrix}}$
Rektigita		t1{p,q,r,s}	${\begin{Bmatrix}p\\q,r,s\end{Bmatrix}}$	${\begin{Bmatrix}p\\q,r\end{Bmatrix}}$	${\begin{Bmatrix}q,r,s\end{Bmatrix}}$
Durektigita		t2{p,q,r,s}	${\begin{Bmatrix}q,p\\r,s\end{Bmatrix}}$	${\begin{Bmatrix}p,q\\r\end{Bmatrix}}$	${\begin{Bmatrix}q\\r,s\end{Bmatrix}}$
Trirektigita		t3{p,q,r,s}	${\begin{Bmatrix}r,q,p\\s\end{Bmatrix}}$	${\begin{Bmatrix}r,q,p\end{Bmatrix}}$	${\begin{Bmatrix}r,q\\s\end{Bmatrix}}$
Kvarrektigita		t4{p,q,r,s}	${\begin{Bmatrix}s,r,q,p\end{Bmatrix}}$		${\begin{Bmatrix}s,r,q\end{Bmatrix}}$

Vidu ankaŭ

• Operacioj je hiperpluredroj kaj kahelaroj:
  • Tranĉo t_{0, 1}{p, ...}
  • Laterotranĉo t_{0, 2}{p, q, ...}
  • Lateroverticotranĉo t_{0, 1, 2}{p, q, ...}
  • Edrotranĉo t_{0, 3}{p, q, r, ...}
  • Edroverticotranĉo t_{0, 1, 3}{p, q, r, ...}
  • Edrolaterotranĉo t_{0, 2, 3}{p, q, r, ...}
  • Edrolateroverticotranĉo t_{0, 1, 2, 3}{p, q, r, ...}
  • Ĉelotranĉo t_{0, 4}{p, q, r, s, ...}
  • Entutotranĉo t_{0, 1, ..., n-1}{p₁, p₂, ..., p_n-1}
  • Rektigo t₁{p, ...}
  • Dutranĉo t_{1, 2}{p, q, ...}
  • Alternado
  • Riproĉigo
• Simbolo de Schläfli - etendita simbolo de Schläfli priskribas rezultojn de la operacioj faritaj je regulaj hiperpluredroj kaj regulaj kahelaroj

• Duala hiperpluredro
• Kvazaŭregula pluredro
• Listo de regulaj hiperpluredroj
• Tranĉo (geometrio)
• Pluredra notacio de Conway

Referencoj

• Coxeter, H.S.M. Regulaj hiperpluredroj, (3-a redakcio, 1973), Dovera redakcio, ISBN 0-486-61480-8 (pp. 145–154 Ĉapitro 8: Tranĉo)

Eksteraj ligiloj

• Eric W. Weisstein, Rektigo en MathWorld.
• George Olshevsky, Rektigo en Glossary for Hyperspace.