Pakada problemo
Pakadaj problemoj estas speco de problemoj en matematiko.
En pakada problemo estas donitaj:
- unu aŭ pli multaj (kutime du-dimensiaj aŭ tri-dimensiaj) konteneroj;
- kelkaj 'varoj', iuj aŭ ĉiuj el kiuj devas esti pakitaj en ĉi tiujn kontenerojn.

Kutime la pakado devas esti sen breĉoj aŭ interkovroj, sed en iuj pakadaj problemoj la interkovroj (de varoj unu la alian aŭ kun la rando de la kontenero estas permesita sed devus esti farita kiel eblas pli malgranda. En la aliaj, breĉoj estas permesitaj, sed interkovroj estas ne permesitaj, kutime la tuteca areo de breĉoj devus esti farita kiel eblas pli malgranda.
Kutime la problemoj engaĝas trovadon de la maksimuma kvanto de certaj formoj kiuj povas esti pakitaj, aŭ trovadon de la minimuma amplekso de la kontenero.
Eĉ se iu pakado estas la plej densa ebla, iam okazas ke iu el la pakitaj eroj havas liberecon de movo en iu regiono.
Pakado de malfinia spaco[redakti | redakti fonton]
Multaj el ĉi tiuj problemoj, se la kontenera amplekso estas pligrandigita en ĉiuj direktoj, iĝas ekvivalento al la problemo de pakado de objektoj kiel eblas dense en malfinia eŭklida spaco. La keplera konjekto statis la optimalan solvaĵon por pakado de sferoj, poste ĝi estis pruvita de Hales.
Cirkloj en ebeno[redakti | redakti fonton]


Cirkloj (n-sferoj en aliaj dimensioj) ne povas esti pakitaj kun 100% uzo de spaco en dimensioj pli grandaj ol unu (en unu-dimensia spaco, cirklo nur konsistas el du punktoj). Tio estas, tie ĉiam estas neuzata spaco se oni pakas nur cirklojn. La plej kompetenta vojo de pakado cirkloj, seslatera pakado, havas relativan uzadon de la spaco . La kvadrata pakado estas malpli densa, kaj havas relativan uzadon de la spaco
Sferoj en eŭklida pilko[redakti | redakti fonton]
La problemo de trovanta de la plej malgranda pilko tia ke k disaj malfermitaj unuoblaj pilkoj povas esti pakitaj en ĝin havas simplan kaj plenan respondo en n-dimensia eŭklida spaco se k≤n+1, kaj en malfinio-dimensia hilberta spaco sen limigoj. En ĉi tiu okazo, konfiguro de k poduope tanĝantaj unuoblaj pilkoj estas havebla. Estu la centroj je la verticoj a1, ..., ak de regula (k-1)-dimensia simplaĵo kun longo de latero egala al 2. La distanco de ĉiu vertico de la centro de la simplaĵo estas . Ankaŭ, ĉiu la alia punkto de la spaco bezone havas pli grandan distancon de almenaŭ unu el la k verticoj. Tiel, la k malfermitaj unuoblaj pilkoj centritaj je a1, ..., ak estas inkluzivitaj en pilkon de radiuso , kiu estas minimuma por ĉi tiu konfiguro.
Sferoj en briko[redakti | redakti fonton]
Klasika problemo estas la sfera pakanta problemo, kiu estas trovado de kvanto de sferaj objektoj de donita diametro d kiuj povas esti pakitaj en brikon de donita amplekso a×b×c.
Cirkloj[redakti | redakti fonton]
Estas multaj problemoj engaĝaj pakadon de cirkloj en apartan formon de la plej malgranda ebla amplekso. Noto ke ĉi tiuj problemoj estas matematike malsamaj de la ideoj en la cirkla pakanta teoremo.
Cirkloj en cirklo[redakti | redakti fonton]
Iu el la ne-bagatelaj cirklaj pakadaj problemoj estas pakado de unuoblaj cirkloj en la kiel eblas plej malgrandan cirklon.
Minimumaj solvaĵoj:
Cirkloj en kvadrato[redakti | redakti fonton]
Paki n unuoblajn cirklojn en la kiel eblas plej malgrandan kvadraton. Ĉi tio estas proksime rilatanta al disvastigo de punktoj en unuobla kvadrato kun trovado de la plej granda minimuma apartigo dn inter la punktoj. Por konverti inter ĉi tiuj du formulaĵoj de la problemo, la kvadrata latero L por n unuoblaj cirkloj estas L=2+2/dn.
Aktualaj plej bonaj solvaĵoj:
* indikas ke la solvaĵo estas sciata al esti optimala.
Cirkloj en izocela orta triangulo[redakti | redakti fonton]
Paki n unuoblajn cirklojn en la kiel eblas plej malgrandan izocelan ortan triangulon - ortan triangulon kun anguloj 45°, 45°, 90°.
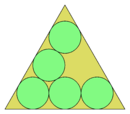
Cirkloj en egallatera triangulo[redakti | redakti fonton]
Paki n unuoblajn cirklojn en la kiel eblas plej malgrandan egallateran triangulon.
Minimumaj solvaĵoj:
Cirkloj en regula seslatero[redakti | redakti fonton]
Paki n unuoblajn cirklojn en la kiel eblas plej malgrandan regula seslateron.
| Kvanto de unuoblaj cirkloj n | Latero de la kontenera seslatero |
|---|---|
| 1 | ≈1,154 |
| 2 | ≈2,154 |
| 3 | ≈2,309 |
| 4 | ≈2,666 |
| 5 | ≈2,999 |
| 6 | ≈3,154 |
| 7 | ≈3,154 |
| 8 | ≈3,709 |
| 9 | ≈4,011 |
| 10 | ≈4,119 |
| 11 | ≈4,309 |
| 12 | ≈4,309 |
| 13 | ≈4,618 |
| 14 | ≈4,666 |
| 15 | ≈4,961 |
Kvadratoj[redakti | redakti fonton]
Kvadratoj en kvadrato[redakti | redakti fonton]
Problemo estas la kvadrata pakada problemo, kie oni devas difini kiun kvanton da kvadratoj de latero 1 oni povas paki en kvadraton de latero a. Evidente, se a estas entjero, la respondo estas a2, sed la preciza, aŭ eĉ asimptota, kvanto de malŝparata spaco por ne-entjera a estas ne sciata.
Pruvitaj minimumaj solvaĵoj:
| Kvanto de kvadratoj | Latero de la kontenera kvadrato | |
|---|---|---|
| 1 | 1 | |
| 2 | 2 | |
| 3 | 2 | |
| 4 | 2 | |
| 5 | 2+2-1/2≈2,707 | 
|
| 6 | 3 | |
| 7 | 3 | 
|
| 8 | 3 | |
| 9 | 3 | |
| 10 | 3+2-1/2≈3,707 | 
|
Aliaj rezultoj:
- Se eblas paki n2-2 kvadratoj en kvadraton de latero a, tiam a≥n.
- La naiva maniero (latero al latero) malŝparas spacon malpli ol 2a+1.
- La malŝparata spaco estas asimptote o(a7/11).
- La malŝparata spaco ne estas asimptote o(a1/2).
- 11 unuoblaj kvadratoj ne povas esti pakitaj en kvadraton de latero malpli granda ol .
Kvadratoj en cirklo[redakti | redakti fonton]
Paki n kvadratojn en la kiel eblas plej malgrandan cirklon.
Minimumaj solvaĵoj:
| Kvanto de kvadratoj | Radiuso de la kontenera cirklo | |
|---|---|---|
| 1 | 2-1/2 ≈0,707 | |
| 2 | ≈1,118 | |
| 3 | ≈1,288 | |
| 4 | ≈1,414 | |
| 5 | ≈1,581 | 
|
| 6 | ≈1,688 | 
|
| 7 | ≈1,802 | |
| 8 | ≈1,978 | |
| 9 | ≈2,077 | |
| 10 | ≈2,121 | |
| 11 | ≈2,215 | |
| 12 | ≈2,236 |
Kahelaroj[redakti | redakti fonton]
En kahelaroj, devas esti nek breĉoj, nek interkovroj.
Ortanguloj en ortangulo[redakti | redakti fonton]
Estas gravaj teoremoj pri kahelado de ortanguloj (kaj kubsimilaĵoj) en ortanguloj (kubsimilaĵoj) sen breĉoj aŭ interkovroj:
- Teoremo de Klarner: a×b ortangulo povas esti pakita kun 1 × n ortangulo se kaj nur se n estas divizoro de a aŭ n estas divizoro de b.
- Teoremo de de Bruijn: Skatolo povas esti pakita kun harmonaj brikoj a×ab×abc se la skatolo havas dimensioj ap×abq×abcr por iuj naturaj nombroj p, q, r, kio estas ke la skatolo estas entjera oblo de la briko je ĉiu dimensio.
Plurkvadratetoj[redakti | redakti fonton]

La studo de kahelaroj plurkvadratetoj grande koncernas du klasojn de problemoj: kaheli ortangulon kun kongruaj kaheloj, kaj al paki po unu el ĉiu n-kvadrateto en ortangulon.
Klasika enigmo de la dua speco estas al aranĝi ĉiujn 12 malsamajn 5-kvadratetojn en ortangulojn 3×20, 4×15, 5×12 kaj 6×10.
Vidu ankaŭ[redakti | redakti fonton]
- Pakado de aro
- Uja pakanta problemo
- Enigmo de Slothouber-Graatsma
- Enigmo de Conway
- Tetriso
- Kovrada problemo
- Dorssakproblemo
- Kvaredra pakado
- Problemo pri tranĉado de stoko
- Problemo pri kvanto de tuŝoj
Eksteraj ligiloj[redakti | redakti fonton]
- Eric W. Weisstein, Pakado en MathWorld.
- Eric W. Weisstein, Pakado de kvadratoj en MathWorld.
- Eric W. Weisstein, Pakado de cirkloj en MathWorld.
- Eric W. Weisstein, Teoremo de Klarner en MathWorld.
- Eric W. Weisstein, Teoremo de de Bruijn en MathWorld.
- Pakada centro de Erich Arkivigite je 2010-03-14 per la retarkivo Wayback Machine
- "Skatola pakado" de Jr. Ed Pegg.
- Erich Friedman, "Pakado de unuoblaj kvadratoj en kvadratojn: katastro kaj novaj rezultoj" Arkivigite je 2009-07-27 per la retarkivo Wayback Machine, La Elektronika Ĵurnalo de Kombinatoriko DS7 (2005).
- M. Kearney kaj P. Shiu, "Kompetenta pakado de unuoblaj kvadratoj en kvadraton", La Elektronika Ĵurnalo de Kombinatoriko 9:1 #R14 (2002).
- P. Erdős kaj R. L. Graham, "Pri pakado de kvadratoj kun egalaj kvadratoj"[rompita ligilo], Ĵurnalo de Kombina Teorio, Serio A 19 (1975), pp. 119–123.
- W. Stromquist, "Pakado de 10 aŭ 11 unuoblaj kvadratoj en kvadrato", La Elektronika Ĵurnalo de Kombinatoriko 10 #R8 (2003).
- Wagon, Stan (aŭgusto-septembro 1987). Fourteen Proofs of a Result About Tiling a Rectangle - Dek kvar pruvoj de rezultoj pri kahelado de ortangulo. The American Mathematical Monthly - La Amerika Matematiko Monate 94 (7) 601-617. Kontrolita en 6 januaro 2010.