Momanto (statistiko)

En statistiko, la momantoj estas mezuroj de distribua funkcio de hazarda variablo. Ili kongruas al la parametroj de la priskriba statistiko.

La momanto de grado k>0 pri hazarda variablo X estas, se ekzistas, la atendata valoro de X^k , t.e. : $m_{k}=\operatorname {E} [X^{k}]\ .$

Centraj momantoj

Centra momanto de grado $k\geq 0$ pri hazarda variablo X estas la nombro $\mu _{k}=\operatorname {E} [\left(X-\operatorname {E} [X]\right)^{k}]\ .$

La 0-a centra momanto $\mu _{0}\$ egalas al 1, dum la 1-a centra momanto $\mu _{1}\$ egalas al 0.

Rimarkindaj momantoj

Pozitiva asimetriokoeficiento V

Negativa asimetriokoeficiento V

Kurtosisojn $\gamma _{2}$ pri malsamaj probablodensaj funkcioj, sed kun sama varianco; la nigra kurbo estas la normala distribuo.

Iaj momantoj estas konitaj per apartaj nomoj. Ili estas kutime uzataj por karakterizi hazardan variablon.

• La unua momanto de variablo: $m_{1}=\operatorname {E} [X]$ , ofte notata $\mu \$ aŭ iam $m\$, simple kongruas al la atendita valoro.

• La dua centra momanto: $\mu _{2}=\operatorname {E} [(X-\mu )^{2}]$, ofte notata $\sigma ^{2}\$, $\sigma _{X}^{2}$, $\operatorname {var} (X)$, kongruas al la varianco.

• La tria norma centra momanto: $\gamma _{1}={\frac {\mu _{3}}{\sigma ^{3}}}=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{3}\right]\$, kongruas al la asimetriokoeficiento. Ĝi permesas mezuri asimetrion de probablodistribuo, kaj estas pozitiva aŭ negativa; evidente, ĝi nulas pri (simetria) normala distribuo.

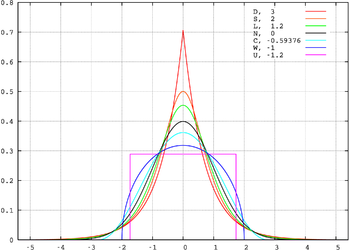
• La kvara norma centra momanto : $\beta _{2}={\frac {\mu _{4}}{\sigma ^{4}}}=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]\,$ kongruas al la kurtosiso (el greka termino, kiu signifas ŝvelo). Ĝi permesas mezuri diferencojn inter distribuokurboj; akra pinto kun longa vosto havas grandan kurtosison, aŭ runda supro kun mallonga vosto havas malgrandan kurtosison. Pri normala distribuo $\beta _{2}=3$, tial ke oni foje konsideras $\gamma _{2}={\frac {\mu _{4}}{\sigma ^{4}}}-3$, kiu estas aŭ pozitiva (granda kurtosiso), aŭ negativa (malgranda kurtosiso), aŭ nula ("kvazaŭ" normala distribuo).

Rilatoj inter ordinaraj kaj centraj momantoj

Oni povas skribi rilatojn inter la ordinaraj momantoj $m_{k}$ kaj la centraj momantoj $\mu _{k}$ . Sekvas ekzemploj ĝis k=4:

$\mu _{2}=m_{2}-m_{1}^{2}\,,$

$\mu _{3}=m_{3}-3\,m_{1}\,m_{2}+2\,m_{1}^{3}\,,$

$\mu _{4}=m_{4}-4\,m_{1}\,m_{3}+6\,m_{1}^{2}\,m_{2}-3m_{1}^{4}\,;$

kaj

$m_{2}=\mu _{2}+m_{1}^{2}\,,$

$m_{3}=\mu _{3}+3\,m_{1}\mu _{2}+m_{1}^{3}\,,$

$m_{4}=\mu _{4}+4\,m_{1}\mu _{3}+6\,m_{1}^{2}\mu _{2}+m_{1}^{4}\,.$

Vidu ankaŭ

• Momanto