Staranta onda rilatumo

En telekomunikado, staranta onda rilatumo estas la rilatumo de la amplitudo de parta staranta ondo je malnodo (maksimumo) al la amplitudo je najbara vertico (minimumo), en elektra tradona linio.

La staranta onda rilatumo estas kutime difinita kiel rilatumo de elektraj tensiaj kaj nomata kiel tensia staranta onda rilatumo.

Ekzemple, la valoro 1,2 de staranta onda rilatumo signifas ke maksimuma onda amplitudo estas je 1,2 fojoj pli granda ol la minimuma onda amplitudo.

Ankaŭ eblas difini la starantan ondan rilatumon por elektra kurento, kiu havas la saman nombran valoro.

La staranta onda rilatumo povas ankaŭ esti difinita kiel la rilatumo de la maksimuma amplitudo de la elektra kampa forteco al ĝia minimuma amplitudo.

La povuma staranta onda rilatumo egalas al kvadrato de la tensia staranta onda rilatumo.

Interrilato al la reflekta koeficiento

La elektra tensia komponanto de staranta ondo en uniforma tradona linio konsistas el la antaŭena ondo (kun kompleksa valoro V_a) kune kun la reflektita ondo (kun kompleksa valoro V_r).

Reflektoj okazas pro nekontinuecoj, kiel neperfekteco en aliloke uniforma tradona linio, aŭ se tradona linio estas finita per impedanco ne egala al ĝia karakteriza impedanco. La reflekta koeficiento Γ estas difinita tiel ke

$\Gamma ={\frac {V_{r}}{V_{a}}}$

Γ estas kompleksa nombro kiu priskribas ambaŭ la grandecon kaj la fazan ŝovon de la reflekto. La plej simplaj okazoj estas:

• Γ = -1: maksimuma negativa reflekto, se la linio estas mallongo-cirkvita,
• Γ = 0: neniu reflekto, se la linio estas perfekte kongruigita,
• Γ = 1: maksimuma pozitiva reflekto, se la linio estas malfermito-cirkvita.

Por la kalkulo de staranta onda rilatumo, nur la grandeco de Γ, signifita per ρ = |Γ|, estas grava. Ĝi estas egala al la rilatumo de amplitudoj de la ondoj:

$\rho ={\frac {|V_{r}|}{|V_{a}|}}$

Je iuj punktoj laŭ la linio la du ondoj interferas konstrue, kaj la rezultanta amplitudo V_max estas sumo de ilia amplitudoj:

$V_{max}=V_{a}+V_{r}=V_{a}+\rho V_{a}=V_{a}(1+\rho )$

Je aliaj punktoj, la ondoj interferas detrue, kaj la rezultanta amplitudo V_min estas la diferenco inter ilia amplitudoj:

$V_{min}=V_{a}-V_{r}=V_{a}-\rho V_{a}=V_{a}(1-\rho )$

La tensia staranta onda rilatumo K estas do

$K={\frac {V_{max}}{V_{min}}}={\frac {1+\rho }{1-\rho }}$

Pro tio ke ρ ĉiam estas en la limigoj [0, 1], do ĉiam K≥1.

Momenta tensio

Parte staranta ondo por kelkaj ρ. Ĉi tie A=1 kaj k=1. La maksimumo kaj minimumo de V_mot en ĉiu periodo estas V_max kaj V_min respektive, kaj ilia rilatumo estas la staranta onda rilatumo. La grafikaĵo montras ne la momentan elektran tension laŭ la tradona linio je iu tempo, sed la amplitudon de la oscilado je ĉiu punkto.

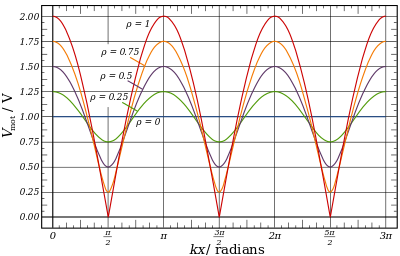
Elektra tensio de antaŭena ondo kiel funkcio de tempo t kaj de distanco x laŭ la tradona linio estas

$V_{a}(x,t)=A\sin(\omega t-kx)$

kie A estas la amplitudo de la antaŭena ondo;

ω estas ĝia angula frekvenco;

k estas la onda nombro, egala al ω dividita per la rapido de la ondo.

La elektra tensio de la reflektita ondo estas simila funkcio, sed kun signumo de x inversigita kaj malamplifita per la reflekta koeficiento ρ:

$V_{r}(x,t)=\rho A\sin(\omega t+kx+b)$

kie b estas la faza ŝovo, kiu enkalkulas la fazon de la kompleksa Γ kaj ankaŭ situon de la punkto de reflektado. Tamen ĉiam eblas tiel elekti la fonton de koordinatosistemo laŭ tempa kaj spaca koordinatoj, ke estu b=0, tiel por simpleco de formuloj estu

$V_{r}(x,t)=\rho A\sin(\omega t+kx)$

La tuteca elektra tensio V_t en la tradona linio estas donita per la kompona principo de ondoj, kiu estas ke la tuteca elektra tensio estas sumo da tensioj de la du ondoj:

$V_{t}(x,t)=A\sin(\omega t-kx)+\rho A\sin(\omega t+kx)$

Per trigonometriaj identoj, ĉi tio povas esti konvertita al la formo:

$V_{t}(x,t)=A{\sqrt {4\rho (\cos(kx))^{2}+(1-\rho )^{2}}}\cos(\omega t+\phi )$

kie $\tan(\phi )={\frac {1+\rho }{1-\rho }}\cot(kx)$

Tiel la amplitudo de elektra tensio je distanco x de la sendilo estas la perioda funkcio

$V_{mot}(x)=A{\sqrt {4\rho (\cos(kx))^{2}+(1-\rho )^{2}}}$

Ĉi tiu varias kun x de minimumo A(1-ρ) al maksimumo A(1+ρ).

Praktikaj implikacioj de staranta onda rilatumo

La plej komuna okazo por mezurado kaj kontrolado de staranta onda rilatumo estas dum instalado kaj agordado de elsendaj antenoj. La sendilo estas konektita al la anteno per nutra linio, la impedanco de la anteno kaj de la nutra linio devas kongrui akurate por maksimuma energia tradono de la nutra linio al la anteno. La impedanco de la anteno varias pro multaj faktoroj, inter kiuj estas: la antena natura resonanco je certaj frekvencoj, la antena alto pli supre de la surfaco de tero, la amplekso de la konduktiloj uzataj por konstrui la antenon.

Se anteno kaj nutrolinio havas ne tute kongruajn impedancoj, iu parto de la elektra energio ne povas esti prenita el la nutrolinio al la anteno. Energio ne tradonita al la anteno estas reflektata reen al la sendilo. La reflektita povumo havas tri ĉefajn implikaciojn en radiaj sendiloj:

• perdo de energio en nutra linio;
• malformigo de signalo en sendilo;
• perdo de energio en sendilo kun ebla damaĝo de la sendilo.

Perdo de energio pligrandiĝas se la staranta onda rilatumo pligrandiĝas.

Kongruigo de la impedanco de la anteno al la impedanco de la nutra linio estas tipe farata per antena agordilo. La agordilo povas esti instalita inter la sendilo kaj la nutra linio, aŭ inter la nutra linio kaj la anteno. Ambaŭ instalaj manieroj permesas al la sendilo operacii je malgranda staranta onda rilatumo, tamen se la agordilo estas instalita je la sendilo, la nutra linio inter la agordisto kaj la anteno operacias kun granda staranta onda rilatumo, kaŭzante aldonan perdon de energio en la nutra linio.

Vidu ankaŭ

• Mezurilo de staranta onda rilatumo
• Elektra impedanco

Eksteraj ligiloj

• Surlinia konvertilo de staranta onda rilatumo
• Teknika informa servo de ARRL pri tradonaj linioj kaj staranta onda rilatumo
• Surlinia kalkulilo de staranta onda rilatumo
• Reflekto kaj tensia staranta onda rilatumo Arkivigite je 2015-06-17 per la retarkivo Wayback Machine
• Komprenado de la fundamentaj principoj de vektora reta analizo Arkivigite je 2010-11-23 per la retarkivo Wayback Machine, Aplika noto 1287-1 de Hewlett Packard, 1997
• Ford, Steve (Aprilo 1997). The SWR Obsession - La obsedo de staranta onda rilatumo (Newington, CT). QST 78 (4) 70–72. ARRL - The national association for Amateur Radio - ARRL - La nacia asocio por Amatora Radio. Kontrolita en 2008-09-26.