Ortangula ondo

Ortangula ondo estas baza speco de ne-sinusa ondformo uzata en elektroniko kaj signal-prilaborado. Ideala ortangula ondo alternas regule inter du niveloj kun malfinie rapidaj trairoj. Unu el la niveloj povas esti nulo, aŭ ĉi tio povas ne esti.
Fontoj kaj uzoj[redakti | redakti fonton]
Ortangulaj ondoj estas ofte aperataj en ciferecaj reŝaltantaj cirkvitoj kaj estas nature generataj per duumaj (du-nivelaj) logikaj aparatoj. Ili estas uzataj kiel tempaj referencoj aŭ taktoj, ĉar ilia rapidaj trairoj taŭgas por funkciigo de sinkronaj logikaj cirkvitoj je precize difinitaj intervaloj. Tamen, kiel la frekvenco-domajna grafikaĵo montras, ortangulaj ondoj enhavas larĝan limigon de harmonikoj; ĉi tiuj povas generi elektromagnetan radiadon aŭ pulsojn de kurento kiu perturbas aliajn apudajn cirkvitojn, kaŭzante bruon aŭ erarojn. Por eviti ĉi tiun problemon en tre delikataj cirkvitoj kiel precizecaj ciferecigiloj, sinusaj ondoj estas uzataj anstataŭ ortangulaj ondoj kiel tempaj referencoj.
En melodia terminoj, ili estas ofte priskribita kiel sonanta kaldrono, kaj estas pro tio uzataj kiel la bazo por blovinstrumentaj sonoj kreataj uzante subtrahan sintezon.
Ekzamenado de la ortangula ondo[redakti | redakti fonton]
La rilatumo de la tempodaŭro de la alta nivelo de la ondo al la tuteca periodo de ortangula ondo estas nomata kiel la deva ciklo. La plej simetria ortangula ondo havas 50% devan ciklon - egalajn altan kaj malaltan tempodaŭrojn. Ankaŭ, la averaĝa nivelo de ortangula ondo estas dependa per la deva ciklo, tiel per variado de la tempodaŭro de la alta nivelo kaj averaĝigo, eblas prezenti ĉiun valoron inter la du niveloj. Ĉi tio estas la bazo de pulsa larĝa modulado.
La ortangula ondo kun 50% deva ciklo enhavas nur neparajn entjerajn harmonikojn. Per serio de Fourier eblas priskribi idealan ortangulan ondon kun 50% deva ciklo kiel malfinia serio de la formo
Specialaĵo de la konverĝo de la prezento per serio de Fourier de la ortangula ondo estas la gibbsa fenomeno. Sonorantaj aĵoj en ne-idealaj ortangulaj ondoj povas esti montritaj al esti rilatanta al ĉi tiu fenomeno. La gibbsa fenomeno povas esti malebligita per la uzo de σ-proksimuma kalkulado, kiu uzas la σ-faktorojn de Lanczos por ke la vico konverĝu pli glate.
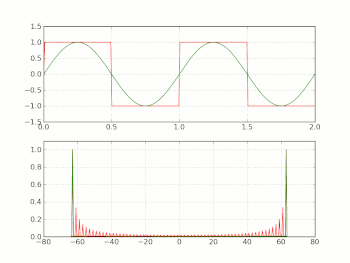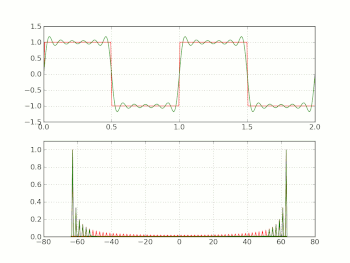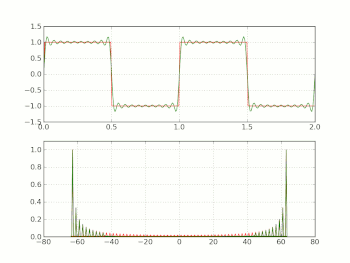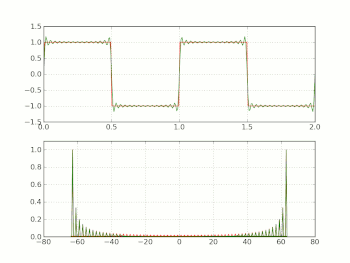
Ideala ortangula ondo postulas ke la signalo ŝanĝiĝu de la alta al la malalta stato kaj reen pure kaj momente. Ĉi tio estas neebla en realo-mondaj sistemoj, ĉar ĝi devus postuli malfinian bendlarĝon.
Realo-mondaj ortangulaj-ondoj havas nur finia bendlarĝon, kaj ofte eksponi sonorantajn efikojn similan al tiuj de la gibbsa fenomeno, aŭ ondetaj efikojn similajn al tiuj de la σ-proksimuma kalkulado.
Por modera proksimuma kalkulado al la ortangulo-onda formo, almenaŭ la fundamenta kaj tria harmonikoj necesas al ĉeesti, kun la kvina harmoniko estanta dezirinda. Ĉi tiuj bendlarĝaj postuloj estas gravaj en cifereca elektroniko, kie finie bendlarĝaj analogaj proksimumigoj al ortangulaj ondoj estas uzataj. La sonorantaj trairoj estas de grava elektronika konsidero ĉi tie, ĉar ili povas transiri la elektrajn limigojn de la cirkvito.
Karakterizaĵoj de neperfektaj ortangulaj ondoj[redakti | redakti fonton]
Kiel ni havi jam menciis, ideala ortangula ondo havas momentajn trairojn inter la alta kaj malaltaj niveloj. En praktiko, ĉi tio estas neniam atingita pro fizikaj limigoj de la sistemo kiu generas la ondformon. La tempodaŭroj prenita por ke la signalo pligrandiĝu de la malalta nivelo al la alta nivelo kaj reen denove estas nomataj kiel la pligrandiĝa tempo kaj la fala tempo respektive.
Se la sistemo estas troamortizita, do la ondformo povas neniam reale atingi la teoriajn altan kaj malaltan nivelojn, kaj se la sistemo estas maltroamortizita, ĝi oscilos ĉirkaŭ la alta kaj malaltaj niveloj antaŭ kvitiĝanta suben. En ĉi tiuj okazoj, la pligrandiĝa kaj fala tempodaŭroj estas mezurataj inter precizigitaj interaj niveloj, kiel 5% kaj 95%, aŭ 10% kaj 90% de la interaĵo. Formuloj ekzistas per kiuj oni povas kalkuli la proksimuman bendlarĝon de sistemo por donitaj la pligrandiĝa kaj fala tempodaŭroj de la ondformo.
Difinoj[redakti | redakti fonton]
La ortangula ondo havas multajn difinojn, kiu estas ekvivalento escepti de la punktoj de malkontinueco, kiuj estas nur du punktoj en ĉiu periodo.
Ĝi povas esti difinita kiel simple la signa funkcio de sinusa funkcio:
- x(t) = sgn(sin(t))
kiu estos esti 1 kiam la sinusa funkcio estas pozitiva, -1 kiam la sinusa funkcio estas negativa, kaj 0 je la malkontinuaĵoj. Ĝi povas ankaŭ esti difinita kun respekto al la hevisida ŝtupara funkcio u(t) aŭ la rektangula funkcio ⊓(t):
T estas 2 por 50% deva ciklo. Ĝi povas ankaŭ esti difinita en popeca maniero:
kaj
- x(t+T) = x(t)



