RLC-cirkvito
En elektra inĝenierarto, RLC-cirkvito estas lineara cirkvito konsistanta el rezistilo, induktilo kaj kondensilo, kiuj estas serie aŭ paralele konektitaj. La parto RLC de la termino originas de la simboloj R de rezistanco, L de induktanco kaj C de kapacitanco. Tiu cirkvito formas harmonan oscililon por elektra kurento, kaj ĝi resonancas. Kontraste kun LC-cirkvito, en kiu oscilado povas daŭri infinite, la rezistilo de RLC-cirkvito amortizas la oscilojn de elektraj vibroj dum finia tempo. Fakte, oni ne povas eviti rezistancojn en realaj cirkvitoj, eĉ se rezistilo ne estas volonte inkluzivita. Pura LC-cirkvito ekzistas nur teorie, same pura induktilo (L) aŭ kondensilo (C) ne ekzistas sen rezistanco.
Seria RLC-cirkvito[redakti | redakti fonton]
La diferenciala ekvacio kiu regas la serian cirkviton estas la sekvanta:
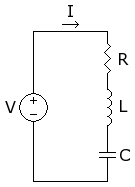 |
| Figure 1. Seria RLC-cirkvito. |
|
aliskribante:
kie :
- estas la kurentintenso, kiu trafluas la montaĵon (A) ;
- estas la tensio inter la bornoj de la generatoro (V) ;
- estas la tuta rezistanco (inkluzive tiujn de la konduktiloj) de la cirkvito (Ω) ;
- estas la induktanco de la bobeno (H) ;
- estas la kapacitanco de la kondensatoro (F) ;
- estas la tempo (s) ;
- estas enda variablo por la integralo (s).
-Pri kontinua fonto, , konstanta valoro, do:
tial sekvas ke
Post longa tempo, , kaj la kurento ĉesas
ĉar la tensio de la kondensilo atingis la valoron de la fonto.
-Pri nedaŭra solvo, oni konsideras homogenan ekvacio kun .
Difinante kaj en sama unuo de angula frekvenco, oni povas skribi:
kie estas la "konstanto de amortizo", kiu permesas mezuri la progresan malpliiĝon laŭ tempo de la kurento, malantaŭ la malapero de altruda fonto, kaj estas la propra angula frekvenco de resonanco, laŭ sekvanta priskribo.
Pri seriaj RLC-cirkvitoj:
Utila parametro estas la "rilatumo de amortizo" , kiu difiniĝas per la kvociento de tiuj du parametroj:
Tiu valoro de la "rilatumo de amortizo" determinas la tipon de nedaŭra kurento (aŭ de pasema tensio) tra la cirkvito.
La solvo de la ordinara diferenciala ekvacio malsamas laŭ la valoroj de : (granda amortizo), (kriza amortizo, t.e. la minimuma lima amortizo, kiu tamen evitas osciladon), aŭ (malgranda amortizo).
La ĝenerala solvaĵo de la ODE estas sumo de nedaŭra solvo de la homogena ODE (kie dependas de komencoj kondicoj), kaj de la daŭra solvo (kiu dependas de la dua termo en la nehomogena ODE).
Oni povas skribi la solvaĵon per sumo de eksponentaj funkcioj kun reelaj () aŭ imaginaraj () eksponentoj.
La koeficientoj A1 kaj A2 estas determinataj per la komencaj kurentoj kaj tensioj, kaj iliaj supozataj valoroj post infinita tempo.
Pri granda amortizo ():
tio estas kadukiĝo de la nedaŭra kurento sen oscilado.
Pri kriza amortizo ():
tio korespondas al kiel eble plej rapida malkresko de signalo sen oscilo, kaj sen superpasi la stabilan valoron. Tiu propreco estas grava en regado de procezoj, pri kiuj necesas atingi dezideritan staton kiel eble plej rapide sen supertensio. osenestas kadukiĝo de la nedaŭra kurento sen oscilado. D1 kaj D2 estas konstantoj determinataj per komencaj kondiĉoj.
Pri malgranda amortizo ():
tio estas malgrandiĝo de la nedaŭra kurento per , laŭ frekvenco donata per:
Aplikante la trigonometriaj identoj, la du trigonometriaj funkcioj povas esti anstataŭataj per unu sinusa funkcio kun aldonata fazo:
La eksponento ( priskribas la eksponentan malkreskon de la amplitudoj. B1 kaj B2 (aŭ B3, kaj la fazo de delokiĝo, laŭ la dua formo de la formulado) estas determinataj per komencaj kondiĉoj.
estas la angula frekvenco de resonanco en la amortizita cirkvito, aŭ ankoraŭ la frekvenco de la cirkvito laŭ ĝi nature oscilas, sen gvidanta ekstera fonto;
estas la angula frekvenco laŭ kiu la cirkvito resonancas, kiam gvidata per ekstera fonto; ĝi estas ankaŭ la propra angula frekvenco de resonanco sen amortizo, t.e. kiam .

-Pri alterna fonto, , oni konsideras kompleksan impedancon por kalkuli la kurenton:
kie:
kies absoluta valoro estas
La amplitudo de la kurento do estas:
Kiam la angula frekvenco de la generatoro estas
ĝi korespondas al la frekvenco de resonanco
tiel la oscilcirkvito montras nur oman rezistancon:
la kurento maksimumas:
Plie la tensioj de la kondensilo kaj de la induktilo oponas:
ĉar estas interŝanĝo de elektra energio inter induktilo kaj kondensilo.
Oni difinas la koeficienton de supertensio Q (Q-faktoro), kiu estas la kvociento inter la tensio de la induktilo (aŭ de la kondensilo) kaj la tensio de la fonto (aŭ de la rezistilo):
Ju pli la rezistanco R estas malgranda (malgranda oma perdado), des pli la koeficiento de supertensio estas granda.
Paralela RLC-cirkvito[redakti | redakti fonton]
Dum la tensioj de la elementoj de seria cirkvito adicias, estas la kurentoj de la elementoj de paralela cirkvito kiuj adicias.
Pro la kondensilo, oni ne povas apliki rekte kontinuan tension sen pero de protekta rezistilo inter la fonto kaj la paralela cirkvito. Taŭgas pli bone uzi kurento-fonton kiel generatoron.
La diferenciala ekvacio (ODE), kiu regas la paralelan cirkviton estas la sekvanta:
aliskribante:
kie :
- estas la kurentintenso, kiu trafluas la montaĵon (A) ;
- estas la tensio inter la bornoj de la generatoro (V) ;
- estas la tuta paralela rezistanco (inkluzive tiujn de la konduktiloj) de la cirkvito (Ω) ;
- estas la induktanco de la bobeno (H) ;
- estas la kapacitanco de la kondensatoro (F) ;
- estas la tempo (s) ;
- estas enda variablo por la integralo (s).
Pri fonto de kontinua kurento, , konstanta valoro, do:
tial sekvas ke
Fare de la induktilo, pro la kurento-fonto, la tensio de la montaĵo nuliĝas post longa tempo, ĉar tiam .
Por eviti tion, la generatoro devas ŝanĝi sian signon, ekzemple per livero de triangula alterna kurento.
Same kiel la seria cirkvito, oni povas difini la konstanton de amortizo :
- kaj la rilatumon de amortizo :
Pri la nedaŭra analizo, la komencaj kondiĉoj estas:
- , la kurento de la induktilo konservas sian antaŭan valoron.
- , la tensio de la kondenatoro konservas sian antaŭan valoron.
Pri fonto de alterna kurento
kie
estas la kompleksa admitanco (inverso de la impedanco) de tiu montaĵo.
Kiam la angula frekvenco de la generatoro estas
ĝi korespondas al la frekvenco de resonanco
tiel la oscilcirkvito montras nur oman rezistancon:
plie la tensioj de la kondensilo kaj de la induktilo oponas:
ĉar estas interŝanĝo de elektra energio inter induktilo kaj kondensilo.
Same kiel la seria cirkvito, oni difinas la koeficienton de supertensio Q ( aŭ Q-faktoro) (sed laŭ tiu aparta kazo taŭgus pli bone la termino "koeficento de superkurento"), kiu estas la kvociento inter la kurento de la induktilo (aŭ de la kondensilo) kaj la kurento de la fonto (aŭ de la rezistilo):
Ju pli la rezistanco R estas granda (malgranda oma perdado), des pli la koeficiento de supertensio estas granda.
Aplikoj de RLC-cirkvitoj[redakti | redakti fonton]
La RLC-cirkvitoj estas ĝenerale uzitaj por konstrui telekomunikadajn filtrilojn de frekvenco (ekz. en radioaparatoj). Tiuj cirkvitoj povas enhavi plurajn induktilojn kaj plurajn kondensilojn: oni nomas ilin LC-retoj.
Vidu ankaŭ[redakti | redakti fonton]
Eksteraj ligiloj[redakti | redakti fonton]
- Java-Applet[rompita ligilo] Vidigo de oscilado laŭ rezistanco, induktanco kaj kapacitanco (germane)
- Resonanco de cirkvito RLC de Hyperphysics (angle)
































































