Racionala trigonometrio

Matematiko > Trigonometrio > Racionala trigonometrio

Racionala trigonometrio estas moderna ideo pri trigonometrio implikanta etendeco kaj kvadranco anstataŭ angulo kaj distanco. Ĉi tiu nova maniero estas la laboro de Doktoro Norman Wildberger de la Universitato de Nova Sud-Kimrio (ĉe Sidnejo en Aŭstralio). Pli da informo estas havebla je lia paĝaro [1]. Anstataŭ la klasikaj funkcioj (sinuso, kosinuso, tangento) ĝi uzas nur algebrajn operaciojn.

Ĝia nomo devenas de la malplia uzado de neracionalaj nombroj, kiel kvadratoradikoj kaj la matematika konstanto π kiu estas neracionala.

Fundamentaj Kvantoj - kvadranco kaj etendeco

Kiel matematiko adoptis la araban ciferan sistemon kun nulo kaj lok-valoro anstataŭ romanaj numeraloj, simile trigonometrio bonfarus adopti ĉi tiujn ideojn de Doktoro Wildberger. Eble la individuaj partoj ne estas novaj, sed la sugeston ke ili povas kombini por krei novan trigonometrion meritas rimarkon. Antaŭ la tempo de Koperniko, astronomoj referencis tabelojn por kalkuli la kontraŭmovadon de la planedoj, kion ili ne povis ekspliki. Sammaniere, modernaj lernantoj ĉe mezlernejoj ĉien referencas tabelojn aŭ kalkulilojn por trovi trigonometriajn proporciojn. Wildberger redifinas trigonometrion el novajn kvantojn kaj uzas la koordinatan sistemon rekte por solvi geometriajn problemojn.

Kvadranco - la apartiĝo inter punktoj

Kvadranco ("$Q$") diferencas ol simpla distanco ĉar ĝi kvadratigas la distancon. Ĉi tio signifas ke oni povas plifacile kalkuli la apartiĝo inter du punktoj en 2-dimensia spaco ĉar si ne devas trovi la kvadratoradikon, kiu ofte estas neracionala.

En kartezia spaco $(x,y)$, inter la punktoj $p_{1}$ kaj $p_{2}$, la kvadranco $Q_{\mathrm {1-2} }$ estas difinita kiel,

$Q_{\mathrm {1-2} }=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Etendeco - la apartiĝo inter linioj

Laŭ racionala trigonometrio, etendeco ("$s$") estas fundamenta koncepto difinita kiel la proporcio de du kvadrancoj. Establu punkto $p_{1}$ kie du linioj kruciĝas, kaj elektu du punktojn $p_{2}$ sur unu kaj $p_{3}$ sur la alia tiel, kiel la linio $\ell _{\mathrm {2-3} }$ estas orta laŭ $\ell _{\mathrm {1-3} }$.

Inter la linioj $\ell _{\mathrm {1-2} }$ kaj $\ell _{\mathrm {1-3} }$, la etendeco $s_{1}$ estas difinita kiel,

$s_{1}={Q_{\mathrm {1-3} } \over Q_{\mathrm {1-2} }}$

Komparita kun la Tradiciaj Geometriaj Konceptoj

Kvadranco komparita kun distanco:

$Q=(\mathrm {distanco} )^{2}$

Etendeco komparita kun angulo (dum angulo estas akuta):

$s=(\sin(\mathrm {angulo} ))^{2}$

Etendeco ne estas sama kiel la koncepto en tradicia geometrio de angulo. Etendeco priskribas rilato inter du linioj, de paraleleco ĝis orteco, sed angulo priskribas rilato inter du radioj emanantaj el la sama punkto. Plue, ĉar etendeco kaj angulo 'ne' estas linie proporciaj, oni ne povas adicii etendecoj tiom simple kiel anguloj.

Leĝoj de Racionala Trigonometrio

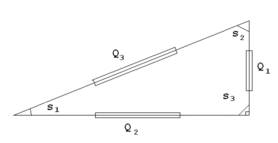
La Tri-Kvadranca Formulo

Kiam tri punktoj kuŝas estas samliniaj (restantaj en sama linio), la sekvanta esprimo estas vera:

$(Q_{1}+Q_{2}+Q_{3})^{2}=2(Q_{1}^{2}+Q_{2}^{2}+Q_{3}^{2})$

La Pitagora Teorio

La facetoj $\ell _{1}$ kaj $\ell _{2}$ de triangulo kruciĝas orte kiam,

$Q_{1}+Q_{2}=Q_{3}$

La Etendeca Leĝo

Je ia triangulo kun ne-nulaj kvadrancoj,

${s_{1} \over Q_{1}}={s_{2} \over Q_{2}}={s_{3} \over Q_{3}}$

La Kruca Leĝo

Je ia triangulo, difinu la krucon, $c_{3}=1-s_{3}$. Tiel,

$(Q_{1}+Q_{2}-Q_{3})^{2}=4Q_{1}Q_{2}c_{3}$

La Tri-Etendeca Formulo

Je ia triangulo,

$(s_{1}+s_{2}+s_{3})^{2}=2(s_{1}^{2}+s_{2}^{2}+s_{3}^{2})+4s_{1}s_{2}s_{3}$

Por Speguligi Etendecojn

Etendecojn ne adicias linie kiel anguloj. Anstataŭe, oni povas trovi la etendecon enhavantan ambaŭ flankojn de speguligita etendeco (same kiel duobligita angulo). Do la etendeco de linio al ĝia speguligitaĵo estas,

$s_{\mathrm {speguligita} }=4s(1-s)$

Eksteraj ligiloj

• Divine Proportions (angle) - la libro de Norman Wildberger.