Izolita punkto
| Por aliaj signifoj, bv. rigardi la apartigilan paĝon: Izolita punkto (kurbo) |
En topologio, punkto x de aro S estas nomita kiel izolita punkto, se tie ekzistas najbareco de x ne enhavanta aliajn punktojn de S.
Aparte, en eŭklida spaco (aŭ en metrika spaco), x estas izolita punkto de S, se oni povas trovi malfermitan pilko ĉirkaŭ x kiu ne enhavas aliajn punktojn de S.
Ekvivalente, punkto x estas ne izolita se kaj nur se x estas limiga punkto.
Aro kiu estas farita nur de izolitaj punktoj estas nomita kiel diskreta aro . Diskreta subaro de eŭklida spaco estas kalkulebla; tamen, aro povas esti kalkulebla sed ne diskreta, ekzemple racionalaj nombroj.
Fermita aro sen izolitaj punktoj estas nomita kiel perfekta aro.
Ekzemploj[redakti | redakti fonton]
Topologiaj spacoj en jenaj ekzemploj estas konsideritaj kiel subspacoj de la reela linio.
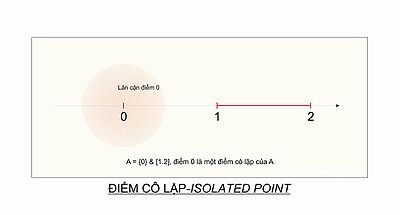
- Por aro , la punkto 0 estas izolita punkto.
- Por aro , ĉiu punktoj 1/k estas izolitaj punktoj, sed 0 estas ne izolita punkto ĉar estas aliaj punktoj en S tiel proksime al 0 kiel oni deziras.
- Aro N={0, 1, 2, ...} de naturaj nombroj estas diskreta aro.

![{\displaystyle S=\{0\}\cup [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91214dd46eb1ba30f1b8ad577c4820f6985242e6)
