Apartiga aksiomo
En topologio kaj rilatantaj kampoj de matematiko, estas kelkaj limigoj kiujn oni ofte konstruas sur la specoj de topologiaj spacaj kiujn onu deziras konsideri. Iu el ĉi tiuj limigoj estas donita per la apartigaj aksiomoj. Ili estas iam nomitaj kiel apartigaj aksiomoj de Tiĥonov, honore al Andrej Tiĥonov.
La apartigaj aksiomoj estas aksiomoj nur en la senco, ke difinante la nocion de topologia spaco, oni povus aldoni ĉi tiujn kondiĉojn kiel superfluaj aksiomoj por preni pli limigitan nocion de tio, kia estas topologia spaco. La moderna aliro estas fiksi verecon aŭ ne postulon de vereco de apartigaj aksiomoj por ĉiu aksiomigo de topologia spaco kaj tiam paroli pri specoj de topologiaj spacoj. Tamen, la termino "apartiga aksiomo" enradikiĝis. La apartigaj aksiomoj estas signitaj per la litero) "T" post la Germana "Trennung", signifas apartigo.
La precizaj signifoj de la terminoj asociitaj kun la apartigaj aksiomoj diversiĝis tra la tempo, kiel estas eksplikite en historio de la apartigaj aksiomoj. Aparte legante pli malnovan literaturon, necesas certiĝi en kompreno de uzataj de la aŭtoro difinoj de ĉiu kondiĉoj.
Antaŭ oni difinas la spacoj priskribitajn per la apartigaj aksiomoj, oni bezonas difini iun terminologion por doni konkretan signifon al la koncepto de apartigo.
Apartigitaj aroj kaj topologie distingeblaj punktoj
[redakti | redakti fonton]La apartigaj aksiomoj koncernas la uzon de topologiaj signifoj por distingi disajn arojn kaj malsamaj punktojn. Ne sufiĉas por eroj de topologia spaco esti malsamaj; oni povas bezoni ke ili estu topologie distingeblaj. Simile ne sufiĉas por subaroj de topologia spaco esti disaj; oni povas bezoni ke ili estu apartigitaj (en iu ajn el diversaj manieroj).
La apartigaj aksiomoj ĉiuj diras, en unu aŭ alia direkto, ke punktoj aŭ aroj, kiuj estas distingeblaj aŭ apartigitaj en iu malforta senco devas ankaŭ esti apartigitaj en iu pli forta senco.
Lasu ke X estu topologia spaco. Tiam du subaroj A kaj B de X estas apartigitaj se ĉiu el ili estas disa de la fermaĵo de la alia. Iuj ajn du apartigitaj aroj devas esti disaj.
Estas kelkaj pli fortaj formoj de aparteco por aroj; ili estas laŭorde: apartigita per najbaraĵoj; apartigita per fermitaj najbaraĵoj, apartigita per funkcio, kaj apartigita precize per funkcio. Ĉi tiuj estas difinitaj kaj diskutitaj en la artikolaj apartigitaj aroj.
Apartigitaj aroj estas malsamaj de apartigitaj spacoj, difinitaj pli sube.
Oni iam uzi la terminologion de apartigitaj aroj por nomi la punktojn; en tiu situacio, reale temas pri la unuera aro {x} sed ne la punkto x. Se A kaj B estas malfermitaj kaj disaj, tiam ili devas esti apartigitaj per najbaraĵoj; nur prenu ke U := A kaj V := B. Por tiu kaŭzo, multaj apartigaj aksiomoj koncernas aparte fermitajn arojn.
Du punktoj x kaj y en X estas topologie distingebla se kaj nur se ili ne havas ĝuste la samajn najbaraĵojn. Se du punktoj estas topologie distingeblaj, tiam certe ili estas malsamaj. Plue, se la x kaj y estas apartigitaj (ĉi tio estas se la unueraj aroj {x} kaj {y} estas apartigitaj), tiam ili estas ankaŭ topologie distingeblaj.
Por pli pri topologie distingeblaj punktoj, vidu en topologian distingebleco.
Difinoj de la aksiomoj
[redakti | redakti fonton]Multaj el ĉi tiuj nomoj havas alternativajn signifojn en iom el la matematika literaturo, kiel eksplikis sur Historio de la apartigaj aksiomoj; ekzemple, la signifoj de "normala" kaj "T4" estas iam interŝanĝitaj, simile "regula" kaj "T3", kaj tiel plu. Multaj el la konceptoj ankaŭ havas kelkajn nomojn.
La plejparto el ĉi tiuj aksiomoj havas alternativajn difinojn kun la sama signifo; la difinoj donita jen tiuj kiu falas en konsekvencan ŝablonon rilatante al diversaj (komprenaĵoj, nocioj) de apartigo difinitaj en la antaŭa sekcio. Aliaj eblaj difinoj povas troviĝi en la personaj artikoloj.
Totale de jenaj difinoj, X estas denove topologia spaco, kaj ĉiuj funkcioj estas supozitaj esti kontinuaj.
X estas T0 aŭ spaco de Kolmogorov se iuj ajn du malsamaj punktoj en X estas topologie distingebla. Estos esti komuna temo inter la apartigaj aksiomoj havi unu version de aksiomo, kiu postulas T0 kaj unu version, kiu ne.
X estas R0 aŭ simetria se iuj ajn du topologie distingeblaj punktoj en X havas disajn fermaĵojn.
X estas T1 aŭ alirebla aŭ spaco de Fréchet se iuj ajn du malsamaj punktoj en X havas disajn fermaĵojn. Tial, X estas T1 se kaj nur se ĝi estas kaj T0 kaj R0. Kvankam estas uzataj terminoj kiel "T1 spaco", "topologio de Fréchet", kaj "topologia spaco X estas de Fréchet", eviteblas uzi terminon "spaco de Fréchet" en ĉi tiu ĉirkaŭteksto, ĉar estas la alia tute malsama nocio de freŝea spaco en funkcionala analitiko.
X estas R1 aŭ antaŭregula se iuj ajn du topologie distingeblaj punktoj en X estas apartigitaj per najbaraĵoj. R1 spaco devas ankaŭ esti R0.
X estas T2 aŭ spaco de Hausdorff (hausdorff-a) aŭ apartigita se iuj ajn du malsamaj punktoj en X estas apartigitaj per najbaraĵoj. Tial, X estas Hausdorff-a se kaj nur se ĝi estas kaj T0 kaj R1. Hausdorff-a spaco devas ankaŭ esti T1.
X estas T2½ aŭ urysohn-a se iuj ajn du malsamaj punktoj en X estas apartigitaj per fermitaj najbaraĵoj. T2½ spaco devas ankaŭ esti hausdorff-a.
X estas plene hausdorff-a aŭ plene T2 se iuj ajn du malsamaj punktoj en X estas apartigitaj per funkcio. Plene hausdorff-a spaco devas ankaŭ esti T2½.
X estas regula se iuj ajn donitaj punkto x kaj fermita aro F en X, se x ne apartenas al F, tiam x kaj F estas apartigitaj per najbaraĵoj. Fakte, en regula spaco, iuj ajn tia x kaj F ankaŭ estas apartigitaj per fermitaj najbaraĵoj. Regula spaco devas ankaŭ esti R1.
X estas T3 aŭ regula hausdorff-a se ĝi estas kaj T0 kaj regula. Regula hausdorff-a spaco devas ankaŭ esti T2½.
X estas plene regula se iuj ajn donitaj punkto x kaj fermita aro F en X, se x ne apartenas al F, tiam x kaj F estas apartigitaj per funkcio. Plene regula spaco devas ankaŭ esti regula.
X estas T3½ aŭ plene T3 aŭ tychonoff-a aŭ plene regula hausdorff-a se ĝi estas ambaŭ T0 kaj plene regula. Spaco de Tychonoff devas ankaŭ esti ambaŭ regula Hausdorff-a kaj plene Hausdorff-a.
X estas normala se iuj ajn du disaj fermitaj subaroj de X estas apartigitaj per najbaraĵoj. Fakte, en normala spaco, iuj ajn du disaj fermitaj aroj ankaŭ estas apartigitaj per funkcio; ĉi tiu estas lemo de Urysohn.
X estas T4 aŭ normala hausdorff-a se ĝi estas T1 kaj normala. Normala hausdorff-a spaco devas ankaŭ esti kaj tychonoff-a kaj normala regula.
X estas plene normala se iuj ajn du apartigitaj aroj estas apartigitaj per najbaraĵoj. Plene normala spaco devas ankaŭ esti normala.
X estas T5 aŭ plene T4 aŭ plene normala hausdorff-a se ĝi estas ambaŭ plene normala kaj T1. T5 spaco devas ankaŭ esti T4.
X estas perfekte normala se iuj ajn du disaj fermitaj aroj estas precize apartigitaj per funkcio. Perfekte normala spaco devas ankaŭ esti plene normala.
X estas T6 aŭ perfekte normala hausdorff-a aŭ perfekte T4, se ĝi estas kaj perfekte normala kaj T1. Perfekte T4 spaco devas ankaŭ esti T5.
Interrilatoj inter la aksiomoj
[redakti | redakti fonton]La aksiomo T0 estas speciala en tio, ke ĝi povas esti ne nur aldonita al propraĵo (tiel ke regula plus T0 estas T3) sed ankaŭ subtrahita de propraĵo (tiel ke Hausdorff-a minus T0 estas antaŭregula), en honeste preciza senco; vidu plu en kvociento de Kolmogorov. Kiam aplikita al la apartigaj aksiomoj, ĉi tio kondukas al la interrilatoj donitaj en la tabelo pli sube:
| T0 versio | Ne T0 versio |
|---|---|
| T0 | Ne estas postulata |
| T1 | R0 |
| Hausdorff-a | Antaŭregula (R1) |
| T2½ | (Sen speciala nomo) |
| Plene hausdorff-a | (Sen speciala nomo) |
| Regula hausdorff-a (T3) | Regula |
| Tychonoff-a (T3½) | Plene regula |
| Normala T0 | Normala |
| Normala Hausdorff-a (T4) | Normala regula |
| Plene normala T0 | Plene normala |
| Plene normala hausdorff-a (T5) | Plene normala regula |
| Perfekte normala T0 | Perfekte normala |
| Perfekte normala hausdorff-a | Perfekte normala regula |
En ĉi tiu tabelo iro de dekstra kolumno al maldekstra kolumno estas per aldono de la bezono de T0, kaj iro de maldekstra kolumno al dekstra kolumno estas per forprenado de la bezono de T0 uzante la kvocientan operacion de Kolmogorov.
Escepte la inkluziveco aŭ neinkluziveco de T0, la interrilatoj inter la apartigaj aksiomoj estas indikitaj en jena figuro:
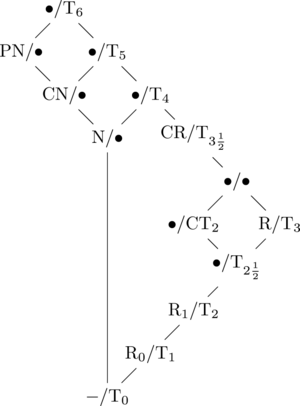
En ĉi tiu figuro, la ne T0 versio de kondiĉo estas en maldekstra flanko de la oblikvo, kaj la T0 versio estas en dekstra flanko. Literoj estas uzataj por mallongigo kiel sekvas: "P" = "perfekte", "C" = "plena", "N" = "normala", kaj "R" (sen suba indico) = "regula". Kuglo indikas, ke ne estas speciala nomo por spaco de tiu speco. La haltostreko je la fundo indikas ne kondiĉo.
Oni povas kombini du propraĵojn uzante tiun figuron sekvante la figuron supren ĝis ambaŭ kiam branĉoj kuniĝas. Ekzemple, se spaco estas kaj plene normala ("CN") kaj plene hausdorff-a ("CT2"), tiam sekvante ambaŭ branĉojn supren, oni trovos la eron "•/T5". Ĉar plene hausdorff-aj spacoj estas T0 (eĉ kvankam plene normalaj spacoj povas ne esti T0), ini prenas la T0 flankon de la oblikvo, do, plene normala plene hausdorff-a spaco estas la sama kiel T5 spaco.
Kiel eblas vidi de la figuro, normala kaj R0 kune enhavas aregon de aliaj propraĵoj. Ĉar reguleco estas la plej fame konata propraĵo de ĉi tiuj spacoj, spaco kiu estas kaj normala kaj R0 estas tipe nomata kiel "normala regula spaco". En ia simila maniero, T4 spaco estas ofte nomata kiel "normalaj hausdorff-a spaco" fare de tiuj, kiuj deziras eviti la "T"-notacion (ĉar "T"-notacio estas malpli verŝajne esti unusence komprenita). Ĉi tiuj konvencioj povas esti ĝeneraligitaj al aliaj regulaj kaj hausdorff-aj spacoj.
Aliaj apartigaj aksiomoj
[redakti | redakti fonton]Estas iuj aliaj kondiĉoj sur topologiaj spacoj, kiuj estas iam klasifikitaj kun la apartigaj aksiomoj, sed ĉi tiuj ne konformas kun la kutimaj apartigaj aksiomoj tiel plene.
X estas duonregula se la regulaj malfermitaj aroj formas bazon por la malfermitaj aroj de X. Iu ajn regula spaco devas ankaŭ esti duonregula.
X estas plene normala se ĉiu malfermita kovro estas malfermita stela bonmaniereco. Ĉiu plene normala spaco devas ankaŭ esti kaj normala regula kaj parakompakta. Fakte, plene normalaj spacoj reale pli rilatas al parakompakteco ol al la kutimaj apartigaj aksiomoj.
X estas plene T4, aŭ plene normala hausdorff-a, se ĝi estas kaj T1 kaj plene normala. Plene T4 spaco devas ankaŭ esti T4.
X estas malebria se, por ĉiu fermita aro C kiu estas ne la (eble ne disa) unio de du pli malgrandaj fermitaj aroj, estas unika punkto p tia, ke fermaĵo de {p} egalas al C. Pli lakone, ĉiu nereduktebla fermita aro havas unikan ĝeneralan punkton.
