Duvertica pluredro
| Regula duvertica pluredro | |
| Plia nomo | Aro de regulaj q-lateraj duverticaj pluredroj |
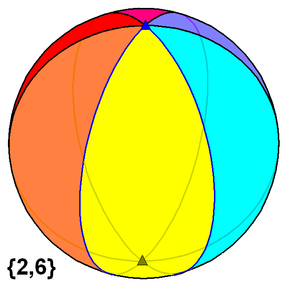 Seslatera duvertica pluredro kiel kahelaro de sfero | |
| Speco | Regula pluredro aŭ sfera kahelaro |
| Vertica figuro | 2q |
| Simbolo de Wythoff | q | 2 2 |
| Simbolo de Schläfli | {2,q} |
| Figuro de Coxeter-Dynkin | |
| Verticoj | 2 |
| Lateroj | q |
| Edroj | q dulateroj |
| Geometria simetria grupo | Duedra simetrio Dqh |
| Duala | Duedro |


En geometrio, n-latera duvertica pluredro estas pluredro, konsistanata el n dulateraj edroj kiu havas la samajn du verticojn.
En eŭklida spaco ĉiuj lateroj koincidas kaj ĝi estas degenera.
Sed ĝi povas esti nedegenera estante konsiderata kiel kahelaro de sfero konsistanta el lunoj sur sfero, tia ke ĉiu luno komunigas la samajn du verticojn.
Regula duvertica pluredro estas tiu kun ĉiuj edroj egalaj. Ĝia simbolo de Schläfli estas {2, n}.
Duverticaj pluredroj kiel regulaj pluredroj
[redakti | redakti fonton]Por regula pluredro kies simbolo de Schläfli estas {m, n}, la kvanto de plurlateraj edroj estas
La platonaj solidoj sciataj ekde antikveco estas la nuraj entjeraj solvaĵoj por m ≥ 3 kaj n ≥ 3. La limigo m ≥ 3 signifas ke la ĉiu plurlatera edro devas havi almenaŭ tri laterojn.
Kiam pluredroj estas konsiderantaj kiel kahelaroj sur sfero, ĉi tiu limigo povas esti malstreĉiĝita, pro tio ke dulateroj povas esti prezentitaj kiel sferaj lunoj, havante ne-nulan areon. Permesante valoron m = 2 oni ricevas la novan malfinian familion de regulaj pluredroj, kiu estas la duverticaj pluredroj. Sur sfero, la pluredro {2, n} estas prezentata kiel n limtuŝantaj lunoj, kun enaj anguloj de 2π/n. Ĉiuj ĉi tiuj lunoj komunigas du komunajn verticojn.
Malstreĉiĝo n = 2 ĉi tie rezultigas duedron.
Derivitaj pluredroj
[redakti | redakti fonton]La duala de la n-latera duvertica pluredro {2, n} estas la n-latera duedro, {n, 2}. La pluredro {2,2} estas mem-duala, kaj estas samtempe duvertica pluredro kaj duedro.
Duvertica pluredro povas esti modifita en la sama maniero kiel la aliaj pluredroj al produkti senpintigita variado. La senpintigita n-latera duvertica pluredro estas n-latera prismo.
Duvertica hiperpluredro
[redakti | redakti fonton]Duvertica hiperpluredro estas hiperpluredro, multdimensia analogo de 3-dimensia duvertica pluredro. Simbolo de Schläfli de duvertica hiperpluredro estas {2,...,2,q}. Duvertica hiperpluredro havas du verticojn.
La du-dimensia duvertica hiperpluredro estas dulatero {2}.
Vidu ankaŭ
[redakti | redakti fonton]Referencoj
[redakti | redakti fonton]- H. S. M. Coxeter, Regular Polytopes - Regulaj hiperpluredroj, 3-a. red., Dover Publications, 1973. ISBN 0-486-61480-8


