Regula pluredro
Regula pluredro estas pluredro kies edroj estas kongruaj (egalaj) regulaj plurlateroj kaj estas muntitaj en la sama maniero ĉirkaŭ ĉiu vertico. Regula pluredro estas alte simetria, latero-transitiva, vertico-transitiva kaj edro-transitiva - kio estas ke ĝi estas transitiva je siaj flagoj. La lasta sola propozicio estas sufiĉa difino.
Regula pluredro estas 3-dimensia regula hiperpluredro. Ĝiaj analogoj estas regula plurlatero en 2 dimensioj kaj regula plurĉelo en 4 dimensioj.
Regula pluredro estas identigita per ĝia simbolo de Schläfli de la formo {n, m}, kie n estas kvanto de lateroj de ĉiu edro kaj m kvanto de edroj kuniĝantaj je ĉiu vertico.
La 9 regulaj pluredroj
[redakti | redakti fonton]Estas 5 konveksaj regulaj pluredroj, nomataj kiel platonaj solidoj:

|
|

|

|

|
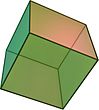
| Kvaredro {3, 3} | Kubo {4, 3} | Okedro {3, 4} | Dekduedro {5, 3} | Dudekedro {3, 5} |
Estas 4 nekonveksaj regulaj pluredroj, nomataj kiel pluredroj de Keplero-Poinsot:

|

|

|

|
| Malgranda steligita dekduedro {5/2, 5} | Granda steligita dekduedro {5/2, 3} | Granda dekduedro {5, 5/2} | Granda dudekedro {3, 5/2} |
Karakterizoj
[redakti | redakti fonton]Ekvivalentaj propraĵoj
[redakti | redakti fonton]La propraĵo de havo de la sama ordigo de edroj ĉirkaŭ ĉiu vertico povas esti anstataŭigita per ĉiu el jenaj ekvivalentaj kondiĉoj en la difino:
- La verticoj de la pluredro ĉiuj kuŝas sur sfero.
- Ĉiuj duedraj anguloj de la pluredro estas egalaj.
- Ĉiuj verticaj figuroj de la pluredro estas regulaj plurlateroj.
- Ĉiuj solidaj anguloj de la pluredro estas kongruaj.
Samcentraj sferoj
[redakti | redakti fonton]Regula pluredro havas ĉiujn de tri rilatantajn sferoj kun komuna centro:
- Enskribita sfero, tangenta al ĉiuj edroj.
- Mezosfero, tangenta al ĉiuj lateroj.
- Ĉirkaŭskribita sfero, trapasanta ĉiujn verticojn.
Je ĉiu alia pluredro mankas almenaŭ unu speco de la sfero.
Simetrio
[redakti | redakti fonton]La regulaj pluredroj estas la plej simetria el ĉiuj pluredroj. Ĉiu el ili apartenas el unu el tri geometriaj simetriaj grupoj, kiuj estas nomita pro ili:
- Kvaredra simetrio - kvaredro
- Okedra simetrio - okedro kaj kubo
- Dekduedra simetrio - ĉiuj la aliaj el la 9
Eŭlera karakterizo
[redakti | redakti fonton]Ĉiu el la 5 konveksaj havas eŭleran karakterizon egalan al 2, ĉar havas randon topologie ekvivalentan al sfero. Iuj el la 4 nekonveksaj havas malsaman valoron, ĉar havas randon topologie ne ekvivalentan al sfero.
Dualeco
[redakti | redakti fonton]La regulaj pluredroj estas en paroj de interdualaj pluredroj
- La kvaredro estas mem duala, do ĝi estas paro kun si.
- La kubo kaj okedro estas duala al unu la alia.
- La dudekedro kaj dekduedro estas duala al unu la alia.
- La malgranda steligita dekduedro kaj granda dekduedro estas duala al unu la alia.
- La granda steligita dekduedro kaj granda dudekedro estas duala al unu la alia.
Regulaj pluredroj en naturo
[redakti | redakti fonton]
Ĉiuj platonaj solidoj okazas en naturo kiel formo de io.
La kvaredro, kubo, kaj okedro ĉiuj okazas kiel kristaloj, kvankam estadas ankaŭ la aliaj formoj de kristaloj. La regula dudekedro kaj regula dekduedro ne estadas kiel formoj de kristaloj, kvankam unu formo de kristalo, piritopluredro, estas neregula dekduedro, ĝi havas dek du kvinlaterajn edrojn same ordigitajn kiel edroj de la regula dekduedro.
Regulaj pluredraj formoj aperas ankaŭ en biologiaj objektoj. Ekzistas specioj de radiolaria, skeletaj sistemoj de kiuj estas formitaj simile al diversaj regulaj pluredroj. Inter ili estas Circoporus octahedrus, Circogonia icosahedra, Circorrhegma dodecahedra, Lithocubus geometricus; la unuaj tri havas formojn similajn al okedro, dudekedro, dekduedro respektive. La eksteraj proteinaj ŝeloj de multaj virusoj havas formojn de regulaj pluredroj. Ekzemple, HIV estas enmetita en regulan dudekedron.
Specoj de karbonaj molekuloj, (fulerenoj) estas formitaj simile al diversaj regulaj pluredroj. C60, la plej facile produktita fulereno, aspektas pli-malpli sfera, ĝia formo estas proksimume senpintigita dudekedro (kiu estas neregula pluredro). Tamen la molekuloj kun pli multaj atomoj, ekzemple C240, C480, C960 estas hipotezite de formoj de malmulte rondigitaj dudekedroj, je kelkaj nanometroj de amplekso.
