Dekduedro
| Dekduedro | |

| |

| |
| Klaku por rigardi turnantan bildon | |
| Speco | Regula pluredro |
| Vertica figuro | 5.5.5 |
| Bildo de vertico | 
|
| Bildo de reto | 
|
| Simbolo de Wythoff | 3 | 2 5 |
| Simbolo de Schläfli | {5,3} |
| Figuro de Coxeter-Dynkin | |
| Indeksoj | U23 C26 W5 |
| Simbolo de Bowers | Doe |
| Verticoj | 20 |
| Lateroj | 30 |
| Edroj | 12 |
| Edroj detale | 12{5} |
| χ | 2 |
| Geometria simetria grupo | Ih |
| Duedra angulo | arccos(-1/√5) ~= 116,56505° |
| Duala | Dudekedro |
| Bildo de duala | 
|
Dekduedro estas iu pluredro kun 12 edroj, sed kutime estas subkomprenata la regula dekduedro kiu estas platona solido komponita el 12 du regulaj kvinlateraj edroj, el kiuj tri kuniĝas je ĉiu vertico. Ĝi havas 20 verticojn kaj 30 randojn. Ĝia duala pluredro estas la dudekedro.
Areo kaj volumeno[redakti | redakti fonton]
La areo A kaj la volumeno V de regula dekduedro de randa longo a estas:
Karteziaj koordinatoj[redakti | redakti fonton]
Karteziaj koordinatoj de verticoj de dekduedro centrita je la nulo de koordinatoj:
- (±1, ±1, ±1)
- (0, ±1/φ, ±φ)
- (±1/φ, ±φ, 0)
- (±φ, 0, ±1/φ)
kie φ = (1+√5)/2 estas la ora proporcio. La latera longo estas 2/φ = −1+√5.
La duedra angulo de dekduedro estas 2 arctan(φ) aŭ proksimume 116,565º.
Geometriaj rilatoj[redakti | redakti fonton]
La regula dekduedro estas kvinlatera senpintigita kajtopluredro, la tria en malfinia aro de senpintigitaj kajtopluredroj kiu povas esti konstruita per senpintigo la du aksaj verticoj de kvinlatera kajtopluredro.
La steligoj de la dekduedro konsistigas trion el la kvar pluredroj de Keplero-Poinsot.
Situo de verticoj[redakti | redakti fonton]
La dekduedro komunigas ĝia situo de verticoj kun kvar nekonveksaj unuformaj pluredroj kaj tri unuformaj pluredraj kombinaĵoj.
Kvin kuboj adapti en, kun iliaj randoj kiel diagonaloj de la (dekduedra, dek-duedra) edroj, kaj kune ĉi tiuj konsistigi la regula pluredra kombinaĵo de kvin kuboj. Ekde du kvaredra povas adapti sur alternaj kubaj verticoj, kvin kaj dek kvaredra povas ankaŭ konformi dekduedro.
 Granda steligita dekduedro |
 Malgranda du-tritranĉa dudek-dekduedro |
 Du-tritranĉa dekdu-dekduedro |
 Granda du-tritranĉa dudek-dekduedro |
Kvin kuboj |
 Kvin kvaredroj |
 Dek kvaredroj |
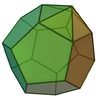
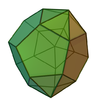
Solidoj de Johnson[redakti | redakti fonton]
Solidoj de Johnson surbaze de la dekduedro estas:
|

|

|
|
| Pligrandigita dekduedro (J58) | Tra-du-dupligrandigita dekduedro (J59) | Tra-unu-dupligrandigita dekduedro (J60) | Tripligrandigita dekduedro (J61) |
Dudekedro kaj dekduedro[redakti | redakti fonton]
Malgraŭ tio kiel ŝajnas, se dekduedro estas enskribita en sfero, ĝi okupas plion de la sfera volumeno (66,49%) ol dudekedro enskribita en la sama sfero (60,54%).
La alia dekduedroj[redakti | redakti fonton]
La vorto "dekduedro" estas uzata ankaŭ por la aliaj pluredroj kun 12 edroj, la plej rimarkindaj el ili estas la romba dekduedro kiu estas duala al la kubokedro (Arĥimeda solido) kaj okazas en naturo kiel formo de kristalo. La platona solida dekduedro povas nomiĝi kiel kvinlatera dekduedro aŭ regula dekduedro por distingi ilin.
Alia dekduedroj:
- Unuformaj pluredroj:
- Kvinlatera kontraŭprismo - 10 egallateraj trianguloj, 2 kvinlateroj
- Deklatera prismo - 10 kvadratoj, 2 deklateroj
- Solidoj de Johnson (kun regulaj edroj):
- Kvinlatera kupolo - 5 trianguloj, 5 kvadratoj, 1 kvinlatero, 1 deklatero
- Riproĉa dukojnosimilaĵo - 12 trianguloj
- Plilongigita kvadrata dupiramido - 8 trianguloj kaj 4 kvadratoj
- Apud-du-malkreskigita dudekedro - 10 trianguloj kaj 2 kvinlateroj
- Kongruaj neregulaj edroj (edro-transitivaj):
- Seslatera dupiramido - 12 izocelaj trianguloj, duala de seslatera prismo
- Seslatera trapezoedro - 12 deltoidoj, duala de seslatera kontraŭprismo
- Tripiramidigita kvaredro - 12 izocelaj trianguloj, duala de senpintigita kvaredro
- Romba dekduedro (menciita pli supre) - 12 romboj, duala de kubokedro
- Alia neregulaj edroj:
- Dekunulatera piramido - 11 izocelaj trianguloj kaj 1 dekunulatero
- Trapezo-romba dekduedro - 6 romboj, 6 trapezoj - duala de Triangula ortodukupolo
- Rombo-seslatera dekduedro aŭ Plilongigis Dekduedro - 8 romboj kaj 4 egallateraj seslateroj.
Diversaĵoj[redakti | redakti fonton]
- Se ĉiu rando de dekduedro estas 1 oma rezistancilo, la rezistanco inter najbaraj verticoj estas 19/30 omoj kaj inter kontraŭaj verticoj estas 7/6 omoj.[1]
- La regula dekduedro estas ofte uzita en rolludoj kiel 12-flankita ĵetpluredro ("d12" mallonge).
Vidu ankaŭ[redakti | redakti fonton]
- Senpintigita dekduedro
- Kvinpiramidigita dekduedro
- 120-ĉelo: regula plurĉelo (4-hiperpluredro) kies surfaco konsistas de 120 dekduedraj ĉeloj.
- Kvaruma dekduedro
- Kombinaĵo de dekduedro kaj dudekedro
| ||||||
Referencoj[redakti | redakti fonton]
- ↑ Klein, Duglaso J. (2002). “Resistance-Distance Sum Rules - Rezisto-Distancaj Sumaj Reguloj”, Croatica Chemica Acta (PDF) 75 (2), p. 633–649. Alirita 2006-09-30..
Eksteraj ligiloj[redakti | redakti fonton]
- La unuformaj pluredroj
- VRML modeloj:
- Regula dekduedro regula
- Romba dekduedro kvazaŭregula
- Deklatera prismo vertico-transitiva
- Kvinangula kontraŭprismo vertico-transitiva
- Seslatera dupiramido edro-transitiva
- Tripiramidigita kvaredro edro-transitiva
- seslatera trapezoedro edro-transitiva
- Kvinlatera kupolo regulaj edroj
- Eric W. Weisstein, Dekduedro en MathWorld.
- Eric W. Weisstein, Plilongigita dekduedro en MathWorld.



