Parta derivaĵo
En matematiko, parta derivaĵo de funkcio de kelkaj variabloj estas ĝia derivaĵo kun respekto al unu el ĉi tiuj variabloj, kiam la aliaj estas konstantaj, en kontrasto al la tuteca derivaĵo, en kiu al ĉiuj variabloj estas permesite varii.
La parta derivaĵo de funkcio kun respekto al la variablo x estas skribata kiel aŭ . La parto-derivaĵa simbolo, ∂ estas rondigita litero, por distingi ĝin de la normala rekta d de tuteco-derivaĵa simbolo. La skribmaniero estis prezentita de Adrien-Marie Legendre kaj ekhavis ĝeneralan akcepton post ĝia uzado de Carl Gustav Jakob Jacobi.
Partaj derivaĵoj estas aparte utilaj en vektora kalkulo kaj diferenciala geometrio.
Ekvacioj engaĝantaj partajn derivaĵojn de nekonataj funkciaj estas diferencialaj ekvacioj en partaj derivaĵoj, ili ofte estas uzataj en fiziko, inĝenierado kaj la aliaj kampoj.
Difino[redakti | redakti fonton]
La parta derivaĵo de funkcio f(x1,..., xn) kun respekto al xi je punkto (a1,...,an) estas difinita kiel limigo simile al ordinara derivaĵo:
En la esprimo pli supre, ĉiuj variabloj krom xi estas fiksitaj. Ĉi tiu elekto de fiksitaj valoroj difinas funkcion de unu variablo kaj laŭ la difino
Ĉi tiu esprimo ankaŭ montras ke kalkulado de partaj derivaĵoj reduktiĝas al kalkulado de unu-variablaj derivaĵoj.
Ekzemplo[redakti | redakti fonton]
Estu
- f(x, y) = x2 + xy + y2
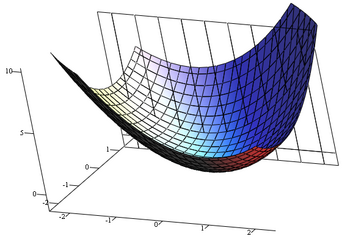 Grafikaĵo de x2 + xy + y2 |
Ekzemple oni deziru trovi partan derivaĵon de f je x je x=1, y=1.
Tiam, la funkcio devas esti konsiderata kiel funkcio nur de x kun y konstante egala al 1:
- fy=1(x) = x2 + x + 1
 Grafikaĵo de x2 + x + 1 |
Ĝia derivaĵo je x estas tiam normala (ne parta) derivaĵo kaj ĝi estas
kaj je la dezirata punkto
Eblas skribi formulojn pli ĝenerale, ne anstataŭigante tuj y per ĝia valoro, sed lasante ĝin kiel y kaj konsiderante ĝin kiel konstanto:
kaj je la dezirata punkto
La situacio tamen grave ŝanĝiĝas se y estas dependa de x. Se ekzemple y=2x-1 do
- f(x, y(x)) = x2 + xy(x) + (y(x))2 = x2 + x(2x-1) + (2x-1)2 = 7x2 - 5x + 1
La sama kiel antaŭe punkto x=1, y=1 konvenas por la dependeco y=2x-1, sed la derivaĵo tiam estas
Ĉi tio estas tuteca derivaĵo.
Propraĵoj[redakti | redakti fonton]
Eĉ se ĉiuj partaj derivaĵoj ∂f/∂xi ekzistas je donita punkto a, la funkcio ne nepre estas kontinua tie. Tamen, se ĉiuj partaj derivaĵoj ekzistas en najbaraĵo de a kaj estas kontinuaj tie, tiam f estas tutece diferencialebla en la najbaraĵo kaj la tuteca derivaĵo estas kontinua. En ĉi tiu okazo, oni diras ke f estas funkcio de klaso C1. Ĉi tio povas esti ĝeneraligita al vektoro-valoraj funkcioj (f : U → Rm) konsiderante la vektoran valoron laŭkomponente.
Partaj derivaĵoj de pli alta ordo[redakti | redakti fonton]
La parta derivaĵo ∂f/∂xi povas vidiĝi kiel la alia funkcio difinita sur la domajno U kaj povas denove esti parte diferencialita.
La nemiksita dua-ordaj parta derivaĵo rezultiĝas se diferencialado estas denove je la sama variablo:
Se la duan fojon preni derivaĵon je la alia variablo rezultiĝas la dua-orda miksita derivaĵo je du malsamaj variabloj xi kaj xj.
Se ĉiuj miksitaj dua-ordaj partaj derivaĵoj estas kontinuaj je la punkto (aŭ sur aro), la funkcia f estas de klaso C2 je tiu punkto (aŭ sur la aro) kaj en ĉi tiu okazo la partaj derivaĵoj povas esti interŝanĝitaj, alivorte la ordo de preno de derivaĵo - dekomence je xi poste je xj aŭ dekomence je xj poste je xi - ne gravas ĉar donas la saman valoron laŭ la teoremo de Clairaut:
Skribmaniero[redakti | redakti fonton]
Parta aŭ miksita derivaĵo de funkcio f(x, y, z) de ordo i+j+k kun ordo i je x, ordo j je y kaj ordo k je z estas skribata kiel
aŭ kiel
Se temas pri funkcioj de multaj variabloj kaj iuj el ĉi tiuj variabloj povas esti dependaj unu de la alia, povas esti necese al precizigi eksplicite kiu variabloj estas tenataj konstantaj. Ĉi tio povas esti esprimite kiel sekvas. Ekzemple parta derivaĵo de f kun respekto al x, tenante y kaj z konstantaj, estas
Gradiento[redakti | redakti fonton]
Estu skalaro-valora funkcio f(x1, ..., xn) kies domajno estas eŭklida spaco Rn (ofte R2 aŭ R3) kaj kiu havas partajn derivaĵojn ∂f/∂xj kun respekto al ĉiu xj. Tiam je donita punkto a=(a1, ..., an) ĉi tiuj partaj derivaĵoj difinas la vektoron
Ĉi tiu vektoro estas nomata kiel la gradiento de f je a. Se f estas diferencialebla je ĉiu punkto en iu domajno, tiam la gradiento estas vektoro-valora funkcio grad f kiu tiel difinas vektoran kampon.
Pli supre la vektoro estas skribita kiel linia vektoro, sed ofte ĝi estas konsiderata kiel kolumna vektoro


















