Frontoj de ebena ondo en tri-dimensia spaco .Ebena ondo estas ondo kun konstanta frekvenco. Ondaj frontoj de ebena ondo estas ebenaj frontoj, perpendikularaj al vektoro de faza rapido.
Tielaj ebenaj ondoj ne ekzistas en realo, ĉar ebena ondo komencigas en
−
1
{\displaystyle -{\mathcal {1}}}
+
1
{\displaystyle +{\mathcal {1}}}
«kvazaŭebena» . Se kvazaŭondo havas sufiĉan etendaĵon, do proksimume eblas opinii ĝin ebena.
Ekvacio de ajna ondo estas solvo de diferenciala ekvacio , nomiĝas «onda ekvacio» . Onda ekvacio por funkcio
A
{\displaystyle A}
Δ
A
(
r
→
,
t
)
=
1
v
2
∂
2
A
(
r
→
,
t
)
∂
t
2
{\displaystyle \Delta A({\vec {r}},t)={\frac {1}{v^{2}}}\,{\frac {\partial ^{2}A({\vec {r}},t)}{\partial t^{2}}}\,}
kie
Δ
{\displaystyle \Delta }
Laplaca operatoro ;
A
(
r
→
,
t
)
{\displaystyle A({\vec {r}},t)}
r
{\displaystyle r}
situa vektoro de nekonata punkto;
v
{\displaystyle v}
t
{\displaystyle t}
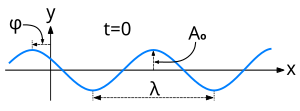
Animacia movado de ebena ondo. Ebena harmonia ondo rezultas je la jena ekvacio:
A
(
x
,
t
)
=
A
o
cos
(
k
x
−
ω
t
+
φ
0
)
{\displaystyle A(x,t)=A_{o}\cos \left(kx-\omega t+\varphi _{0}\right)\,}
kie
A
(
x
,
t
)
{\displaystyle A(x,t)}
x kaj tempo t ;
A
o
{\displaystyle A_{o}}
amplitudo ;
k
{\displaystyle k}
onda nombro ;
ω
{\displaystyle \omega }
Angula frekvenco ;
φ
0
{\displaystyle \varphi _{0}}
origina fazo . Ankoraŭ ondo priskribiĝas de ekvacioj
A
=
A
o
cos
(
2
π
(
x
λ
−
t
T
)
+
φ
0
)
{\displaystyle A=A_{o}\cos \left(2\pi \left({\cfrac {x}{\lambda }}-{\cfrac {t}{T}}\right)+\varphi _{0}\right)\,}
kie
A
=
A
o
cos
(
2
π
(
x
λ
−
f
t
)
+
φ
0
)
{\displaystyle A=A_{o}\cos \left(2\pi \left({\cfrac {x}{\lambda }}-ft\right)+\varphi _{0}\right)\,}
где
A
=
A
o
cos
(
2
π
λ
(
x
−
v
t
)
+
φ
0
)
{\displaystyle A=A_{o}\cos \left({\cfrac {2\pi }{\lambda }}(x-vt)+\varphi _{0}\right)\,}
где
Ĝenerale, ekvacio de ebena ondo enskribiĝas kiel
A
(
r
→
,
t
)
=
A
o
cos
(
(
k
→
,
r
→
)
−
ω
t
+
φ
0
)
{\displaystyle A({\vec {r}},t)=A_{o}\cos \left(({\vec {k}},{\vec {r}}\,)-\omega t+\varphi _{0}\right)\,}
kie
k
→
{\displaystyle {\vec {k}}}
onda vektoro , egala
k
n
→
{\displaystyle {k}{\vec {n}}\,}
kie
k
{\displaystyle k}
onda nombro ;
n
→
{\displaystyle {\vec {n}}}
normalo al onda fronto;
r
→
{\displaystyle {\vec {r}}}
situa vektoro de punkto;
(
k
→
,
r
→
)
{\displaystyle ({\vec {k}},{\vec {r}}\,)}
Skalara produto vektorojn
k
→
{\displaystyle {\vec {k}}}
r
→
{\displaystyle {\vec {r}}}
Tie ĉie kaj plu skalara produto estos simboliĝi tiele. Skribiĝas pli alte ekvicion povas skribiĝi en kompleksa formo:
A
(
x
,
t
)
=
A
o
e
i
(
k
x
−
ω
t
+
φ
0
)
.
{\displaystyle A(x,t)=A_{o}\,e^{i\left(kx-\omega t+\varphi _{0}\right)}.}
kaj ĝenerale
A
(
r
→
,
t
)
=
A
o
e
i
(
(
k
→
,
r
→
)
−
ω
t
+
φ
0
)
.
{\displaystyle A({\vec {r}},t)=A_{o}\,e^{i\left(({\vec {k}},{\vec {r}}\,)-\omega t+\varphi _{0}\right)}.}
Ĝusteco tiun formulon simple provas, uzas Eŭleran formulon .
El kompleksa formo de harmonia funkcio sekvas nocio de kompleksan amplitudon , egala
A
^
=
A
o
e
i
φ
0
.
{\displaystyle {\widehat {A}}=A_{o}e^{i\varphi _{0}}.}
Do
A
(
x
,
t
)
=
A
^
e
i
(
(
k
→
,
r
→
)
−
ω
t
)
.
{\displaystyle A(x,t)={\widehat {A}}\,e^{i\left(({\vec {k}},{\vec {r}}\,)-\omega t\right)}.}
modulo de funkcio egalas amplitudon, kaj argumento — origina fazo
φ
0
{\displaystyle \varphi _{0}}
Pli detalaj informoj troveblas en artikolo
Faza rapido .
La grupa rapido
v
g
{\displaystyle v_{g}}
v
g
=
∂
ω
∂
k
.
{\displaystyle v_{g}={\frac {\partial \omega }{\partial k}}.}
La faza rapido
v
ϕ
{\displaystyle v_{\phi }}
v
ϕ
=
ω
k
.
{\displaystyle v_{\phi }={\frac {\omega }{k}}.}
Se
A
(
x
,
t
)
=
A
o
cos
(
ω
t
−
k
x
+
φ
0
)
.
{\displaystyle A(x,t)=A_{o}\cos \left(\omega t-kx+\varphi _{0}\right).}
Apartiĝas en spaco malgranda volumento
Δ
V
{\displaystyle \Delta V}
∂
A
∂
t
{\displaystyle {\cfrac {\partial A}{\partial t}}}
∂
A
∂
x
{\displaystyle {\cfrac {\partial A}{\partial x}}}
Do tio volumenteto havas kineta energio
Δ
W
k
=
ρ
2
(
∂
A
∂
t
)
2
Δ
V
{\displaystyle \Delta W_{k}={\cfrac {\rho }{2}}\left({\cfrac {\partial A}{\partial t}}\right)^{2}\Delta V}
kaj potenciala energio deformiĝon
Δ
W
p
=
E
2
(
∂
A
∂
x
)
2
Δ
V
=
ρ
v
2
2
(
∂
A
∂
x
)
2
Δ
V
.
{\displaystyle \Delta W_{p}={\cfrac {E}{2}}\left({\cfrac {\partial A}{\partial x}}\right)^{2}\Delta V={\cfrac {\rho v^{2}}{2}}\left({\cfrac {\partial A}{\partial x}}\right)^{2}\Delta V.}
Totala energio egale
W
=
Δ
W
k
+
Δ
W
p
=
ρ
2
[
(
∂
A
∂
t
)
2
+
v
2
(
∂
A
∂
t
)
2
]
Δ
V
.
{\displaystyle W=\Delta W_{k}+\Delta W_{p}={\cfrac {\rho }{2}}{\bigg [}\left({\cfrac {\partial A}{\partial t}}\right)^{2}+v^{2}\left({\cfrac {\partial A}{\partial {t}}}\right)^{2}{\bigg ]}\Delta V.}
Denso de energio egale
ω
=
W
Δ
V
=
ρ
2
[
(
∂
A
∂
t
)
2
+
v
2
(
∂
A
∂
t
)
2
]
=
ρ
A
2
ω
2
sin
2
(
ω
t
−
k
x
+
φ
0
)
.
{\displaystyle \omega ={\cfrac {W}{\Delta V}}={\cfrac {\rho }{2}}{\bigg [}\left({\cfrac {\partial A}{\partial t}}\right)^{2}+v^{2}\left({\cfrac {\partial A}{\partial {t}}}\right)^{2}{\bigg ]}=\rho A^{2}\omega ^{2}\sin ^{2}\left(\omega t-kx+\varphi _{0}\right).}
Савельев И.В. // Курс общей физики — Часть 2. Волны. Упругие волны. // М.: Наука, 1988. // vol. 2. // p. 274-315.













































![{\displaystyle W=\Delta W_{k}+\Delta W_{p}={\cfrac {\rho }{2}}{\bigg [}\left({\cfrac {\partial A}{\partial t}}\right)^{2}+v^{2}\left({\cfrac {\partial A}{\partial {t}}}\right)^{2}{\bigg ]}\Delta V.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d932098511868ba0ef217492915b48d9a802cdc2)
![{\displaystyle \omega ={\cfrac {W}{\Delta V}}={\cfrac {\rho }{2}}{\bigg [}\left({\cfrac {\partial A}{\partial t}}\right)^{2}+v^{2}\left({\cfrac {\partial A}{\partial {t}}}\right)^{2}{\bigg ]}=\rho A^{2}\omega ^{2}\sin ^{2}\left(\omega t-kx+\varphi _{0}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/876102475200657f8a10bbef951a332d27309e62)