Arkimeda spiralo
Aspekto
| Ĉi tiu artikolo temas pri ebena kurbo (dudimensia objekto). Por pumpilo elpensita de Arkimedo rigardu la paĝon Arkimeda ŝraŭbo. |

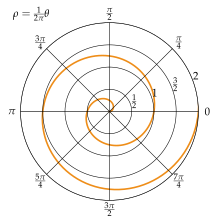
En geometrio, Arkimeda spiralo estas ebena kurbo, kies la polusa ekvacio estas:
- , kie:
- estas la angulo,
- a kaj b estas reelaj nombroj.
La tiel difinita spiralo malsamas de spiralo kun a= 0 per rotacio de angulo -b/a.
La Arkimeda spiralo estas la ebena kurbo trakurita de punkto kiu moviĝas kun konstanta rapideco sur rekto kiu turnas kun konstanta angula rapido ĉirkaŭ unu el siaj punktoj. Ekzemple la formo de la kanelo de gramofondisko estas Arkimeda spiralo.


