Dusekcanto
En geometrio, dusekco estas divido de io en du egalajn partojn, kutime per linio, kiu estas tiam nomata kiel dusekcanto. La plej ofte konsiderataj specoj de dusekcantoj estas dusekcanto de segmento kaj dusekcanto de angulo.
Dusekcanto de segmento pasas tra mezpunkto de la segmento. Aparte grava estas la perpendikulara dusekcanto de segmento, kiu, laŭ ĝia nomo, intersekciĝas kunverigas la segmento je ortoj. La perpendikulara dusekcanto de segmento ankaŭ havas propraĵon ke ĉiu de ĝiaj punktoj estas samdistancaj de finaj punktoj de la segmento. Pro tio randoj de figuro de Voronoi konsistas el segmentoj de ĉi tiaj linioj aŭ ebenoj.
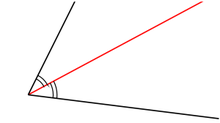
Dusekcanto de angulo dusekcanto dividas la angulon en du egalajn angulojn.
Angulo havas nur unu dusekcanton. Ĉiu punkto de angula dusekcanto estas samdistanca de la flankoj de la angulo. La ena parto de dusekcanto de angulo estas duonrekto aŭ segmento kiu dividas ĝin en du egalajn angulojn sur la sama flanko kiel la angulo mem. La ekstera parto de dusekcanto de angulo estas duonrekto aŭ segmento kiu dividas ĝin en du egalajn angulojn sur la transa flanko de la angulo.
En klasika geometrio, la dusekco estas farebla per cirkelo kaj liniilo, kaj ĝia ebleco dependas de ebleco desegni cirklojn de egalaj radiusoj de malsamaj centroj.

La segmento estas dusekcata per desegnado de intersekcantaj cirkloj de egala radiuso, kies centroj estas je finaj punktoj de la segmento. La linio difinata per du punktoj de komunaĵo de la cirkloj estas la perpendikulara dusekcanto de la originala segmento. Se linio kaj punkto sur ĝi estas donita, oni povas trovi perpendikularan dusekcanton per desegnade de sola cirklo kies centro estas je la donita punkto. La cirklo sekcas la linion je du novaj punktoj, kaj de ĉi tie la problemo reduktiĝas al dusekcado de la segmento difinita per ĉi tiuj du punktoj.

Por dusekci angulon, oni desegnas cirklo kies centro estas la vertico. La cirklo sekcas la angulon je du punktoj, po unu sur ĉiu flanko. Uzante ĉi tiujn punktojn kiel centroj, oni desegnas du intersekcantajn cirklojn de la sama amplekso. Du punktoj de komunaĵo de la cirkloj difinas rekton kiu estas dusekcanto de la angulo.
La pruvo de la praveco de ĉi tiuj du konstruoj estas honeste intuicia, fidanta je simetrio de la tasko.
Trisekco de angulo, kiu estas divido de la angulo en tri egalajn partojn, ne povas esti farita per nur cirkelo kaj liniilo.
La dusekcantoj de la anguloj de triangulo ĉiuj intersekciĝas en sola punkto, kiu estas centro de enskribita cirklo de la triangulo.

