Ekvacio de Arrhenius

La ekvacio de Arrhenius estas simpla, sed rimarkinde preciza, formulo por la influo de temperaturo al la rapideckonstanto de kemia reakcio. La nederlanda kemiisto J. H. van 't Hoff unue proponis la ekvacion en 1884. En 1889 la sveda kemiisto Svante Arrhenius klarigis teorion por ĝi. Nuntempe oni konsideras ĝin empiria rilato. Oni povas uzi ĝin por modeligi la temperaturvariadon de difuzaj koeficientoj, nombrado de truoj en kristaloj, rapido de rampfluo, kaj multaj aliaj procezoj kaŭzitaj de varmo.

Ekzistas empirio, ke por ĉiu 10 °C pliiĝo de temperaturo, la rapido de ajna reakcio duobliĝas aŭ triobliĝos. Tamen, tio kelkakaze malpravas.

Resumo

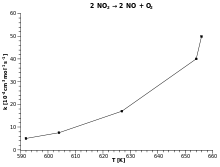
Ekzemplo: Malkombiniĝo de nitrogena dioksido
2 NO2 → 2 NO + O2
k kontraŭ T
ln(k) kontraŭ 1/T

La ekvacio de Arrhenius priskribas la rilaton inter la rapidokonstanto k de kemia reakcio kaj la temperaturo T (en kelvinoj) kaj la aktiviga energio E_a", kiel vidigita sube:

$k=Ae^{{-E_{a}}/{RT}}$

kie A estas la antaŭeksponenciala faktoro, kaj R estas la universala gaskonstanto. La unuoj de la antaŭeksponenciala faktoro estas identaj al tiuj de la rapidokonstanto kaj varias depende de la ordo de la reakcio. Se la reakcio estas unuaorda, ĝi havas la unuojn s⁻¹, kaj pro tio oni ofte nomas ĝin la frekvenca faktoro de la reakcio. Kiam la aktiviga energio esprimiĝas laŭ molekulaj unuoj anstataŭ molaj unuoj (ĵulo/molekulo anstataŭ ĵulo/molo) la konstanto de Boltzmann uzeblas anstataŭ la gaskonstanto. Por pliigi la rapidon de reakcio, oni povas aŭ pliigi la temperaturon aŭ malpliigi la aktivigan energion (ekzemple, per uzado de katalizilo).

When plotted in the manner described above, the value of the extrapolated "y-intercept" will correspond to $\ln(A)$, and the gradient of the line will be equal to $-E_{a}/R$.

En diagramo tia, kia vidiĝas en la apuda ekzemplo (dua bildo), la valoro de la eksterpolita y-intersekso egalas al $\ln(A)$, kaj la gradiento de la linio egalos al $-E_{a}/R$.

Sciante ke kinetikaj studoj kutime rilatas al mallarĝa amplekso de temperaturo, estas pravigeble supozi ke la aktiviga energio estas sendependa de temperaturo. Simile, sub vasta amplekso de praktikaj kondiĉoj, la malforta temperaturodependo de la frekvenca faktoro estas neglektinda kompare kun la temperaturodependo de la faktoro $\scriptstyle \exp(-E_{a}/RT)$, krom en la kazo de "senbaraj" difuzo-regataj reakcioj, ĉe kiuj la frekvenca faktoro dominas kaj estas rekte observebla.

Iuj aŭtoroj difinas modifitan ekvacion de Arrhenius, kiu eksplicitigas la temperaturodependon de la frekvenca faktoro. Se oni permesas arbitran temperaturodependon de la frekvenca faktoro, la priskribo de Arrhenius fariĝas trokompleta, kaj la kontraŭa problemo (t.e. kalkuli la frekvencan faktoron kaj la aktivigan energion por la eksperimentaj datumoj) fariĝas nekalkulebla. La modifita ekvacio kutime havas la formon:

$k=A(T/T_{0})^{n}e^{{-E_{a}}/{RT}}$

kie T₀ estas referenca temperaturo kaj permesas al n esti senunita potenco. Klare la origina esprimo de Arrhenius korespondas al la kazo kie n = 0. Statistike kalkulitaj rapidokonstantoj tipe valoras en la amplekso -1<n<1. Teoriaj analizoj liveras diversajn valorojn por n. Iu konstatis ke "ne estas praktikeble establi, sur la bazo de temperaturaj studoj de la rapidokonstanto, ĉu la antaŭvidita T^½-dependo de la antaŭeksponenciala faktoro observiĝas eksperimente." Tamen, se aldonaj pruvoj disponeblas, per teorio kaj/aŭ eksperimento (ekzemple densodependo), mankas malhelpo al decidigaj testoj de la ekvacio de Arrhenius.

Alia ofte uzata modifo estas la formo streĉita eksponenciala

$k=A\exp(-({\frac {-E_{a}}{RT}})^{\beta })$

kie β estas senunita numero de ordo 1. Oni konsideras tion eksperimenta modelo, sed ĝi povas havi teorian signifon, ekzemple montranta la ĉeeston de amplekso de aktivigaj energioj, aŭ en specialaj kazoj kiel la variampleksa saltado de Mott.

Prenante la naturan logaritmon de la ekvacio de Arrhenius liveras je:

$\ln(k)={\frac {-E_{a}}{R}}{\frac {1}{T}}+\ln(A)$

Do, kiam reakcio havas rapidokonstanton kiu kongruas kun la ekvacio de Arrhenius, diagramo de ln(k) kontraŭ T ^-1 donas rektan linion, kies gradiento kaj intersekco estas uzeblaj por kalkuli je E_a and A. Tiu procedo fariĝis tiel kutima en eksperimenta kinetiko, ke kemiistoj emas uzi ĝin por difini la aktivigan energion por reakcio. T.e. la aktiviga energio estas difinita esti -R-foje la gradiento de grafiko de ln(k) kontraŭ (1/T):

$\ E_{a}\equiv -R\left({\frac {\partial \ln k}{\partial ~(1/T)}}\right)_{P}$

Kinetika teorio klarigas la ekvacion de Arrhenius

Arrhenius argumentis ke por ke reakciantoj transformiĝu en produktojn, ili bezonas akiri minimuman energion, kiu nomiĝas la aktiviga energio E_a. Je absoluta temperaturo T, la proporcio de molekuloj kiuj havas kinetan energion pli ol E_a estas kalkulebla de la Maxwell-Boltzmann-a distribuo en statistika mekaniko, kaj ĝi montriĝas esti proporcia al $\ e^{\frac {-E_{a}}{RT}}$. La koncepto de aktiviga energio klarigas la eksponencialan naturon de la rilato, kaj iel ĉeestas en ĉiuj kinetaj teorioj (sube).

Kolizia teorio

Pli detalaj informoj troveblas en artikolo Kolizia teorio.

Unu ekzemplo venas el la "kolizia teorio" de kemiaj reakcioj, evoluigita de Max Trautz kaj William Lewis en la jaroj 1916-18. En tiu teorio, molekuloj supozeble reakcias se ili kolizias kun relativa kineta energio en la direkto de iliaj centroj kiu estas pli ol E_a. Tiel montriĝas esprimo tre simila al la ekvacio de Arrhenius, la eksponenciala dependo rilata al E_a, sed iuj opinias ke ĝi ne estas eksperimente pruvebla.

Transirstata teorio

Alia esprimo, simila al tiu de Arrhenius, aperas en la "transirstata teorio" de kemiaj rekacioj, evoluigita de Wigner, Eyring, Polanyi kaj Evans en la 1930-aj jaroj. Tio prenas diversajn formojn, sed unu plej ofta estas:

$\ k={\frac {k_{B}T}{h}}e^{-{\frac {\Delta G^{\ddagger }}{RT}}}$

kie ΔG^‡ estas la libera energio de Gibbs de aktivigo, k_B estas la konstanto de Boltzmann, kaj h estas la konstanto de Planck.

Unuavide, tio aspektas kiel eksponento multiplikita per faktoro kiu estas lineara de temperaturo. Tamen, oni devas memori ke libera energio ankaŭ dependas de temperaturo. La libera energio de aktivigo enhavas entropian termon, kiu multiplikiĝas per la absoluta temperaturo, kaj ankaŭ entalpian termon. Ambaŭ dependas de temperaturo, kaj ellaborante ĉiujn detalojn, oni fine atingas esprimon kiu denove prenas la formon de Arrhenius-tipa eksponento multiplikita de ete varianta funkcio de T. La preciza formo de la temperaturodependo dependas de la rekacio, kaj oni povas kalkuli ĝin uzante formulojn el statistika mekaniko, envolviĝante la partigajn funkciojn de la reakciantoj kaj de la aktivigita komplekso.

Notoj kaj referencoj

• Laidler, K. J. (1997) Chemical Kinetics,Third Edition, Benjamin-Cummings
• Laidler, K. J. (1993) The World of Physical Chemistry, Oxford University Press