Sfera trigonometrio

Unuaj formuloj de la sfera trigonometrio

Sfera ortangula triangulo

La sfera triangulo, ĉe kiu la angulo C estas orto

La sfera triangulo, ĉe ĝi la angula kromaĵo estas
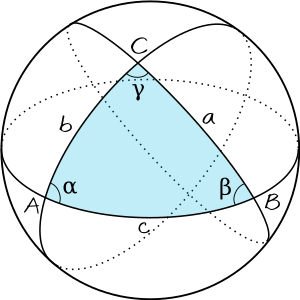
α + β + γ - π > 0

la formulo, kiu anstataŭas la teoremon de Pitagoro :

$\cos c = \cos a \cdot \cos b$

$\sin a = \sin c \cdot \sin \alpha$

$\sin b = \sin c \cdot \sin \beta$

$\cos \alpha = \cos a \cdot \sin \beta$

$\cos \beta = \cos b \cdot \sin \alpha$

$\cos c = \cot \alpha \cdot \cot \beta$

$\sin a = \tan b \cdot \cot \beta$

$\sin b = \tan a \cdot \cot \alpha$

$\cos \alpha = \tan b \cdot \cot c$

$\cos \beta = \tan a \cdot \cot c$

Ajna ortangula triangulo

$\frac{\sin \alpha}{\sin a} = \frac{\sin \beta}{\sin b} = \frac{\sin \gamma}{\sin c}$

La unua sfera leĝo de kosinusoj:

$\cos a = \cos b \cdot \cos c + \sin b \cdot \sin c \cdot \cos \alpha$

$\cos b = \cos a \cdot \cos c + \sin a \cdot \sin c \cdot \cos \beta$

$\cos c = \cos a \cdot \cos b + \sin a \cdot \sin b \cdot \cos \gamma$

La dua sfera leĝo de kosinusoj:

$\cos \alpha = -\cos \beta \cdot \cos \gamma + \sin \beta \cdot \sin \gamma \cdot \cos a$

$\cos \beta = -\cos \alpha \cdot \cos \gamma + \sin \alpha \cdot \sin \gamma \cdot \cos b$

$\cos \gamma = -\cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta \cdot \cos c$

• 

  Cirklo de Neper montras la rilatojn de partoj de orta sfera triangulo

Vidu ankaŭ

• Sfera geometrio
• Ĉefcirkla distanco
• Angulo
• Sfero
• Ĉefcirklo
• Malgranda cirklo
• Sfera leĝo de kosinusoj
• Formulo de duona rivolua sinuso

Eksteraj ligiloj

• http://mathworld.wolfram.com/SphericalTrigonometry.html
• http://mathworld.wolfram.com/SphericalTriangle.html
• http://www.rwgrayprojects.com/rbfnotes/trig/strig/strig.html