Sfera geometrio
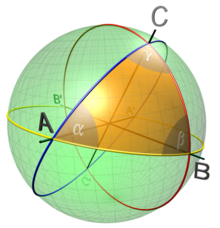
La sfera geometrio estas la geometrio de la dudimensia surfaco de sfero. Ĝi estas ekzemplo de neeŭklidaj geometrioj.
En ebena geometrio la bazaj konceptoj estas la punkto kaj la linio. En la sferp, la punktoj estas difinitaj en la kutima senco. La ekvivalentoj de la linioj ne estas difinitaj en la kutima senco de la "rekta linio" sed en la senco de "la plej mallongaj trajektorioj inter la punktoj", kio estas nomata geodezia linio. En la sfero geodeziaj estas la ĉefcirkloj, same kiel la aliaj geometriaj konceptoj estas difinitaj kiel en la ebena geometrio sed kun la linioj anstataŭataj per la ĉefcirkloj. Tiel, en sfera geometrio la anguloj estas difinitaj inter la ĉefcirkloj, rezulte en sfera trigonometrio kiu estu diferenca disde la ordinara trigonometrio en multaj aspektoj (por ekzemplo, la sumo de la internaj anguloj de triangulo superas la 180 gradojn).
La sfera geometrio estas la plej simpla modelo de la elipsa geometrio, en kiu difinita linio ne havas paralelan linion tra difinita punkto. Tio kontrastas kun la hiperbola geometrio, en kiu linio havas du paralelajn liniojn, kaj nefinitan nombron de ultra-paraleloj, tra difinita punkto.
La sfera geometrio havas gravajn praktikajn aplikojn en navigado kaj astronomio.
Samradiusajn cirklojn uzas la sfera geometrio simile, kiel rektojn la Eŭklida.[1] Sfer-geometrie, ĉiu sufiĉe longa linio kontaktas alian, do paraleloj ne ekzistas. Tiu geometrio estas utila modelo por la surfaco de sfero. Tial uzas ĝin oni en surtera navigacio.[2]
Notoj[redakti | redakti fonton]
- ↑ Geometría esférica (hispana lingvo, "Sfera geometrio") de la UNAM.
- ↑ Non-Euclidean Geometry (angla lingvo) en Liberal Arts Mathematics, fare de Galivan kaj Radke.
