Tri-dimensia spaco
Tri-dimensia spaco aŭ 3-dimensia spaco estas spaco, kiu havas tri dimensiojn.
En fiziko, la aktuala universo estas tri-dimensia spaco (kvankam ekzistas diversaj teorioj pri pli grandaj nombroj da dimensioj de la universo). La tri dimensioj estas ofte nomataj longo, larĝo kaj profundo, kvankam ĉiaj tri reciproke perpendikularaj direktoj povas servi kiel la tri dimensioj.
En fiziko, tri-dimensia spaco estas vidata kiel enigita en 4-dimensian spaco-tempon, nomatan kiel spaco de Minkowski (vidu plu en speciala relativeco). La ideo de spaco-tempo estas tio ke tempo estas perpendikularo al ĉiu el la tri spacaj dimensioj.
En matematiko, precipe en la ties branĉo analitika geometrio, oni priskribas ĉiun punkton de tri-dimensia spaco per tri koordinatoj.
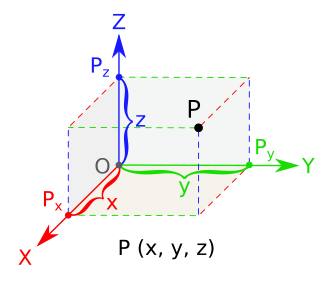
En tri-dimensia eŭklida spaco plejofte uzataj karteziaj koordinatoj, tri koordinataj aksoj estas donitaj, ĉiu perpendikulara al la aliaj du je la fonto, la punkto je kiuj ili inter kruciĝas. Ili estas kutime markita x, y, kaj z. Relativa al ĉi tiuj aksoj, la pozicio de ĉiu punkto en tri-dimensia spaco estas donita per ordita triopo de reelaj nombroj, ĉiu nombro donanta la signuman distancon de la punkto for de la fonto mezurita laŭ la donita akso, kiu estas egala al la distanco de la punkto de la ebeno difinita per du la aliaj aksoj.
Aliaj ofte uzataj koordinatosistemoj en tri-dimensia eŭklida spaco estas cilindraj koordinatoj kaj sferaj koordinatoj.
Alia matematika vojo de vidado de tri-dimensia spaco estas uzata en lineara algebro, kie la ideo de sendependeco estas grava. Spaco havas tri dimensiojn ĉar la longo de skatolo estas sendependa de ĝia larĝo kaj profundo. Do spaco estas tri dimensia ĉar ĉiu punkto en la spaco povas esti priskribita per lineara kombinaĵo de tri sendependaj koordinataj vektoroj. En ĉi tiu vido, la fizika spaco-tempo estas kvar dimensia ĉar tempo kiam iu evento okazas estas sendependa de ĝia situo en spaco.
Plejofte tri-dimensia eŭklida spaco (do, kun nula malrekteco) estas konsiderata, sed povas esti konsiderata ankaŭ tri-dimensia hiperbola spaco (kun negativa malrekteco), 3-sfero (kun pozitiva malrekteco) kaj la aliaj variantoj kun diversa malrekteco.
Tri-dimensia spaco havas iujn specifajn propraĵojn, kiuj distingan ĝin de spacoj de aliaj dimensioj. Ekzemple, nur en 3-dimensia spaco eblas nodo sur peco de linio [1]. En 3-dimensia spaco ekzistas vektora produto de vektoroj (en kutima aspekto). Multaj leĝoj de fiziko, kiuj enhavas inversan kvadratan leĝon, dependas de la 3-dimensieco [2].
La kompreno de tri-dimensia spaco de homoj estas opiniata kiel lernata dum infaneco uzante senkonsciajn konkludojn, kaj estas proksime rilatanta al mano-okula laboro. Ebleco percepti la mondon en tri dimensioj per vido estas profunda percepto.
Topologie, tri-dimensia spaco estas 3-sternaĵo.
Vidu ankaŭ
[redakti | redakti fonton]Referencoj
[redakti | redakti fonton]- ↑ Dale Rolfsen, Nodoj, kaj ligoj, Publish or Perish, Berkeley, 1976, ISBN 0-914098-16-0
- ↑ Brian Greene, La teksaĵo de la kosmo, Random House, Novjorko, 2003, ISBN 0-375-72720-5
