Angula rapido

En fiziko, la angula rapido estas vektora kvanto (pli detale, pseŭdovektoro) kiu priskribas la rapidon de turnado kaj la orientiĝon de la akso ĉirkaŭ kiu la turnado okazas. La SI-mezurunuo de angula rapido estas radianoj dum sekundo. Ĝi povas esti mezurita ankaŭ en aliaj mezurunuoj, tiaj kiel gradoj en sekundo, gradoj por horo, turnoj en minuto.
Ĝia grando estas la turna rapido. Angula rapido estas kutime prezentita per la simbolo omego (Ω aŭ ω). La direkto de la vektoro de la angula rapido estas perpendikulara al la ebeno de turnado, en direkto kiu estas kutime precizigita per la regulo de dekstra ŝraŭbo.
Angula rapido estas propraĵo de punkta partiklo kaj propraĵo de solido. La du okazoj estas malsamaj. Se konsideri iun solidon kaj trovi ĝian angulan rapidon, kaj ankaŭ preni iun partiklon de la solido kaj trovi ĝian angulan rapidon, do la rezultoj estos ĝenerale malsamaj. La rezultoj estos la samaj nur se la angulan rapidon de la partiklo konsideri respektive al la plej proksima al la partiklo punkto sur la turnada akso de la solido.
La angula rapido de partiklo[redakti | redakti fonton]
Du dimensioj[redakti | redakti fonton]

La vektora rapido v de la partiklo havas komponanto laŭ la radiuso (radiusa komponanto, v∥) kaj komponanta perpendikulare al la radiuso (tanĝanta komponanto, v).
Radiusa moviĝo ne produktas turnadon de la partiklo relative al la fonto, tiel por trovado de la angula rapido la paralelo (radiusa) komponanto povas esti neglektita. La turnado estas plene produktita per la tanĝanta moviĝo, komponanto per kiu la partiklo moviĝas laŭ cirklo kun centro en la fonto, kaj la angula rapido estas plene difinita per la perpendikularo (tanĝanta) komponanto.
La kurzo de ŝanĝo de la angula pozicio de la partiklo estas rilatanta al la tanĝanta rapido kiel:
Estu θ la angulo inter vektoroj v∥ kaj v, aŭ ekvivalente la angulo inter vektoroj r kaj v, tiam:
Kombinante la pli suprajn du ekvaciojn kaj difinante la angulan rapidon kiel ω=dφ/dt rezultas:
En du dimensioj la angula rapido estas sola nombro. Sola nombro kiu havas ne direkton estas skalaro aŭ pseŭdoskalaro, la diferenco estas en tio ke skalaro ne ŝanĝas sian signo kiam la koordintosistema estas anstataŭigita per refliktita (ekzemple x kaj y aksoj estas interŝanĝita, aŭ unu el la aksoj estas inversigita je direkto), kaj pseŭdoskalaro ŝanĝas sian signo en ĉi tiu okazo. Tiel la angula pozicio kaj ankaŭ la angula rapido estas pseŭdoskalaro. La pozitiva direkto de turnado estas prenita, per konvencio, kiel direkto de la pozitiva x akso al la pozitiva y akso. Se la aksoj estas interŝanĝitaj, sed la senco de turnado ne, tiam la signo de la angulo de turnado, kaj pro tio ankaŭ signo de la angula rapido, estas ŝanĝita.
Grava noto estas ke la angula rapido de partiklo dependas de elekto de la fonto.
Tri dimensioj[redakti | redakti fonton]
En tri dimensioj, la angula rapido estas ĝenerale vektoro, aŭ, pli precize, pseŭdovektoro. Ĝi havas ne nur grandecon, sed ankaŭ direkton. La grandeco estas angula rapido kiel en 2-dimensioj, kaj la direkto priskribas la rotacian akson. La dekstra ŝraŭba regulo indikas la pozitiva direkton de la angula rapida pseŭdovektoro:
- Se objekto turniĝas laŭhorloĝnadle, la turna vektoro montras for de la observanto.
 Angula rapido (blua montrilo) je unu unuo laŭhorloĝnadle |
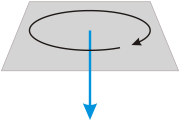 Angula rapido (blua montrilo) je 3/2 unuoj laŭhorloĝnadle |
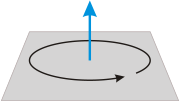 Angula rapido (blua montrilo) je unu unuo kontraŭhorloĝnadle |
Same kiel en la 2-dimensia okazo, partiklo havas komponanton de ĝia vektora rapido laŭ la radiuso de la fonto al la partiklo kaj komponanton perpendikulare al la radiuso. La kombinaĵo de la fonta punkto kaj la perpendikulara komponanto de la vektora rapido difinas la ebenon de turnado en kiu konduto de la partiklo aspektas same kiel en la 2-dimensia okazo. La rotacia akso estas tiam rekto perpendikularo al ĉi tiu ebeno, kaj ĉi tiu akso difinas direkton de la angula rapida pseŭdovektoro, kaj ĝia grandeco estas la sama kiel la absoluta valoro de la pseŭdoskalara valoro en la 2-dimensia okazo. Estu unuobla vektoro kiu montras same kiel la angula rapida pseŭdovektoro. La angula rapido povas esti skribita en maniero simila al tiu por du dimensioj:
kiu, laŭ la difino de la vektora produto, povas esti skribita:
Pli altaj dimensioj[redakti | redakti fonton]
Ĝenerale, la angula rapido en n-dimensia spaco estas la tempa derivaĵo de la angula delokiga tensoro kiu estas deklivo-simetria tensoro de rango 2. Ĉi tiu tensoro havas n(n-1)/2 sendependajn komponantojn kaj ĉi tiu nombro estas la dimensio de la alĝebro de Lie de la grupo de Lie de turnadoj de n-dimensia ena produta spaco. Ĝuste en tri dimensia spaco n=3 kaj do n(n-1)/2=3 kaj do angula rapido povas esti prezentita per vektoro ĉar la kvanto de sendependaj komponantoj egalas al la kvanto de dimensioj de spaco.
Angula rapido de solido[redakti | redakti fonton]
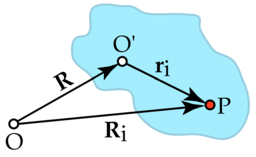
Por konsideri moviĝon de solido, ĉi tie estas konsiderita koordinatsistema kiu estas fiksita kun respekto al la solido, kaj estas studataj la koordinataj transformoj inter ĉi tiu koordinatosistemo kaj la fiksita laboratoria koordinatosistemo. Fonto de la laboratoria koordinatosistemo estu punkto O, fonto de la solida koordinatosistemo estu O' kaj la vektoro de O al O' estas R. Partiklo i en la solido situas je punkto P kaj la vektora pozicio de ĉi tiu partiklo estas Ri en la laboratoria koordinatosistemo, kaj ri en la solida koordinatosistemo. Tiel:
La difinanta karakterizo de solido estas ke distanco inter ĉiu duo da punktoj de solido estas neŝanĝanta kun tempo. Ĉi tio signifas ke longo de vektoro ri estas neŝanĝanta kun tempo. Per la eŭlera turnada teoremo, oni povas anstataŭigi la vektoron ri per kie W estas 3×3 turnada matrico kaj estas pozicio de la partiklo en tempo t=0. Ĉi tiu anstataŭo estas utila, ĉar tiam estas la turnada matrico W kiu ŝanĝiĝas kun tempo kiam la solido turnas ĉirkaŭ punkta O' , sed la referenca vektoro ne ŝanĝiĝas. La pozicio de la partiklo estas do:
Preno de la tempa derivaĵo donas vektoran rapidon de la partiklo:
kie Vi estas la vektora rapido de la partiklo (en la laboratoria koordinatosistemo),
- V estas la vektora rapido de O' (la fonto de la solido).
Pro tio ke estas turnada matrico ĝia inverso estas ĝia transpono. Tiel I=WTW kie I estas la 3×3 identa matrico kaj do:
Oni prenu la tempan derivaĵon de :
- I=WWT
Pro tio ke ĝenerale (AB)T = BTAT:
Tiel estas negativa de sia transpono kaj do kontraŭsimetria 3×3 matrico. Oni povas pro tio preni ke ĝia dualo estas 3 dimensia vektoro. estas nomata kiel la angula rapida tensoro. Se preni la dualon de ĉi tiu tensoro, matrica multipliko estas anstataŭigita per la vektora produto. Ĝia dualo estas nomata kiel la angula rapida pseŭdovektoro ω
Enenmetante ω en la esprimo de vektora rapido pli supre rezultas:
La turnada matrico ne dependas de elekto de la punkto O' kaj i, tiel la angula rapido de la solido estas la sama, kaj la angula rapido estas sendependa de elekto de la fonto de la solida sistemo aŭ de la laboratoria koordinatosistemo. En aliaj vortoj, angula rapido estas fizike reala kvanto kiu estas propraĵo de la solido, sendependa de elekto de koordinatsistemoj. Estas ofte oportune elekti la centron de maso de la solido kiel la fonton de la solida sistemo, pro tio ke en ĉi tiu okazo okazas konsiderebla plisimpligo de esprimo por la angula movokvanto de la solido.
Tiel la vektora rapido de punkto en solido povas esti dividita en du erojn - la vektora rapido de referenca punkto fiksita en la solido plus la vektora produto de la angula rapido de la solido kun respektiva pozicio de la partiklo al la referenca punkto. Ĉi tiu angula rapido estas la spina angula rapido de la solido, kiu estas malsama de la angula rapido de la referenca punkta O' ĉirkaŭ la fonto O.
Vidu ankaŭ[redakti | redakti fonton]
- Angula akcelo
- Angula frekvenco
- Angula movokvanto
- Solida dinamiko
- Turnada grupo SO(3)
- Alĝebro de Lie
- Perpendikulara grupo
- Izometrio
Eksteraj ligiloj[redakti | redakti fonton]
- angle Turnadoj kaj angula momanto sur la klasika mekanika paĝo de la TTT-ejo de John Baez, aparte demandoj 1 kaj 2. Ankaŭ pri multdimensia okazo.





















![{\displaystyle {\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)
