Tensoro
En matematiko kaj fiziko, tensoro estas geometria ento etendanta la komprenaĵojn de skalaro, vektoro, kvadrata matrico kaj dulineara formo.
Multaj fizikaj kvantoj estas nature ne vektoroj mem, sed rilatoj inter unu aro de vektoroj kaj la alia. Ekzemplo estas la streĉo, kiu prenas unu vektoron kiel enigo kaj produktas alian vektoron kiel eligo kaj tiel priskribas interrilaton inter la eniga kaj eliga vektoroj.
Plejparto de parametroj de substanco, kutime priskribataj per skalaroj, iĝas tensoroj se la substanco estas malizotropa. Inter la parametroj estas elektra rezistanco, varma rezistanco, dielektra permeableco, rapido de sono.
Ĉar ili esprimas interrilatojn inter vektoroj, tensoroj mem estas sendependaj de aparta elekto de koordinatosistemo. Eblas prezenti tensoron per ekzamenado de tio kion ĝi faras al koordinata bazo aŭ kadro de referenco; la rezultantaj kvantoj estas tiam organizitaj kiel multdimensia d×d×...×d tabelo de nombraj valoroj, kie d estas dimensio de la spaco. La koordinata sendependeco de tensoro tiam prenas la formon de kunvarianca transforma leĝo kiu donas rilatojn de la tabelo komputita en unu koordinatosistemo al tiu komputita en alia koordinatosistemo. La ordo (aŭ grado) de tensoro estas la dimensinombro de la tabelo bezonata por prezenti ĝin. Tial skalaro estas nulo-orda tensoro: ĝia grandeco estas ĝia sola komponanto, tiel ĝi povas esti prezentita kiel 0-dimensia tabelo. Vektoro estas unu-orda tensoro, estante prezentebla en koordinatoj kiel 1-dimensia tabelo de komponantoj. Kvadrata matrico estas du-orda tensoro, estante prezentebla kiel 2-dimensia tabelo. Kaj tiel plu: ordo-k tensoro povas esti prezentita kiel k-dimensia tabelo de komponantoj. La ordo estas la kvanto de indicoj necesaj por precizigi ĉiun apartan komponanton de tensoro.
La sendependeco de tensoro mem de la koordinatosistemo videblas surbaze de vektoro kiel simpla ekzemplo. En la alia koordinatosistemo, la vektoro kiel geometria ento estas la sama, sed la nombroj kiuj ĝin prezentas estas la aliaj.
Difinoj[redakti | redakti fonton]
Estas du manieroj de difinado de tensoroj:
- La kutima fizika maniero de difinado de tensoroj, per objektoj kies komponantoj konvertiĝas laŭ certaj reguloj, prezentante la ideojn de kunvarianca aŭ kontraŭvarianca transformoj.
- La kutima matematika maniero, kiu engaĝas difinon de certaj vektoraj spacoj kaj ne fiksadon de iuj koordinatosistemoj ĝis kiam bazoj prezentataj kiam bezonataj. Kontraŭvariancaj vektoroj, ekzemple, povas ankaŭ esti priskribitaj kiel 1-formoj, aŭ kiel la eroj de la dualoj al la kunvariancaj vektoroj.
Valento[redakti | redakti fonton]
La tabelaj indicoj estas distingitaj kiel estantaj kontraŭvariancaj (supraj indicoj) aŭ kunvariancaj (subaj indicoj), dependante de la speco de transformaj propraĵoj. La valento de aparta tensoro estas la kvanto kaj speco de la tabelaj indicoj; tensoroj kun la sama ordo sed malsama valento ne estas, ĝenerale, identaj. Tamen, ĉiu donita kunvarianca indico povas esti konvertita en kontraŭvariancan, kaj reen, per apliko de la metrika tensoro. Ĉi tiu operacio estas ĝenerale sciata kiel altigo kaj malaltigo de indicoj.
Tensoro de valento (n, m) super d-dimensia vektora spaco V estas ero de tensora produto de m spacoj V kaj n konjugitaj spacoj V*. V* estas spaco de linearaj funkcioj (1-formoj) sur V.
La sumo n+m estas ordo de la tensoro. Tensoro de valento (n, m) estas n foje kunvarianca kaj m foje kontraŭvarianca.
Tensoro kiel plurlineara funkcio[redakti | redakti fonton]
Kunvarianca tensoro de valento (1, 0) estas lineara funkcio (1-formo).
Kunvarianca tensoro τ de valento (n, 0) povas esti konsiderata kiel funkcio de n vektoraj argumentaj, kiu estas lineara je ĉiu el siaj argumentoj , kio estas ke por ĉiu konstanto c
Simile, tensoro τ de valento (n, m) povas esti konsiderata kiel funkcio de n vektoroj kaj m kunvektoroj, kiu estas lineara je ĉiu el siaj argumentoj:
Ekzemploj[redakti | redakti fonton]
- Tensoro de valento (0, 0) estas skalaro.
- Kontraŭvarianca tensoro de valento (0, 1) estas vektoro, ero de V.
- Kunvarianca tensoro de valento (1, 0) estas ero de V*, aŭ lineara funkcio (1-formo) sur V.
- Kunvarianca tensoro de valento (2, 0) estas dulineara formo.
- Tensoro de valento (1, 1) estas lineara operatoro A : V → V aŭ A : V* → V* .
- Volumena formo sur n-dimensia spaco estas malsimetria n foje kunvarianca tensoro de valento (n, 0)
- Rimana kurbeco en natura varianto estas , tensoro de valento (3, 1).
Kiel ekzemplo de malsameco de la transformo kun ŝanĝo de koordinatoj, estu x kaj y koordinataj prezentoj de vektoroj. En la alia koordinatosistemo ili estas prezentataj kiel x' = Gx kaj y' = Gy . Estu lineara operatoro A, tiam povas esti egaleco y=Ax . Tiam:
- G−1y' =AG−1x'
- y' =GAG−1x'
kaj do
- y' = A' x' kie A' = GAG−1
Estu dulineara formo prezentata kiel b = xTBy . Tiam
- b = (G−1x' )TBG−1y'
- b = x' T(G−1)TBG−1y'
- b = x' TB' y' , kie B' = (G−1)TBG−1
De ĉi tie videblas ke la konvertaj reguloj por A kaj B estas malsamaj.
Tensoro estas tabelo de komponantoj kune kun certa leĝo de transformado de la komponantoj en okazo de ŝanĝo de koordinatosistemo. Tiel ne ĉiu tabelo de nombroj, eĉ de taŭgaj ampleksoj, estas tensoro.
Ekzemploj de ne-tensoroj:
- Tabelo de pli ol unu nombro, kiuj nombroj ne dependas de koordinatosistemo, ne estas tensoro.
- Subaro de komponantoj de tensoro ĝenerale ne estas tensoro de pli malgranda ordo.
- Se nombroj de la tabelo dependas de koordinatosistemo, kaj en unu koordinatosistemo ne ĉiu el ili estas nulo, kaj en la alia koordinatosistemo ili ĉiuj estas nuloj, do ĉi tio ne estas tensoro.
- Estas objektoj kiu estas similaj al tensoroj, kaj por kiuj eĉ havas sencon iuj tensoraj operacioj, kiel kunfaldo, sed kiuj tamen ne estas tensoroj:
- Jakobiaj matricoj priskribantaj ŝanĝon de koordinatoj ne estas tensoroj.
Komponantoj de tensoro[redakti | redakti fonton]
Estu en la spaco V bazo , kaj estu duala bazo en konjugita spaco V* (kio estas ke , kie estas delto de Kronecker).
Tiam en tensora produto de spacoj estas bazo
Se difini tensoron kiel plurlineara funkcio, do ĝiaj komponantoj estas difinataj per valoroj de la funkcio sur la bazo :
Tiam la tensoron eblas skribi kiel lineara kombinaĵo de bazaj tensoraj produtoj:
Ekzemple, prezento de dufoje kunvarianca tensoro h estas:
Simetrioj[redakti | redakti fonton]
Estadas tensoroj kun certaj propraĵoj de simetrio.
Simetria je du indicoj estas tensoro tia ke
aŭ en komponantoj
Malsimetria je du indicoj estas tensoro tia ke
aŭ en komponantoj
Simetrieco kaj malsimetrieco estas ne nepre pri najbaraj indico, sed pri ajnaj. Tamen la du indicoj devas esti de la sama speco, ambaŭ kunvariancaj aŭ ambaŭ kontraŭvariancaj. Simetrio je kunvarianca kaj kontraŭvarianca indicoj ofte ne estas de intereso ĉar ĝi perdiĝas kun ŝanĝo de koordinatosistemo. Tamen ĉe ekzisto de metrika tensoro ĉi tiu kondiĉo povas esti forprenita.
Simetrieco kaj malsimetrieco povas esti ĝeneraligitaj al pli ol du indicoj de unu tensoro. Tiam simetria tensoro ne ŝanĝiĝas post ĉiu permuto de la indicoj; malsimetria tensoro ne ŝanĝiĝas post ĉiu para permuto de la indicoj kaj ŝanĝias signumon post ĉiu nepara permuto de la indicoj.
Operacioj kun tensoroj[redakti | redakti fonton]
Ĉefaj tensoraj operacioj estas adicio kaj kunfaldo. La adicio estas laŭkomponanta, same kiel ĉe matricoj. La kunfaldo estas ĝeneraligo de matrica multipliko. Multipliko de tensoro je nombro povas esti konsiderata kiel okazo de kunfaldo, ĝi estas multipliko de ĉiu komponanto per la nombro.
Kunfaldo de unu tensoro estas specifa operacio kiu malpligrandigas valenton de ĝi. Ĝi estas kalkulata per sumigo laŭ du indicoj, unu supra kaj unu suba, ekzemple:
Ofte la rezulto de kunfaldo estas signifata per la sama litero, sed kun malpli multaj indicoj.
Tensora produto estas difinita sen limigoj je valento de la fontaj tensoroj. Produto de tensoro A de valento (n, m) kaj tensoro B de valento (n', m') estas tensoro P=A⊗B de valento (n+n', m+m'), kies komponantoj estas produtoj de respektivaj komponantoj de la fontaj tensoroj. Ekzemple:
aŭ
aŭ
Kunfaldo de du tensoroj estas kunfaldo de produto de la tensoroj. Ĝi estas kalkulata per sumigo laŭ du indicoj, unu supra kaj unu suba, de malsamaj fontaj tensoroj:
Kunfaldo estas lineara je ĉiu el siaj argumentoj. Tiel kunfaldo kun tensoro estas lineara bildigo de tensora spaco al tensora spaco, la sama aŭ la alia.
Kunfaldo de ajnaj tensoroj, se rezulte restas neniu indico, estas skalaro. Ĝi ne dependas de elekto de koordinatosistemo. Tiel spuro estas okazo de plena kunfaldo de unu tensoro.
Kunfaldo de vektoro kun tensoro de valento (1, 1) estas apliko al la vektoro de la lineara operatoro, priskribata per la tensoro, kaj estas reale la samo kiel multipliko de vektoro kaj matrico:
Kunfaldo de du tensoroj de valento (1, 1) redonas komponaĵon de la linearaj operatoroj, priskribataj per la tensoroj, kaj estas reale la samo kiel matrica multipliko de du kvadrataj matricoj:
Simetrigo kaj malsimetrigo estas konstruo de tensoro de la sama valento kun certa simetria propraĵo. Ekzemple, simetrigo de tensoro estas simetria tensoro , malsimetrigo de ĝi estas malsimetria tensoro . Pli ĝenerale simetrigo je n indicoj estas
kaj malsimetrigo estas:
kie σ estas ĉiu permutoj de indicoj ;
- sign(σ) estas signumo de permuto σ, kiu egalas al 1 por para kaj -1 por nepara permuto.
La simetrigo kaj malsimetrigo povas esti faritaj je nur parto de havataj indicoj de la tensoro.
Ejnŝtejna skribmaniero[redakti | redakti fonton]
Ejnŝtejna skribmaniero estas konvencio por skribado de formuloj kun tensoroj sen skribado de sumadaj signoj. Ĝi fidas sur la ideo ke ĉiu ripetita indico estas sumita super: se la indico i estas uzata dufoje en donita termo de tensora esprimo, ĉi tio signifas ke la valoroj devas esti sumitaj super i. Kelkaj malsamaj paroj de indicoj povas esti sumitaj tiamaniere.
Ekzemple anstataŭ
estas skribata
Aplikoj[redakti | redakti fonton]
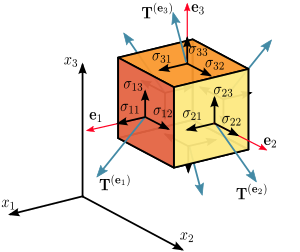
Iuj el la plej gravaj aplikoj estas en kontinuaĵa mekaniko. La streĉoj en solida korpo aŭ fluaĵo estas priskribitaj per tensoroj. La streĉa tensoro kaj tensia tensoro estas ambaŭ tensoroj de ordo 2, kaj estas rilatantaj en ĝenerala lineara elasta materialo per elasteca tensoro de ordo 4. Detale, la 2-a orda tensoro priskribanta streĉon en 3-dimensia solida objekto havas komponantojn kiu povas esti oportune prezentataj kiel 3×3 tabelo. La tri karteziaj edroj de kubo-formita infinitezima volumeno de la solido estas ĉiu kun iu donita forto. La fortaj vektoraj komponantoj estas ankaŭ tri en kvanto (estante en tri-spaco). Tial, 3×3, aŭ 9 komponantoj estas postulitaj por priskribi la streĉon je ĉi tiu kubo-formita infinitezima parto (kiu povas nun esti traktata kiel punkto). Tial, 2-a orda tensoro estas bezonata.
Se aparta surfaca ero en la materialo estas eltranĉita, la materialo sur unu flanko de la surfaco aplikos forton transe. Ĝenerale, ĉi tiu forto estos ne nepre perpendikulara al la surfaco, sed ĝi dependos de la orientiĝo de la surfaco en lineara maniero. Ĉi tio estas priskribita per tensoro de speco (2, 0), lineara elasteco, aŭ pli detale per tensora kampo de speco (2, 0) pro tio ke la streĉoj povas ŝanĝiĝi de punkto al punkto.
Kiel la alia ekzemplo kosideru la elektran konduktivecon σ. Malizotropa materialo, kiel kristalo, povas esti kvazaŭ multaj paralelaj bone konduktantaj dratoj en malbone konduktanta ĉirkaŭaĵo.
Elektra konduktiveco laŭlonge de la dratoj estu σ1. Se la dratoj estas kunpremitaj en unu direkto perpendikulare al la longo, la konduktiveco laŭ la kunpremo kaj perpendikulare al la kunpremo povas esti malsamaj. Tiel konduktiveco laŭ la kunpremo perpendikulare al la longo de la dratoj estu σ2 kaj konduktiveco perpendikulare al la kunpremo perpendikulare al la longo de la dratoj estu σ3.
Ne evidenta fakto pri ĉi tio estas ke nepre ekzistas 3 reciproke perpendikularaj direktoj, por kiuj la vektora kurenta denseco j kaj vektora elektra kampo E estas interrilatantaj per multipliko je skalara faktoro, do ili estas paralelaj. En la ekzemplo, la 3 direktoj estas tiuj por kiuj estas la konduktivecoj σ1, σ2 kaj σ3.
Ĉiun vektoron eblas malkomponigi je komponantoj je ĉi tiuj 3 direktoj
kaj la valoroj de la kurenta denseco en ĉiu el la direktoj tiam estas
Tiam por ĉiu vektoro E, ne paralela al la 3 direktoj, la vektoroj E kaj j povas esti ne paralelaj.
Trairante al karteziaj koordinataj kies aksoj ne koincidas kun la direktoj de σ1, σ2 kaj σ3, necesas multipliki la vektorojn je certaj turnadaj matricoj, kaj do en ĝeneralaj karteziaj koordinataj la interrilato havas formon
kaj tiel σ estas tensoro de la 2-a ordo, kiu estas kiel kvadrata matrico, lineara operatoro donanta vektoron j por ĉiu donita vektoro E. Ĉi tie la koordinatoj estas perpendikularaj inter si kaj de la sama skalo, do ne estas diferenco inter subaj kaj supraj indicoj.
Plu, denseco de varmeca povumo pro la kurento w egalas al la skalara produto , kaj ĝi povas esti skribita:
aŭ
kie ρ estas la elektra rezistanco, inverso de σ. Ĉi tio montras la alian okazon de tesoro, kiu estas kvadrata formo, konvertanta vektoron en skalaron, kun tio ke kvadrata formo estas dulineara forma uzata kun la sama vektoro por ambaŭ argumentoj.
Eksteraj ligiloj[redakti | redakti fonton]
- [1] Шарипов Р. А. Быстрое введение в тензорный анализ. - БашГУ. - Rapida enkonduko al tensora analizo de R. A. Sharipov, plena teksto en dosierformo PDF
- Diskuto pri la diversaj manieroj de instruado de tensoroj, kaj kandidatigoj de lernolibroj Arkivigite je 2005-11-04 per la retarkivo Wayback Machine
- Enkonduko al vektoroj kaj tensoroj, volumo 1: Lineara kaj Plurlineara Algebro de Ray M. Bowen kaj C. C. Wang.
- Enkonduko al vektoroj kaj tensoroj, volumo 2: Vektora kaj Tensora Analizo de Ray M. Bowen kaj C. C. Wang.
- Che cos'è un tensore Arkivigite je 2008-06-12 per la retarkivo Wayback Machine
- Enkonduko al tensoroj de Joakim Strandberg.
- An Enkonduko al Tensoroj por Studentoj de Fiziko kaj Inĝenierado, eldonita de NASA, plena teksto en dosierformo Arkivigite je 2010-06-26 per la retarkivo Wayback Machine PDF
- Englisches Online Buch über Tensoren und ihre Anwendung von Heinbockel
- Über Tensoren, Matrizen und Pseudovektoren, plena teksto en dosierformo Arkivigite je 2013-04-18 per la retarkivo Wayback Machine PDF
- Zur Visualisierung von Vektoren[rompita ligilo]
- Ricci, Gregorio; Levi-Civita, Tullio (Marto 1900). Méthodes de calcul différentiel absolu et leurs applications. Mathematische Annalen 54 (1–2) 125–201. Springer. COI:10.1007/BF01454201.
- Eric W. Weisstein, Tensoro en MathWorld.
- Акивис М. А., Гольдберг В. В. Тензорное исчисление. - Moskvo: eldonejo Наука, 1969, plena teksto en dosierformo DjVu
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления (9-е издание). - Moskvo: eldonejo Наука, 1965, plena teksto en dosierformo DjVu
- Мак-Коннел А. Дж. Введение в тензорный анализ с приложениями к геометрии, механике и физике. - Moskvo: eldonejo Физматлит, 1963, plena teksto en dosierformo DjVu
- Номидзу К. Группы Ли и дифференциальная геометрия. - Moskvo: eldonejo ИЛ, 1960, plena teksto en dosierformo DjVu
- Победря Б. Е. Лекции по тензорному анализу: Учеб. пособие. (3-е изд.). - Moskvo: eldonejo Изд-во МГУ, 1986;
- Рашевский П. К. Риманова геометрия и тензорный анализ (3-е издание). - Moskvo: eldonejo Наука, 1967;
Tensora programaro[redakti | redakti fonton]
- Cadabra - nefermita fontteksta komputila algebra sistemo kun subteno de tensoroj
- Tela - nefermita fontteksta programara pakaĵo dizajnita aparte por tensoroj.
- Maxima - libera nefermita fontteksta komputila algebra sistemo kiu povas esti uzata por tensoraj algebraj kalkuloj




































![{\displaystyle T_{[ij]}={1 \over 2}\left(T_{ij}-T_{ji}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32286060346007b0b5eef4e490360ce285b91171)

![{\displaystyle T_{[i_{1}\ldots i_{n}]}={1 \over n!}\sum _{\sigma }\mathrm {sign} (\sigma )T_{\sigma (i_{1})\ldots \sigma (i_{n})}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fece6b47af530a445490430b4b2efe349877bef0)










