Laterotranĉita 4-hiperkubo
| Laterotranĉita 4-hiperkubo | |
 Figuro de Schlegel centrita sur rombokub-okedro, okedraj ĉeloj estas montritaj | |
| Speco | Uniforma plurĉelo |
| Vertica figuro | Kvadrata kojno |
| Simbolo de Schläfli | t0,2{4,3,3} |
| Figuro de Coxeter-Dynkin | |
| Verticoj | 96 |
| Lateroj | 288 |
| Edroj | 128 trianguloj {3} 120 kvadratoj {4} |
| Ĉeloj | 8 malgrandaj rombokub-okedroj (3.4.4.4) 16 okedroj (3.3.3.3) 32 triangulaj prismoj (3.4.4) |
| Geometria simetria grupo | B4, [3,3,4] |
| Propraĵoj | Konveksa |
En geometrio, la laterotranĉita 4-hiperkubo estas uniforma plurĉeloj kun 56 ĉeloj: 8 malgrandaj rombokub-okedroj, 16 okedroj kaj 32 triangulaj prismoj.
Konstruado[redakti | redakti fonton]
En la procezo de laterotranĉo la edroj estas laterotranĉataj. La malgranda rombokub-okedro povas nomiĝi kiel laterotranĉita kubo, pro tio ke se ses edroj de kubo estas malpligrandigitaj en ilia respektivaj ebenoj, kaj la lateroj estas fortranĉitaj, rezultiĝas la malgranda rombokub-okedro. Ĉiu vertico apartiĝas en la tri novajn verticojn de la rombokub-okedraj trianguloj, kaj ĉiu latero apartiĝas en du novajn paralelajn laterojn inter kiuj aperas nova kvadrato.
Kiam la sama procezo estas aplikita al la 4-hiperkubo, ĉiu el la ok kuboj iĝas malgrandan rombokub-okedron en la priskribita maniero. Aldone tamen, pro tio ke ĉiu kuba latero estis antaŭe komunigita de tri kuboj, formiĝas tri paralelaj lateroj kiuj formas triangulan prismon, tiel aperas 32 triangulaj prismoj, ĉar komence estis 32 lateroj.
Plu, ĉar ĉiu vertico estis antaŭe komunigita de 4 kuboj, la vertico devus fendi en 12 novajn verticojn Tamen, pro tio ke la edroj de la fontaj kuboj daŭre estas komunigataj, en certaj 6 paroj el ĉi tiuj 12 potencialaj verticoj estas ili identaj unu al la alia, kaj pro tio nur 6 novaj verticoj estas kreitaj de ĉiu originala vertico (de ĉi tie la laterotranĉita 4-hiperkubo havas 96=16*6 verticojn). Ĉi tiuj ses novaj verticoj formas okedron, tiel aperas 16 okedroj, ĉar la fonta 4-hiperkubo havis 16 verticojn.
Strukturo[redakti | redakti fonton]
La 8 malgrandaj rombokub-okedroj estas kunigitaj unu la alian tra iliaj aksaj kvadrataj edroj. Iliaj ne-aksaj kvadrataj edroj, kiu respektivas al lateroj de la fontaj kuboj, estas koneksa al la triangulaj prismoj. La triangulaj edroj de la malgrandaj rombokub-okedroj kaj de la triangulaj prismoj estas koneksaj al la 16 okedroj.
Ĝia strukturo povas esti imagita per la 4-hiperkubo mem: la malgrandaj rombokub-okedroj estas analogaj al la 4-hiperkubaj ĉeloj, la triangulaj prismoj estas analogaj al la 4-hiperkubaj lateroj, kaj la okedroj estas analogaj al la 4-hiperkubaj verticoj.
Bildoj[redakti | redakti fonton]
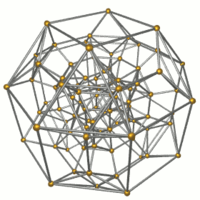
|
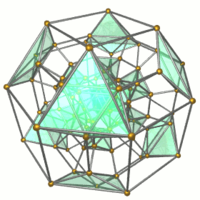
|

|
| Dratoframa | 16 okedroj montritaj | 32 triangulaj prismoj montritaj |
Projekcioj[redakti | redakti fonton]
Jen estas la aranĝo de la laterotranĉitaj 4-hiperkubaj ĉeloj sub la paralela projekcio en 3-dimensian spacon, malgranda rombokub-okedro estas la unua:
- La projekcia koverto estas senpintigita kubo.
- La plej proksima kaj la plej malproksima malgrandaj rombokub-okedroj projekciiĝas al volumenoj de la sama formo enskribitaj en la projekcian koverton.
- La aksaj kvadratoj de ĉi tiuj centraj malgrandaj rombokub-okedraj ektuŝmanieroj la centroj de la 6 oklateroj de la koverto. La oklateroj estas la bildo de la aliaj 6 malgrandaj rombokub-okedroj.
- La 12 kojno-similaj volumenoj konektanta la ne-aksaj kvadrataj edroj de la centra malgranda rombokub-okedro al la najbaraj oklateroj estas bildoj de 24 de la triangulaj prismoj.
- La ceteraj 8 triangulaj prismoj projekciiĝas sur la triangulajn edrojn de la koverto.
- Inter la triangulaj edroj de la koverto kaj la triangulaj edroj de la centra malgranda rombokub-okedro estas 8 okedroj, kiu estas la bildoj de la 16 okedraj ĉeloj.
Ĉi tiu aranĝo de ĉeloj en projekcio estas analoga al la aranĝo de edroj en la projekcio de la senpintigita kubo en 2 dimensiojn. De ĉi tie, la laterotranĉita 4-hiperkubo povas esti konsiderata kiel analogo de la senpintigita kubo en 4 dimensioj. (Ĝi estas ne la sola ebla analogo; alia proksima kandidato estas la senpintigita 4-hiperkubo.)
Alia uniforma plurĉelo kun simila aranĝo de ĉeloj estas la edroverticotranĉita 16-ĉelo.

