Kurbo de Bézier
En la matematika subkorpo de cifereca analitiko kurbo de Beziero (ang. Bézier curve) estas parametra kurbo grava en komputila grafiko. Ĝeneraligoj de Bézier kurboj al pli altaj dimensioj estas nomata kiel surfaco de Bézier (ang. Bézier surface).
Kurbo de Bézier estis larĝe publikigita en 1962 de la franca inĝeniero Pierre Bézier, kiu uzis ilin por desajni karoseriojn de aŭtoj. La kurboj estis unue ellaboritaj en 1959 de Paul de Casteljau per la algoritmo de Casteljau, kio estas ciferece stabila metodo al evaluado de kurboj de Bézier.
Linearaj kurboj de Bézier[redakti | redakti fonton]
Por donitaj punktoj P0 kaj P1, lineara Kurbo de Bézier estas rekta streko inter ĉi tiuj du punktoj. La kurbo estas donita per
Kvadrataj kurboj de Bézier[redakti | redakti fonton]
Kvadrata kurbo de Bézier estas la vojo spurata per la funkcio B(t), por donitaj punktoj P0, P1, kaj P2:
TTF-tiparoj uzas laŭpartajn interpolajn funkciojn de Bézier komponitajn el la kvadrataj kurboj de Bézier.
Kubaj kurboj de Bézier[redakti | redakti fonton]

Kvar punktoj P0, P1, P2 kaj P3 en la ebeno aŭ en tri-dimensia spaco difinas kuban kurbon de Bézier.
La kurbo startas je P0 irante direkte al P1 kaj alvenas je P3 devenante de la direkto de P2. Ĝenerale, ĝi ne trapasas tra P1 aŭ P2; ĉi tiuj punktoj estas nur por provizi direktojn. La distanco inter P0 kaj P1 difinas kiel longe la kurbo iras direkte al P1 antaŭ turno al P3.
La parametra formo de la kurbo estas:
Iuj bildo-prilaboraj sistemoj, inter ili PostSkripto kaj GIMP, uzas laŭpartajn interpolajn funkciojn de Bézier komponitajn el la kubaj kurboj de Bézier por desegnado de malrektaj linioj.
Kurboj de Bézier de ajna grado[redakti | redakti fonton]
La kurbo de Bézier de grado n povas esti donita sekve. Estu donitaj punktoj P0, P1,..., Pn. Tiam la kurbo de Bézier estas
kie estas binoma koeficiento
Ekzemple, por n=5:
La formulo povas esti skribita rikure per la samaj formuloj de grado n-1. Estu kurbo de Bézier de punktoj P0, P1,..., Pn. Tiam
Tiel, kurbo de Bézier de grado n estas lineara interpolo inter du kurboj de Bézier de grado n-1.
Notoj[redakti | redakti fonton]
Estu
la polinomoj
estas la bazaj polinomoj de Bernstein de grado n.
La punktoj Pi estas la apogaj punktoj por la kurbo. La plurlatero formita per trakonektanta la apogaj punktoj per rektaj strekoj, startante de P0 kaj finante kun Pn, kio estas, la konveksa koverto de la Pi , estas nomata kiel la plurlatero de Bézier, kaj la plurlatero de Bézier enhavas la kurbon de Bézier.
- La kurbo komenciĝas je P0 kaj finiĝas je Pn; ĉi tio estas tiel la fina punkta interpolo.
- La kurbo estas rekto se kaj nur se ĉiuj apogaj punktoj kuŝas sur la kurbo, simile, la kurbo estas rekto se kaj nur se la apogaj punktoj estas samrektaj.
- La starto kaj fino de la kurbo estas tanĝantaj respektive al la unua kaj lasta sekcioj de la plurlatero.
- La kurbo povas esti fendita je ĉiu punkto en 2 subkurbojn, aŭ en arbitre multajn subkurbojn, ankaŭ ĉiu el kiuj estas kurbo de Bézier.
- Nek cirklo nek arko de cirklo povas esti akurate prezentita kiel kurbo de Bézier. Tamen, n≥2 kubaj kurboj de Bézier povas proksimumigi cirklon. Por n=4, eblas atingi la radiusan eraron pli malgrandan ol 1/1000 de la radiuso.
- La kurbo je fiksita flanka orta ŝovo de donita kurbo de Bézier (simile kiel unu relo de fervoja trako relative al la alia) ne povas esti akurate prezentita kiel kurbo de Bézier en ĝenerala okazo. Tamen, eblas proksimumigaj manieroj kutime adekvataj por praktikaj celoj.
- Ĉiu kurbo de Bézier de grado n estas ankaŭ kurbo de Bézier de grado m por ĉiu m>n. Se estas kurbo de Bézier de grado n donita per punktoj P0, ..., Pn do ĝi estas ekvivalenta (eĉ je parametriogo) al la kurbo de grado n+1 donita per punktoj P'0, ..., P'n+1, kie .
Konstruado de kurboj de Bézier[redakti | redakti fonton]
Linearaj kurboj[redakti | redakti fonton]
La t en la funkcio por lineara kurbo de Bézier povas esti konsiderata kiel priskribanta kiel malproksime B(t) estas de P0 al P1. Ekzemple kiam t=0.25, B(t) estas je unu kvarono de la vojo de punkto P0 al P1. Kiam t varias de 0 al 1, B(t) priskribas rektan linion de P0 al P1.
Kvadrataj kurboj[redakti | redakti fonton]
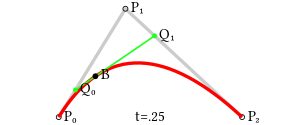
Por kvadrata kurboj de Bézier unu povas konstrui interajn punktojn Q0 kaj Q1 tiaj ke kiam t varias de 0 al 1:
- Punkto Q0 varias de P0 al P1 kaj priskribas linearan kurbon de Bézier.
- Punkto Q1 varias de P1 al P2 kaj priskribas linearan kurbon de Bézier.
- Punkto B(t) varias de Q0 al Q1 kaj priskribas kvadratan kurbon de Bézier.
Kubaj kurboj[redakti | redakti fonton]

Por kurboj de pli alta ordo oni bezonas respektive pli multajn interajn punktojn. Por kubaj kurboj oni povas konstrui interajn punktojn Q0, Q1 kaj Q2 kiuj priskribas linearajn kurbojn de Bézier, kaj punktojn R0 kaj R1 kiuj priskribas kvadratajn kurbojn de Bézier.
Kurboj de ordo 4[redakti | redakti fonton]

Por kvar-ordaj kurboj oni povas konstrui interajn punktojn Q0, Q1, Q2, Q3 kiuj priskribas linearajn kurbojn de Bézier; punktojn R0, R1, R2 kiuj priskribas kvadratajn kurbojn de Bézier; punktojn S0, S1 kiuj priskribas kubajn kurbojn de Bézier.
Animacioj[redakti | redakti fonton]
| Animacio de lineara kurbo de Bézier |
| Animacio de kvadrata kurbo de Bézier |
| Animacio de kuba kurbo de Bézier |
| Animacio de kurbo de Bézier de ordo 4 |
| Animacio de kurbo de Bézier de ordo 5 |
Uzoj en komputila grafiko[redakti | redakti fonton]
Kurboj de Bézier estas multe uzitaj en komputila grafiko kiel modelaj glataj kurboj. Pro tio ke la kurbo estas plene enhavata en la konveksa koverto de ĝiaj apogaj punktoj, la punktoj povas esti grafike elmontritaj kaj estas oportune manipuli la kurbon intuicie. Afinaj transformoj kiel movo, skaligo kaj turnado povas esti aplikitaj al la kurbo per aplikado al la ĉiuj apogaj punktoj de la kurbo.
La plej grava kurboj de Bézier estas kvadrataj kaj kubaj. Kurboj de la pli altaj gradaj estas pli multekostaj en komputado. Se pli komplikaj formoj estas bezonataj, la tuta kurbo estas disdividata je partoj, obeantaj certajn kondiĉoj je randoj por glateco. Ĉi tio estas tiel speco de laŭparta interpola funkcio - laŭparta interpola funkcio de Bézier.
Racionalaj kurboj de Bézier[redakti | redakti fonton]

Iuj kurboj kiuj aspektas kiel simpla, ekzemple cirklo, ne povas esti priskribitaj kiel kurbo de Bézier aŭ popeca kurbo de Bézier (kvankam en praktiko la diferenco estas malgranda kaj povas esti tolerebla). Por priskribi iujn el ĉi tiuj aliaj kurboj, oni bezonas aldonajn gradojn de libereco.
La racionala kurbo de Bézier aldonas pezojn kiuj povas esti ĝustigitaj. La numeratoro estas pezita kurbo de Bézier kaj la denominatoro estas pezita sumo de polinomoj de Bernstein.
Por donitaj n+1 apogaj punktoj Pi, la racionala kurbo de Bézier estas
kio estas
La racionala kurbo de Bézier povas precize prezenti konikojn.
Vidu ankaŭ[redakti | redakti fonton]
- Algoritmo de de Casteljau
- Laŭparta interpola funkcio
- Laŭparta interpola funkcio de Bézier
- B-laŭparta interpola funkcio
- Surfaco de Bézier
- Triangulo de Bézier
- Polinomo de Lagrange
Eksteraj ligiloj[redakti | redakti fonton]
- Paul Bourke: kurboj de Bézier, http://astronomy.swin.edu.au/~pbourke/curves/bezier/ Arkivigite je 2006-07-08 per la retarkivo Wayback Machine
- D-r Tomas Sederberg, BYU kurboj de Bézier, http://www.tsplines.com/resources/class_notes/Bezier_curves.pdf Arkivigite je 2006-02-21 per la retarkivo Wayback Machine
- Interaga apleto por kurboj de Bézier Arkivigite je 2007-10-10 per la retarkivo Wayback Machine
- Apleto por kurboj de Bézier de 3-a ordo
- Apleto
- Apletoj de malsamaj laŭpartaj interpolaj funkcioj
- Enkonduko al laŭpartaj interpolaj funkcioj
- Kuba laŭparta interpola funkcia biblioteko de Don Lancaster

![{\displaystyle \mathbf {B} (t)=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}{\mbox{ , }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0514431658e042fbb5523ea02d16d8afa0805272)
![{\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2t(1-t)\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/447ee28bb3a23751e3ae176ff85979c355f60419)
![{\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}(1-t)^{3}+3\mathbf {P} _{1}t(1-t)^{2}+3\mathbf {P} _{2}t^{2}(1-t)+\mathbf {P} _{3}t^{3}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/199d9916a0917ad0ae914189806693611c585a5b)
![{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}{n \choose i}\mathbf {P} _{i}(1-t)^{n-i}t^{i}=\mathbf {P} _{0}(1-t)^{n}+{n \choose 1}\mathbf {P} _{1}(1-t)^{n-1}t+\cdots +\mathbf {P} _{n}t^{n}{\mbox{ , }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bcef9b5ae096e7be85113e629064e01f2ad4a96)


![{\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}(1-t)^{5}+5\mathbf {P} _{1}t(1-t)^{4}+10\mathbf {P} _{2}t^{2}(1-t)^{3}+10\mathbf {P} _{3}t^{3}(1-t)^{2}+5\mathbf {P} _{4}t^{4}(1-t)+\mathbf {P} _{5}t^{5}{\mbox{ , }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce67646669e7dd2708aa76e9c0fd7a43f26876c8)


![{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}\mathbf {P} _{i}\mathbf {b} _{i,n}(t),\quad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6809080971ffd74cb48dbdc5b07c42575c7938a1)



