Romba dekduedro

Romba dekduedro
Klaku por rigardi turnantan bildon
Speco	Katalana solido Latero-transitiva, zonopluredro
Edra figuro	V3.4.3.4
Verticoj	14
Lateroj	24
Edroj	12
χ	2
Geometria simetria grupo	Oh
Duedra angulo	120°
Duala	Kubokedro
Bildo de duala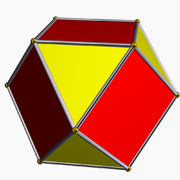

En geometrio, la romba dekduedro estas konveksa pluredro, katalana solido kun 12 rombaj edroj. Ĝia duala estas la kubokedro. Ĉar ĝi estas katalana solido do ĝi estas edro-transitiva kun malregulaj edraj plurlateroj.

Propraĵoj

Ĝi estas zonopluredro. La longa diagonalo de ĉiu edro estas akurate je √2 fojoj pli longa ol la mallonga diagonalo, do la anguloj de ĉiu edro estas cos⁻¹(1/3), aŭ proksimume 70,53°.

La romba dekduedro estas unu el la naŭ latero-transitivaj konveksaj pluredroj, ili estas 5 platonaj solidoj, kubokedro, dudek-dekduedro, romba dekduedro kaj romba tridekedro.

Parto de romba dekduedra kahelaro

La romba dekduedro povas esti uzata por kaheli 3-dimensian spacon. Iel simile al tio el seslateroj estas konstruita ebena seslatera kahelaro kaj el 24-ĉeloj estas konstruita 4-dimensia 24-ĉela kahelaro.

Ĉi tiu kahelaro estas la kahelaro de Voronoi de la kristalsistema edro-centrita kuba krado. Iuj mineraloj, ekzemple grenato formas romban dekduedran kristalan rutinon.

La romba dekduedro estas la vertico-centrita projekcio de 4-hiperkubo al 3 dimensioj. Estas ĝuste du vojoj de malkomponigo de romba dekduedro en 4 kongruajn paralelepipedojn, kune tiel estas 8 paralelepipedoj. La 8 ĉeloj de la 4-hiperkubo projekcias precize al ĉi tiuj 8 paralelepipedoj.

Areo kaj volumeno

La areo A kaj la volumeno V de la romba dekduedro de latera longo a estas:

$A=8{\sqrt {2}}a^{2}\approx 11.3137085a^{2}$

$V={\frac {16}{9}}{\sqrt {3}}a^{3}\approx 3.07920144a^{3}$

Karteziaj koordinatoj

Karteziaj koordinatoj de la ok verticoj kie tri edroj kuniĝas je iliaj malakutaj anguloj estas

(±1, ±1, ±1)

La koordinatoj de ses verticoj kie kvar edroj kuniĝas je iliaj akuta anguloj estas ĉiuj permutoj de

(0, 0, ±2)

Vidu ankaŭ

• Romba tridekedro
• Senpintigita romba dekduedro
• 24-ĉelo - kvar-dimensia analogo de la romba dekduedro

Referencoj

• Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)

Eksteraj ligiloj

• Eric W. Weisstein, Romba dekduedro en MathWorld.
• Virtualaj realaj pluredroj - la enciklopedio de pluredroj
• Romba Dekduedra Kalendaro – fari romba dekduedra kalendaro sen glui