Seria kaj paralela cirkvitoj
En elektrotekniko kaj elektroniko, komponantoj de elektronika cirkvito povas esti koneksaj serie aŭ paralele. Komponantoj koneksaj serie estas koneksaj laŭ sola vojo, tiel la sama kurento fluas tra ĉiuj komponantoj. Komponantoj koneksaj paralele estas koneksaj tiel ke la sama tensio estas aplikita al ĉiuj komponantoj.
Cirkvito komponita nur el komponantoj koneksaj serie estas seria cirkvito. Cirkvito komponita nur el komponantoj koneksaj paralele estas paralela cirkvito.
En seria cirkvito elektra tensio trans la cirkvito estas sumo de elektraj tensioj trans ĉiuj komponantoj. En paralela cirkvito la tuteca kurento estas sumo de kurentoj tra ĉiuj komponantoj.
Seriaj cirkvitoj[redakti | redakti fonton]
Rezistiloj[redakti | redakti fonton]
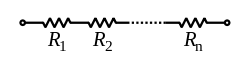 Serie koneksaj rezistiloj |
La tuteca rezistanco de serie koneksaj rezistiloj egalas al sumo de iliaj apartaj rezistancoj:
Kondensatoroj[redakti | redakti fonton]
 Serie koneksaj kondensatoroj |
La tuteca kapacitanco de serie koneksaj kondensatoroj egalas al inverso de sumo de inversoj de iliaj apartaj kapacitancoj:
En la plej bona okazo, la permesata maksimuma elektra tensio de seria kombinaĵo de kondensatoroj egalas al sumo de la permesataj elektraj tensioj de la apartaj kondensatoroj. Ĉi tiu la plej bona okazo rezultas se la permesataj elektraj tensioj de la apartaj kondensatoroj estas inverse proporciaj al iliaj kapacitancoj; ĝi estas en la plej kutima okazo de identaj kondensatoroj. Tamen, pro ebleco de ekzisto de nesciataj forfluaj kurenoj, ofte aldonaj paralelaj rezistiloj estas inde uzataj por certiĝi je egala disdivido de elektra tensio.
Induktiloj[redakti | redakti fonton]
 Serie koneksaj induktiloj |
La tuteca induktanco de serie koneksaj ne-kuplitaj induktiloj egalas al sumo de iliaj apartaj induktancoj:
Tamen, ofte estas malfacile malebligi magnetan interinfluon de najbaraj bobenoj, ĉar parto de magneta kampo de unu el ili trapasas tra la aliaj. Ĉi tiu influo estas priskribata per la reciprokaj induktancoj. La reciproka induktanco estas inter ĉiu duo de induktiloj. La tuteca kombinita induktanco estas egalas al sumo de ĉiuj reciprokaj induktancoj inter la diversaj induktiloj inkluzivante la reciprokajn induktancojn de ĉiu induktilo kun si.
kie n estas kvanto de la induktiloj,
- Mij estas reciproka induktanco de i-a al j-a induktilo.
Per reciprokeco estas Mij = Mji. Reciproka induktanco de induktilo kun si estas la sin-induktanco aŭ simple ĝia induktanco Li = Mii.
Tiel, se aparte skribi sin-induktancojn kaj kombini la samajn reciprokajn induktancojn
Ekzemple por tri induktiloj, estas ses reciprokaj induktancoj , , kaj , kaj . Estas ankaŭ la tri sin-induktancoj de la tri induktiloj: , kaj .
Pro tio
La lastaj du grupoj estas egalaj. La tri eroj de la unua grupo estas sin-induktancoj de la induktiloj. Tiel:
Por du induktiloj estas la sola reciproka induktanco M kaj
- L = L1+L2+2M
Noto ke signumoj de la reciprokaj induktancoj dependas de interŝanĝoj de bornoj de la induktiloj.
Ĉi tiu maniero povas esti uzata por kalkuli sin-induktancon de induktila bobeno granda aŭ de geometrie malsimpla formo, per konsiderado de ĝi kiel pluraj serie koneksaj simplaj malgrandaj induktiloj.
Impedancoj[redakti | redakti fonton]
Entuta impedanco de serie koneksaj cirkvitoj estas (se ne estas induktila kupliĝo inter la malsamaj cirkvitoj)
Ŝaltiloj[redakti | redakti fonton]
Kelkaj serie koneksaj ŝaltiloj faras funkcion logika KAJ. La tuta cirkvito estas ŝaltita se kaj nur se ĉiu el la ŝaltiloj estas ŝaltita.
Paralelaj cirkvitoj[redakti | redakti fonton]
Rezistiloj[redakti | redakti fonton]
 Paralele koneksaj rezistiloj |
La tuteca rezistanco de paralele koneksaj rezistiloj egalas al inverso de sumo de inversoj de iliaj apartaj rezistancoj:
Ĉi tio estas iam skribata kiel
La elektra kurento estas disdividata inter la komponantoj inverse proporcie al iliaj rezistancoj:
Kondensatoroj[redakti | redakti fonton]
 Paralele koneksaj kondensatoroj |
La tuteca kapacitanco de paralele koneksaj kondensatoroj egalas al sumo de iliaj apartaj kapacitancoj:
- .
La permesata maksimuma elektra tensio de paralela kombinaĵo de kondensatoroj estas limigita per la plej malgranda el la permesataj elektraj tensioj de la apartaj kondensatoroj.
Induktiloj[redakti | redakti fonton]
La tuteca induktanco de paralele koneksaj ne-kuplitaj induktiloj egalas al inverso de sumo de inversoj de iliaj apartaj induktancoj:
 Paralele koneksaj induktiloj |
Se la reciproka induktanco inter du induktiloj estas M, la ekvivalento induktanco estas
Se
Impedancoj[redakti | redakti fonton]
Entuta impedanco de paralele koneksaj cirkvitoj estas (se ne estas induktila kupliĝo inter la malsamaj cirkvitoj)
Ĉi tio estas iam skribata kiel
Ŝaltiloj[redakti | redakti fonton]
Kelkaj paralele koneksaj ŝaltiloj faras funkcion logika AŬ. La tuta cirkvito estas ŝaltita se kaj nur se almenaŭ unu el la ŝaltiloj estas ŝaltita.
Esperindeco[redakti | redakti fonton]
Komparo de esperindecoj de seria kaj paralela cirkvitoj dependas de tio kiel la komponantoj emas malfunkciiĝi.
Se domina maniero de malfunkciiĝo de ĉiu aparta komponanto estas distiriĝo do seria cirkvito estas malpli esperinda, ĉar distiriĝo de unu komponanto implicas ĉeson de funkciado de ĉiu komponantoj. En paralela cirkvito en okazo de distiriĝo de unu komponanto la aliaj komponantoj daŭre funkcias. Komuna ekzemplo estas elektraj lampoj; oni ilin kutime konektas paralele kaj se unu lampo forbruliĝas kaj distiriĝas la aliaj daŭre lumas.
Se domina maniero de malfunkciiĝo de ĉiu aparta komponanto estas mallonga cirkvito do paralela cirkvito estas malpli esperinda, ĉar mallonga cirkvito en unu komponanto implicas mallongan cirkviton ĉe la tuta cirkvito kaj ĉeson de funkciado de ĉiu komponantoj. En seria cirkvito en okazo de mallonga cirkvito en unu komponanto la aliaj komponantoj daŭre funkcias, kvankam tiam je ĉiu el la restantaj komponantaj estas pli granda tensio, kaj pro tiu probableco de malfunkciiĝo de ĉiu el ili pligrandiĝas. Pligrandigo de esperindeco de la tuta cirkvito per seria konektado estas iam uzata en grandtensiaj elektronikaj aparatoj; tiam apartaj komponantaj kaj ilia kvanto estas elektataj tiel ke eĉ en okazo de mallonga cirkvito en iu unu aŭ kelkaj komponantoj elektra tensio je la restantaj estas ne tro granda.
Plua pligrandigo de esperindeco de la tuta cirkvito povas esti farita per paralelo-seria konektado de pluraj komponantoj.
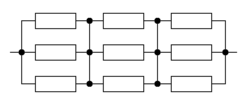  Variantoj de paralelo-seria konektado |
Malfunkciiĝo de ĉiu aparta komponanto estas distiriĝo pli ofta en praktiko kaj ofte estas konsiderata kiel defaŭlta. Ĉi tio gvidis al maniero de desegnado de kvazaŭ-cirkvitoj en teorio de esperindeco, kie paralelaj ero estas konsiderataj kiel rezervantaj unu la alian iu ajn sola funkcianta ero estas sufiĉa; kaj seriaj eroj estas konsiderataj kiel ke ili ĉiuj estas bezonataj por funkciado.
Vidu ankaŭ[redakti | redakti fonton]
Eksteraj ligiloj[redakti | redakti fonton]
- Kalkuliloj por rezistiloj en serie kaj paralele Arkivigite je 2013-05-04 per la retarkivo Wayback Machine
- Kio estas serio-paralela cirkvito
- Bildoj por seriaj paralelaj cirkvitoj[rompita ligilo]
- Virtuala eksperimento pri elektraj cirkvitoj



























