1 − 2 + 3 − 4 + · · ·

La unuaj miloj da terminoj kaj partaj sumoj de 1 − 2 + 3 − 4 + · · ·.

En matematikoj, la esprimo 1 − 2 + 3 − 4 + · · · estas senfina serio kies terminoj estas la pozitivaj entjeraj numeroj, tio estas naturaj numeroj, kiu ĝi alternas siajn signojn. Uzante matematikan notacion por sumatorias, la sumo de la unua m terminoj de la serio esprimas sin kiel:

$\sum _{n=1}^{m}n(-1)^{n-1}$

Estas diverĝa serio, en la senco ke la gamo de ĝiaj partaj sumoj (1, −1, 2, −2, …) ne inklinas neniun limon finito. En ekvivalenta formo oni diras ke 1 − 2 + 3 − 4 + · · · ne posedas sumon.

Tamen, meze de la 18a jarcento, Leonhard Eŭlero malkovras la sekvan rilaton kvalifikante ĝin de paradoksa:

$1-2+3-4+\cdots ={\frac {1}{4}}$

Ne estos ĝis multa tempo poste kiu oni sukcesas sin doni kun strikta ekspliko de la rilato. Al komencoj de la jardeko de 1890, Ernesto Cesàro kaj Émile Borel inter aliaj, ili enketis metodojn bone difinitaj por trovi sumojn ĝeneraligitajn de la diverĝaj serioj – inkludante novajn interpretojn de la provoj realigitaj de Eŭlero. Multaj de ĉi tiuj metodoj nomitaj sumacion atribuas al (1 − 2 + 3 − 4 + · · ·) "sumo" de 1⁄4. La metodo de sumo de Cesàro estas unu el la malmultaj metodoj kiujn ne adicias la serio 1 − 2 + 3 − 4 + · · ·, tial ĉi tiu serio estas ekzemplo de kazo kie oni devas uzi pli fortikan metodon kiel ekzemple la metodo de sumo de abel.

La serio 1 − 2 + 3 − 4 + · · · situas rilatigita kun la serio de Grandi 1 − 1 + 1 − 1 + · · ·. Eŭlero analizis ĉi tiujn du seriojn kiel specialajn kazojn de (1 − 2n + 3n − 4n + · · ·) por arbitraj valoroj de n, linio de esploro kiu etendas sian kontribuon al la problemo de Basilea kaj stiras al la funkciaj ekvacioj de kion ni konas hodiaŭ kiel la funkcio eta de Dirichlet kaj la funkcio zo de Riemann.

Diverĝo

La terminoj de la gamo, (1, −2, 3, −4, …), oni ne proksimiĝas al la 0; sekve la serio 1 − 2 + 3 − 4 + · · · diverĝas laŭ la testo de la termino. Kiel bazo de la analizo en sekcioj subsekvontoj, estas utila analizi la diverĝon en pli fundamenta nivelo. Por difino, la konverĝo aŭ diverĝo de senfina serio determinas sin analizante la konverĝon aŭ diverĝon de la gamo de siaj partaj sumoj, kaj en ĉi tiu kazo la partaj sumoj de 1 − 2 + 3 − 4 + · · · estas:

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

…

$\sum _{n=1}^{m}(-1)^{n-1}n\;\;={\frac {(-1)^{m-1}(2m+1)+1}{4}}$

Ĉi tiu gamo elstaras por enhavi fojon al ĉiu de la entjaj numeroj —ankoraŭ al la nulo se oni rakontas la malplenan partan sumon— kaj sekve ĝi establas la numerabilidad de la aro de la entjeroj.$\mathbb {Z}$ Klare ne proksimiĝas nek konverĝas al neniu numero aparte, sekve 1 − 2 + 3 − 4 + · · · diverĝas.

Rilatoj heŭristikaj de sumo

La plej simplaj eksplikoj kiuj rilatigas 1 − 2 + 3 − 4 + · · · kun la valoro 1⁄4 estas etendoj de rezultoj rilatigitaj kun la serio 1 − 1 + 1 − 1 + · · ·.

Stabileco kaj lineeco

Pro tio ke la terminoj (1, −2, 3, −4, 5, −6…) sekvas simplan mastron, oni povas esprimi al la serio 1 − 2 + 3 − 4 + · · · kiel versio transformita de si sama kaj solvi la rezultan ekvacion por akiri nombran valoron. Supozante ke estis ĝuste esprimi s = 1 − 2 + 3 − 4 + · · · por iu numero s, la sekvaj rilatoj stiras montri ke s = 1⁄4:

Adiciante 4 kopiojn de 1 − 2 + 3 − 4 + · · ·, uzante nur movojn kaj adiciante terminon al termino akiras sin 1.

s	= 1 − 2 + 3 − 4 + · · ·
= (1 − 1 + 1 − 1 + · · · ) + (0 − 1 + 2 − 3 + · · · )
= H − s,

Kie h estas la "sumo" de la serio:

H	= 1 − 1 + 1 − 1 + · · ·
= 1 − (1 − 1 + 1 − · · · )
= 1 − h.

Solvante la ekvaciojn h = 1 − h kaj s = h − s akiras sin ke h = 1⁄2 kaj s = 1⁄4.

En ekvivalenta formo, oni povas reordigi la ekvaciojn de formo tia de akiri (s + s) + (s + s) = h + h = 1, kiu denove implicas ke s = 1⁄4; estante ĉi tiu la formo kiu montriĝas en la skemo dekstre kaj en la esprimo tuj poste.

    s = 1 - 2 + 3 - 4 + 5 - 6 + . . . . . 
    s =   + 1 - 2 + 3 - 4 + 5 - . . . . . 
    s =   + 1 - 2 + 3 - 4 + 5 - . . . . . . 
    s =       + 1 - 2 + 3 - 4 + . . . . . . . 
--------------------------------------------
  4 s = 1 + 0 + 0 + 0 + 0 + 0 + . . . 

Kvankam la serio 1 − 2 + 3 − 4 + · · · ne posedas sumon en la kutima senco, la ekvacio s = ¹ − 2 + 3 − ₄ + · · · = 1⁄4 povas esti interpretita kiel la plej natura solvo en la kazo ke ĝi estis difinonta sin la valoro de koncerna sumo.

Difino ĝeneraligita de "sumo" de diverĝa serio estas nomita metodo de sumación; ekzistas pluraj malsamaj tipoj de metodoj, iuj de kiuj oni klarigas en la sekvaj sekcioj, kiuj karakteriziĝas por la proprietoj kiuj dividas kun la konvencia sumo.

La manipuladoj montritaj antaŭe pruvas ke: donita metodo de sumación kiu estas linia kaj stabila, se la sama sumo al la serio 1 − 2+ 3 − 4 + · · · tiam la sumo devas esti ¹⁄4, kaj tiu metodo ankaŭ permesos adicii al la serio de Grandi 1 − 1 + 1 − 1 + · · · ĵetante la valoron 1⁄2.

Al pezi ke la enfokusigo klarigita en la antaŭa alineo limigas la valorojn kiuj povas preni la sumojn ĝeneraligitajn de 1 − 2 + 3 − 4 + · · ·, la sama ne indikas kiuj estas la metodoj kiuj permesos adicii aŭ ne la serio. En efekto, iuj metodoj de sumación liniaj kaj stabilaj, tiaj kiaj la ordinara sumo, ili ne adicias al la serio 1 − 2 + 3 − 4 + · · ·. Se kontraŭe, ĝi esprimas sin la serio en alternativa formo kiel produkto, ĝi tiam eblas determini kiuj estas la metodoj kiuj permesas akiri 1⁄4.

Produkto de Cauchy

Jam en 1891, Ernesto Cesàro pensis ke la diverĝaj serioj estus korpigitaj en la estonteco al la matematika kalkulo de strikta maniero, indikante ke, "Hodiaŭ jam eblas skribi la esprimojn (1 − 1 + 1 − 1 + · · ·)² = 1 − 2 + 3 − 4 + · · · kaj aserti ke ambaŭ flankoj de la egaleco posedas la valoron 1/4." Por Cesàro, ĉi tiu ekvacio estis la rezulto apliki teoremon kiun li estis eldoninta dum la antaŭa jaro, estante dirita teoremo la unua en la historio de la diverĝaj serioj sumables. La detaloj de lia metodo de sumación oni klarigas en sekcioj subsiguientes; la centra ideo estas ke 1 − 2 + 3 − 4 + · · · estas la produkto de Cauchy de 1 − 1 + 1 − 1 + · · · kun 1 − 1 + 1 − 1 + · · ·.

La produkto de Cauchy de du senfinaj serioj difinas sin ankoraŭ se ambaŭ estas diverĝaj. En la kazo ke Σan = Σbn = Σ(−1)n, la terminoj de la produkto de Cauchy akiras sin per la sumo de la sumoj finitas de la diagonaloj:

${\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}$

Sekve la serio produkto rezultas esti:

$\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .$

Sekve la metodoj de sumación kiu "respektas" la produkto de Cauchy de du serioj kaj adicias 1 − ¹ + 1 − 1 + · · · = ¹⁄₂, ili ankaŭ adicias 1 − 2 + 3 − ₄ + · · · = 1⁄4.

Kaj en akordo kun la rezultoj de la antaŭa sekcio, ĉi tio implicas duoblan implicon inter la sumabilidad de 1 − 1 + 1 − 1 + · · · kaj 1 − 2 + 3 − 4 + · · · , por metodoj kiuj estas liniaj, stabilaj, kaj respektas la produkton de Cauchy.

La teoremo de Cesàro estas subtila ekzemplo. La serio 1 − 1 + 1 − 1 + · · · estas sumable Cesàro en malforta senco, identigita kiel sumable (C, 1), dum 1 − 2 + 3 − 4 + · · · postulas la uzon de pli potenca formo de la teoremo de Cesàro >, estante sumable (C, 2). Pro tio ke ĉiuj formoj de la teoremo de Cesàro estas liniaj kaj stabilaj, la sumoj rezultas en la valoroj indikitaj antaŭe.

Specifaj metodoj

Cesàro kaj Hölder

Esprimo de la sumo (H, 2) de 1/4.

Por kalkuli la sumación de Cesàro (C, 1) de 1 − 2 + 3 − 4 + · · ·, en la kazo ke ekzistis, oni devas kalkuli la aritmetikan mezumon de la partaj sumoj de la terminoj de la serio. La partaj sumoj estas:

1, −1, 2, −2, 3, −3, …,

Kaj la aritmetikaj mezumoj de ĉi tiuj partaj sumoj rezultas esti:

1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, ….

Pro tio ke ĉi tiu gamo ne konverĝas, ĝi tiam finas sin ke 1 − 2 + 3 − 4 + · · · ne estas sumable laŭ la metodo de Cesàro.

Ekzistas du ĝeneraliĝoj de la metodo de sumación de Cesàro: la plej simpla koncepte de la du estas la gamo de la metodoj (H, n) por naturaj numeroj n. La sumo (H, 1) estas la sumación de Cesàro, kaj la metodoj de pli granda ordono ripetas la kalkulon de la mezumoj. En la antaŭa esprimo, la mezumoj paroj konverĝas al 1⁄2, dum la neparaj mezumoj estas egalaj al nulo, sekve la mezumo de la mezumoj konverĝas al la valoro mezumon de 0 kaj 1⁄2, tio estas 1⁄4. Sekve 1 − 2 + 3 − 4 + · · · estas sumable (H, 2) ĵetante la valoron de 1⁄4.

La "H" oni uzas en honoro al Otto Hölder, kiu estis la unua en pruvi en 1882 kio hodiaŭ la matematikaj pensas estas la rilato inter la sumación abela kaj la sumación (H, n); sia unua ekzemplo estis 1 − 2 + 3 − 4 + · · ·. La fakto kiu ¹⁄₄ estas la sumo (H, 2) de 1 − 2 + 3 − 4 + · · · certigas ke estas ankaŭ la abela sumo; kio pruvas sin en la sekva sekcio.

La alia konata ĝeneraliĝo de la sumación de Cesàro estas la gamo de la metodoj (C, n). Pruvis sin ke la sumación (C, n) kaj la sumación (H, n) ĉiam donas la samajn rezultojn, kvankam ili havas malsamajn historiojn. En ¹887, Cesàro estis tre proksime de disvolvi la difinon de la sumación (C, n), sed nur donis malmultajn ekzemplojn, inkludante 1 − 2 + 3 − ₄ + · · ·, kiu adiciis akirante la valoron 1⁄4 por metodo kiu povus esti interpretita kiel (C, n) sed kiu ne estis pravigita kiel tia en tiu momento. Ĵus en 1890 Cesàro difinis formale al la metodoj (C, n) en la pruvo de sia teoremo, kiu diras ke la produkto de Cauchy de serio sumable (C, n) kaj serio sumable (C, m) estas serio sumable (C, m + n + 1).

Sumación abela

Iuj partaj de 1−2x+3x2+···; 1/(1 + x)2; kaj limoj en 1.

Leonhard Eŭlero en laboro kiu skribas al 1749 akceptas ke la serio diverĝas, sed de ĉiuj formoj faras la aprontes por adicii ŝin:

En pluraj ŝancoj Eŭlero proponis ĝeneraliĝon de la vorto "sumo". Liaj ideoj por la kazo de 1 − 2 + 3 − 4 + · · ·, estas similaj al kio hodiaŭ oni konas kiel Sumación de abel:

Ekzistas pluraj formoj kontroli ke, almenaŭ por absolutaj valoroj |x| < 1, Eŭlero estas en tio ĝusta asertinte ke:

$1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.$

Ekzemple se okazas disvolviĝo de Taylor de la dekstra flanko de la egaleco, aŭ oni aplikas la formalismon de Polinoma divido. Komencante de la maldekstra flanko, oni povas sekvi la heurística ĝenerala indikita antaŭe kaj provi multipliki por (1+x) du fojoj aŭ levi al la kvadrato la geometrian serion 1 − x + x2 − · · ·. Ŝajnus ke Eŭlero sugestas kalkuli la derivaĵon de ĉi tiu lasta serio termino al termino.

De moderna vidpunkto, la serio 1 − 2x + 3x2 − 4x3 + · · · ne difinas funkcion en x = 1, sekve koncerna valoro ne povas esti anstataŭita en la rezulta esprimo. Pro tio ke la funkcio estas difinita de ĉiu |x| < 1, sekve ĝi eblas kalkuli la limon kiam x inklinas 1, kaj ĉi tiu estas ĝuste la difino de la abela sumo:

$\lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.$

Eŭlero kaj Borel

Sumación de Eŭlero al 1⁄2 − 1⁄4.

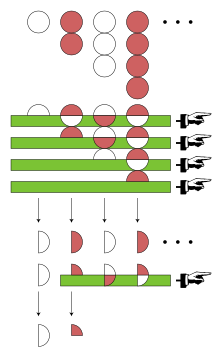
Eŭlero ankaŭ aplikis lin al la aliaj serioj tekniko de sia invento: la transformita de Eŭlero. Por kalkuli la transformitan de Eŭlero, ĝi komenciĝas por la gamo de pozitivaj terminoj kiuj formas la serion alternintan — en ĉi tiu kazo 1, 2, 3, 4, …. La unua elemento de ĉi tiu gamo nomiĝas a0.

Poste akiras sin la gamo de la antaŭaj diferencoj de 1, 2, 3, 4, …; kiu estas 1, 1, 1, 1, …. La unua elemento de ĉi tiu gamo nomas lin al li Δal0. La transformita de Eŭlero dependas ankaŭ de diferencoj de diferencoj, kaj iteraciones de pli granda ordono, sed ĉiuj antaŭaj diferencoj de 1, 1, 1, 1, … estas 0. La transformita de Eŭlero de 1 − 2 + 3 − 4 + · · · difinas sin kiel:

${\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.$

Uzante modernan terminologion, oni diras ke 1 − 2 + 3 − 4 + · · · estas sumable Eŭlero kun valoro 1⁄4.

La sumación de Eŭlero implicas ankaŭ alian tipon de sumación. Reprezentante 1 − 2 + 3 − 4 + · · · kiel:

$\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1),$

Akiras sin la plene konverĝa serio asociita:

$a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x).$

La sumo de Borel de 1 − 2 + 3 − 4 + · · · sekve estas

$\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}.$

Referencoj

• Beals, Richard (2004). Analysis: an introduction. Kembriĝo UP. ISBN 0-521-60047-2. 
• Davis, Harry F. (May de 1989). Fourier Serioj and Orthogonal Functions. Dover. ISBN 0-486-65973-9.  La referenco uzas malaktualajn parametrojn (helpo)
• Eŭlero, Leonhard; Lucas Willis; and Thomas J Osler (1768, 2006). «Translation with rimarkas of Eŭlero's paper: Vi rimarkas sudon beau rapport inter ilin séries donas puissances tant directes kiu réciproques». Memoires de l'academie donas sciences de Berlin 17: 83-106. 
• Ferraro, Giovanni (June de 1999). «The First Modern Definition of the Sum of al Divergent Serioj: An Aspect of the Rise of 20th Century Mathematics». Enarkivigas for History of Exact Sciences 54 (2): 101-135. Doi 10.1007/s004070050036.  La referenco uzas malaktualajn parametrojn (helpo)
• Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Eŭlero to Riemann. MIT Press. ISBN 0-262-07034-0. 
• Hardy, G.H. (1949). Divergent Serioj. Clarendon Press. 
• Kline, Morris (November de 1983). «Eŭlero and Infinite Serioj». Mathematics Magazine 56 (5): 307-314.  La referenco uzas malaktualajn parametrojn (helpo)
• Lavine, Shaughan (1994). Understanding the Infinite. Harvard UP. ISBN 0674920961. 
• Markushevich, Al.I. (1967). Serioj: fundamenta concepts with historical exposition (English translation of 3rd revised edition (1961) in Russian eldono). Hindustan Nokta trinkejo. Corp. 
• Saichev, Al.I., And W.Al. Woyczyński (1996). Distributions in the physical and engineering sciences, Volume 1. Birkhaüser. ISBN 0-8176-3924-1. 
• Tucciarone, John (January de 1973). «The development of the theory of summable divergent serioj from 1880 to 1925». Enarkivigas for History of Exact Sciences 10 (1-2): 1-40. Doi 10.1007/BF00343405.  La referenco uzas malaktualajn parametrojn (helpo)
• Vretblad, Anders (2003). Fourier Analysis and Its Applications. Springer. ISBN 0387008365. 
• Weidlich, John E. (June de 1950). Summability methods for divergent series. Stanford M.S. Theses. OCLC 38624384.  La referenco uzas malaktualajn parametrojn (helpo)