Leĝo de sinusoj
En trigonometrio, la leĝo de sinusoj aŭ sinusa formulo aŭ sinusa regulo aŭ sinusa teoremo estas interrilato inter longoj de lateroj kaj sinusoj de anguloj ĉe triangulo sur eŭklida ebeno.
Se longoj de lateroj de la triangulo estas a, b kaj c kaj la anguloj kontraŭaj al tiuj lateroj estas A, B kaj C, tiam la leĝo de sinusoj estas:
kie R estas la radiuso de la ĉirkaŭskribita cirklo.
Plu
kie S estas la areo de la triangulo kaj s estas la duonperimetro
La dua egaleco pli supre estas esence formulo de Heron.
La ambigua okazo[redakti | redakti fonton]

Kiam uzanta la leĝo de sinusoj estas uzata por solvi triangulon, sub specifaj kondiĉoj ekzistas ambigua okazo, kiam eblas du malsamaj solvaĵoj kaj du malsamaj trianguloj povas esti konstruitaj.
Donita ĝenerala triangulo ABC, ĉiuj jenaj kondiĉoj devas esti veraj por ke la okazo estu ambigua:
- La nura informo sciata pri la triangulo estas la angulo A kaj la lateroj a kaj b.
- La angulo A estas akuta (A<90°).
- La latero a estas pli mallonga ol latero b (a<b).
- La latero a estas pli longa ol la kateto de orta triangulo kun angulo A kaj hipotenuzo b (a > b sin A).
Tiam, la angulo B povas esti kaj akuta aŭ malakuta:
aŭ
Pruvo[redakti | redakti fonton]
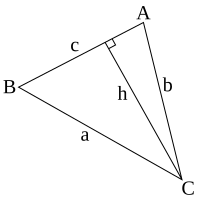
Estu triangulo kun la lateroj a, b, kaj c, kaj anguloj A, B, kaj C. Estu h longo de alto de angulo C al c. tiam:
Pro tio
kaj
Farante la samon kun alto inter angulo A kaj latero a oni ricevas na:
Leĝo de sinusoj por kvaredroj[redakti | redakti fonton]
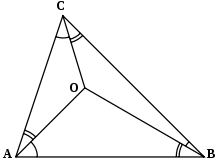
Estu kvaredro kun verticoj O, A, B, C. Tiam:
La du flankoj de ĉi tiu idento respektivas al laŭhorloĝnadla kaj kontraŭhorloĝnadla orientiĝoj de la surfaco.
Metante ĉiun el la kvar verticoj en la rolo de O oni ricevas kvar tiajn identojn, sed maksimume tri el ili estas sendependa: Se la laŭhorloĝnadlaj flankoj de tri el ili estas multiplikitaj kaj la produto estas konkludita al esti egala al la produto de la kontraŭhorloĝnadlaj flankoj de la samaj tri identoj, kaj tiam komunaj faktoroj estas forigitaj de ambaŭ flankoj, la rezulto estas la kvara idento. Unu kaŭzo al havi intereson al ĉi tiu sendependeco de rilatoj estas ĉi tiu: tri anguloj estas la anguloj de iu triangulo se kaj nur se ilia sumo estas duono-cirklo; kia kondiĉo sur 12 anguloj estas necesa kaj sufiĉa por ke ili estu la 12 anguloj de iu kvaredro? Klare la sumo anguloj de ĉiu edro de la kvaredro devas esti duono-cirklo. Pro tio ke estas kvar tiaj trianguloj, estas kvar tiaj limigoj sur sumoj de anguloj, kaj la kvanto de gradoj de libereco estas pro tio malpligrandigita de 12 al 8. La kvar rilatoj donitaj per ĉi tiu sinusaj leĝo plu malpligrandigas la kvanton de gradoj de libereco, sed ne de 8 suben ĝis 4, sed nur de 8 suben ĝis 5, pro tio ke la kvara limigo estas ne sendependa de la unuaj tri. Tial la spaco de ĉiuj formoj de kvaredroj estas 5-dimensia.
Vidu ankaŭ[redakti | redakti fonton]
Eksteraj ligiloj[redakti | redakti fonton]
- Areo kaj leĝo de sinusoj Arkivigite je 2008-04-18 per la retarkivo Wayback Machine je PlainMath
- Leĝo de sinusoj Arkivigite je 2008-05-16 per la retarkivo Wayback Machine
- Leĝo de sinusoj je tranĉi-la-nodon
- Grado de kurbeco
- Leĝo de sinusoj Arkivigite je 2008-04-18 per la retarkivo Wayback Machine je PlainMath
| ||||||||||











