Ĉirkaŭskribita cirklo

En geometrio, la ĉirkaŭskribita cirklo de plurlatero estas cirklo, kiu pasas tra ĉiuj verticoj de la plurlatero.
Plurlatero, kiu havas ĉirkaŭskribitan cirklon, estas cikla plurlatero. Ĉiu regula plurlatero, ĉiu triangulo kaj ĉiu ortangulo estas cikla.
Rilatanta nocio estas la minimuma baranta cirklo, kiu estas la plej malgranda cirklo kiu plene enhavas la plurlateron. Ne ĉiu plurlatero havas ĉirkaŭskribitan cirklon, ĉar verticoj de plurlatero ne nepre ĉiuj kuŝi sur cirklo. Sed ĉiu plurlatero havas unikan minimuman barantan cirklon, kiu povas esti konstruita per algoritmo dum lineara tempo. Eĉ se plurlatero havas ĉirkaŭskribitan cirklo, ĝi povas ne koincidi kun ĝia minimuma baranta cirklo; ekzemple, por malakuta triangulo, la minimuma baranta cirklo havas la plej longan lateron de la triangulo kiel diametro kaj ne trapasas la verticon kun angulo pli granda ol orto.
Ĉirkaŭskribita cirklo de triangulo[redakti | redakti fonton]

Ĉiu triangulo estas cikla, aŭ alivorte ĉiu triangulo havas ĉirkaŭskribitan cirklo.
La centro de ĉirkaŭskribita cirklo de triangulo povas troviĝi kiel la komunaĵo de la tri perpendikularoj al lateroj je iliaj mezpunktoj. Ĉi tiu punkto estas la centro de ĉirkaŭskribita cirklo ĉar ĝi estas samdistanca de la triangulo, do samdistanca de ĉiuj tri verticoj de la triangulo.
La situo de centro de ĉirkaŭskribita cirklo dependas sur la speco de triangulo:
- Se kaj nur se triangulo estas akuta (ĉiuj anguloj pli malgrandaj ol orto), la centro de ĉirkaŭskribita cirklo kuŝas en la triangulo.
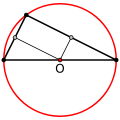
- Se kaj nur se ĝi estas orta triangulo, la centro de ĉirkaŭskribita cirklo kuŝas sur unu el ĝiaj lateroj, la hipotenuzo. Ĉi tio estas unu el formoj de teoremo de Taleso.
- Se kaj nur se ĝi estas malakuta (unu angulo estas pli granda ol orto), la centro de ĉirkaŭskribita cirklo kuŝas ekstere.
-
Centro de ĉirkaŭskribita cirklo de akuta triangulo estas en la triangulo
-
Centro de ĉirkaŭskribita cirklo de orta triangulo estas sur la hipotenuzo
-
Centro de ĉirkaŭskribita cirklo de malakuta triangulo estas ekster la triangulo
La diametro de la ĉirkaŭskribita cirklo povas estas egala al longo de iu latero de la triangulo dividita per sinuso de la kontraŭa angulo. La rezulto ne dependas de tio kiu latero estas konsiderata, pro la leĝo de sinusoj. La eŭlera cirklo de la triangulo havas diametron kiu estas duono de diametro de la ĉirkaŭskribita cirklo. Diametro d de la ĉirkaŭskribita cirklo de triangulo estas:
- kie a, b, c estas la longoj de la lateroj de la triangulo,
- kaj A, B, C estas la anguloj kontraŭaj al la respektivaj antaŭaj lateroj.
Alia formulado estas la sekva:
En ĉiu triangulo, la centro de ĉirkaŭskribita cirklo, la pezocentro kaj altocentro estas ĉiam sur la sama rekto kiu estas nomata kiel la eŭlera rekto.
La vertico-transitiva konjugita de la centro de ĉirkaŭskribita cirklo estas la altocentro.
Anguloj je kiuj lateroj intersekciĝas kun la cirklo[redakti | redakti fonton]


La anguloj je kiu la ĉirkaŭskribita cirklo intersekciĝas kun latero de la triangulo koincidas kun angulo je kiu du la aliaj lateroj sekcas unu la alian.
Ĉirkaŭskribita cirklo de kvarlatero[redakti | redakti fonton]

Kvarlatero, kiu povas esti ĉirkaŭskribita, havas apartajn proprecojn, inter ili estas tiu laŭ kiu la sumo de la kontraŭaj anguloj estas 180° aŭ π radianoj.
Vidu ankaŭ[redakti | redakti fonton]
- Ĉirkaŭskribita sfero
- Enskribita cirklo
- Eŭlera cirklo
- Teoremo de Jung, neegalaĵo kun la diametro de punkta aro kaj la radiuso de ĝia minimuma baranta cirklo
- Teoremo de Lester
- Teoremo de Carnot
- Mezortanto
Referencoj[redakti | redakti fonton]
- Megiddo, N (1983). “Linear-time algorithms for linear programming in R3 and related problems - Linearo-tempaj algoritmoj por lineara programado en R3 kaj rilatantaj problemoj”, SIAM Journal on Computing - SIAM ĵurnalo pri komputado 12, p. 759–776.
- Kimberling, Clark (1998). “Triangle centers and central triangles - Triangulaj centroj kaj centraj trianguloj”, Congressus Numerantium 129, p. i–xxv, 1–295.
- Daniel Pedoe. (1988) Geometry: a comprehensive course - Geometrio: multampleksa kurso. Dover.
Eksteraj ligiloj[redakti | redakti fonton]
- Triangulaj centroj
- Triangulo ĉirkaŭskribita cirklo kaj Centro de ĉirkaŭskribita cirklo kun interaga animacio
- Ĉirkaŭskribita cirklo je MathWorld
- Ĉirkaŭskribita elipso de Steiner je MathWorld
- Interaga Java apleto por centro de ĉirkaŭskribita cirklo Arkivigite je 2007-08-19 per la retarkivo Wayback Machine