Malalta-pasa filtrilo

Malalta-pasa filtrilo aŭ alta-tranĉa filtrilo estas filtrilo kiu trapasigas signalojn de malaltaj frekvencoj kaj malamplifas (malpligrandigas je amplitudo aŭ povumo) signalojn de pli altaj frekvencoj. La frekvenco proksime de kiu okazas la disdivido estas la fortranĉa frekvenco. La reala kvanto de malamplifo por ĉiu frekvenco varias de filtrilo al filtrilo. Malalta-pasa filtrilo estas kontraŭa de alta-pasa filtrilo, kaj bendo-pasa filtrilo estas kombinaĵo de malalta-pasa kaj alta-pasa filtriloj.
Malalta-pasaj filtriloj ekzistas en multaj malsamaj formoj, inkluzivante elektronikajn cirkvitojn, ciferecajn filtrilojn por glatigado de aroj de datumoj, akustikajn barilojn, malklarigon de bildoj, kaj tiel plu. La movanta averaĝa operacio uzata por prilaboro de tabeloj de nombraj datumoj estas speco de malalta-pasa filtrilo, kaj povas esti analizita kun la samaj signal-prilaboradaj manieroj kiuj estas uzataj por la alia malalta-pasaj filtriloj.
Malalta-pasaj filtriloj provizas glatigon de formo de signalo, forprenante la mallonge daŭrajn fluktuojn, kaj lasante la pli longe daŭrajn tendencojn.
La signifoj de vortoj "malalta" kaj "alta" en la nomo de la filtrilo estas nur la karakterizo de la filtrilo relative al si mem. La termino "malalta-pasa filtrilo" nur temas pri la formo de la filtrila frekvenca karakterizo; iu alta-pasa filtrilo povas esti konstruita tiel ke ĝi tranĉas for je pli suba frekvenco ol iu malalta-pasa filtrilo; la nomo ne difinas komparon de karakterizoj de pluraj filtriloj.
Ankaŭ integralilo estas ekzemplo de malalta-pasa filtrilo.
Ekzemploj de malalta-pasaj filtriloj[redakti | redakti fonton]
Optiko[redakti | redakti fonton]

Akustiko[redakti | redakti fonton]
Malmola fizika barilo pli multe reflektas pli altajn sonajn frekvencojn, kaj tiel agas kiel malalta-pasa filtrilo por elsendanta sono. Kiam muziko estas aŭdata el alia ĉambro, la malaltaj notoj estas pli facile aŭdataj, kaj la altaj notoj estas pli malamplifataj.
Elektroniko[redakti | redakti fonton]
Elektronikaj malalta-pasaj filtriloj estas uzataj por doni signalon al malalta-frekvencaj laŭtparoliloj, por bari altajn frekvencojn kiujn ili ne povas kompetente disaŭdigi.
Radiaj sendiloj uzas malalta-pasajn filtrilojn por malamplifi harmonajn eligojn kiuj povus kaŭzi perturbon kun la aliaj komunikaĵoj.
Telefonaj linioj kun DSL-fendigiloj uzas malalta-pasajn kaj alta-pasajn filtrilojn por apartigi DSL kaj telefonan signalojn trapasanajn la saman paron de dratoj.
Elektronikaj malalta-pasaj filtriloj estas uzataj por filtri elektran povumon, ĉar la povumo estas donata kutime per alterna kurento kun industria frekvenco (50 aŭ 60 hercoj) aŭ per kontinua kurento (plejparte ene de elektronikaj aparatoj), kaj perturbaj signaloj havas pli grandajn frekvencojn.
Ideala kaj reala filtriloj[redakti | redakti fonton]

Ideala malalta-pasa filtrilo (sinc-filtrilo) plene eliminas ĉiujn frekvencojn pli supre de la fortranĉa frekvenco trapasigante ĉiujn frekvencojn pli sube neŝanĝitajn. Ĝia frekvenca respondo estas ortangula funkcio, kaj ĝi tiel estas briko-mura filtrilo. La parte traira regiono havata de praktikaj filtriloj ne ekzistas en ideala filtrilo.
Impulsa respondo de ideala malalta-pasa filtrilo estas sinc-funkcio. Tiel ideala malalta-pasa filtrilo povas esti komprenita matematike (teorie) per multiplikado de signalo kun la ortangula funkcio en la frekvenca domajno aŭ, ekvivalente, per kunfaldado kun la sinc-funkcio en la tempa domajno.
Tamen, la ideala filtrilo estas neebla sen havo de signalo de malfinia amplekso en ĉiu tempo, ĉar ĉe la sinc funkcio subtena regiono (regiono en kiu ĝi estas ne nula) etendiĝas malfinien en ambaŭ pasintecon kaj estonton. La filtrilo de signalo ŝanĝanta kun tempo devus pro tio bezone havi malfinian malfruon, aŭ scion de la malfinia estonto kaj pasinteco, por ke plenumi la kunfaldaĵon. Ĉi tio estas efike realigebla por antaŭe plene skribitaj ciferecaj signaloj per alpreno de ĝia vastigaĵo kiel nulo en la pasintecon kaj estonton, aŭ per faro de la signalo al esti ripetanta (kaj tiam eblas uzi la analizon de Fourier).
Realaj filtriloj por realo-tempa funkciado aproksimas la idealan filtrilon per tranĉo kaj fenestrado de la malfinia impulsa respondo por fari tiel ke la impulsa respondo estu finia almenaŭ en estonton. Apliko de ĉi tia filtrilo postulas malfruigon de la signalo por modera tempodaŭro, permesante al la kalkulado vidi nur iom malmulte en la estonton. Ĉi tiu malfruo aspektas kiel faza ŝovo. Pli granda akurateco en proksimumado de la ideala filtrilo postulas pli longan malfruon.
Ideala malalta-pasa filtrilo rezultas je sonorantaj aperaĵoj tra la fenomeno de Gibbs. Ĉi tiuj povas esti malpligrandigitaj aŭ pligrandigitaj per elekto de fenestra funkcio, kaj la dizajno kaj elekto de realaj filtriloj engaĝas komprenon kaj minimumigon de ĉi tiuj aperaĵoj. Ekzemple, simpla tranĉo de sinc kaŭzas severajn sonorantajn aperaĵojn en signala rekonstruado, kaj por malpligrandigi la aperaĵojn oni uzas fenestrajn funkciojn kiuj malpligrandiĝas al nulo pli glate ĉe la randoj.
La interpola formulo de Whittaker-Shannon priskribas kiel uzi perfektan malalta-pasan filtrilon por rekonstrui kontinuan signalon surbaze de cifereca signalo konsistanta el apartaj specimenoj de la signalo je iuj diskretaj tempoj. Realaj cifereca-al-analogaj konvertiloj uzas realajn proksimumantajn filtrilojn.
Kontinua-tempaj malalta-pasaj filtriloj[redakti | redakti fonton]

Estas multaj malsamaj specoj de filtrilaj cirkvitoj, kun malsamaj respondoj al ŝanĝanta frekvenco. La frekvenca respondo de filtrilo estas ĝenerale prezentata per amplitudo-frekvenca karakterizo kaj fazo-frekvenca karakterizo (grafika prezento de Bode), kaj la filtrilo estas karakterizata per ĝia fortranĉa frekvenco kaj kurzo de pligrandiĝo de la malamplifo kun pligrandiĝo de la frekvenco. Je la fortranĉa frekvenco, la filtrilo malamplifas la enigan povumon dufoje, kio estas proksimume je 3 dB.
La ordo de la filtrilo difinas la kvanton de aldona malamplifo por frekvencoj pli altaj ol la fortranĉa frekvenco. Je sufiĉe altaj frekvencoj, pli ĝuste en la limeso kun frekvenco strebanta al malfinio, ĉe la filtrilo de ordo n, ne havanta nulojn de la tradona funkcio, plia malpligrandigo de la signalo estas je 20n dB kun dekobliĝo de frekvenco. Ĉi tio estas ke plia malpligrandigo de la amplitudo de la eliga signalo estas je 10n fojoj kun dekobliĝo de frekvenco aŭ ekvivalente ke plia malpligrandigo de la povumo de la eliga signalo estas je 100n fojoj kun dekobliĝo de frekvenco. Ĉi tio estas ke kun duobliĝo de frekvenco, kio estas trairo supren je unu okto, plia malpligrandigo de la signalo estas je 20(log10(2))n dB; ĉi tio estas proksimume je 6,0206n dB aŭ pli proksimume je 6n dB.
- Unua-ordo filtrilo, estas tiu ĉe kiu malpligrandigo de la signalo estas je 20 dB kun dekobliĝo de frekvenco. La grafika prezento de Bode por unua-orda filtrilo aspektas simile al horizontalo pli sube de la fortranĉa frekvenco, kaj simile al diagonala linio pli supre la fortranĉa frekvenco. Estas ankaŭ "genua kurbo" je la rando inter la du, kiu estas glata trairo inter la du rektaj regionoj. Se la tradona funkcio de unua-orda malalta-pasa filtrilo havas nulon kaj ankaŭ poluson, la grafika prezento de Bode horizontaliĝos denove je sufiĉe altaj frekvencoj, je iu maksimuma malamplifo; ĉi tia efiko povas esti kaŭzita ekzemple per iu malgranda liko de la eniga signalo ĉirkaŭ la unu-polusa filtrilo. Ĉi tiu unu-polusa-unu-nula filtrilo estas ankoraŭ unua-orda malalta-pasa filtrilo.
- Dua-orda filtrilo malamplifas pli altajn frekvencojn pli krute. La grafika prezento de Bode por ĉi tiu speco de filtrilo similas al tiu de unua-orda filtrilo, escepte de tio ke ĝi falas pli rapide. Ekzemple, dua-orda filtrilo de Butterworth malpligrandigas la signalan amplitudon al unu centono de ĝia originala nivelo, aŭ je 40 dB, ĉiufoje kiam la frekvenco dekobliĝas. La aliaj ne havantaj nulojn filtriloj povas havi malsamajn
kurzojn ĉirkaŭ la fortranĉa frekvenco dependante de ilia Q-faktoro, sed proksimiĝas al la sama fina kurzo de 40 dB por dekobilĝo de frekvenco. Same kiel ĉe la unua-ordaj filtriloj, nuloj de la tradona funkcio povas ŝanĝi la alta-frekvencan asimptoton.
La diversaj specoj de filtriloj, inter ili filtrilo de Butterworth, filtrilo de Ĉebiŝev, filtrilo de Bessel, havas malsame aspektantajn genuan kurbon. Ĉe ĉiu filtrilo de Butterworth, se etendi la horizontalon dekstren kaj la diagonala linio al la supro-maldekstro (la asimptotojn de la funkcio), ili intersekciĝas je akurate la fortranĉa frekvenco. Multaj filtriloj estas dizajnitaj por havi akraĵon aŭ resonancon, kaŭzantan ke ilia frekvenca respondo je la fortranĉa frekvenco estu pli supre de la horizontalo. La resonanco eblas por filtriloj de ordo du aŭ pli granda.
Laplaca skribmaniero[redakti | redakti fonton]
Kontinua-tempaj filtriloj povas ankaŭ esti priskribitaj per la laplaca konverto de ilia impulsa respondo. Ĉio tio permesas facile analizi ĉiujn karakterizojn de la filtrilo per konsidero de la polusoj kaj nuloj de la laplaca konverto en la kompleksa ebeno. En diskreta tempo, oni povas simile konsideri la Z-konverton de la impulsa respondo.
Ekzemple, unua-orda malalta-pasa filtrilo povas esti priskribita en laplaca skribmaniero kiel
kie s estas la laplaca konverta variablo, τ estas la filtrila tempa konstanto, kaj K estas la filtrila amplifo en la pasanta bendo.
Elektronikaj malalta-pasaj filtriloj[redakti | redakti fonton]
Pasiva RC-cirkvito[redakti | redakti fonton]

Simpla elektra cirkvito kiu servas kiel unua-orda malalta-pasa filtrilo konsistas de rezistilo en serio inter la fonto de la signalo kaj la eliro, kaj kondensatoro en paralelo kun la eliro. La kondensatoro eksponas reaktancon, kaj forbaras alta-frekvencajn signalojn, kaŭzante ke ili iras al la komuna drato tra la kondensatoro sed ne tra la ŝarĝo alkroĉita al la eliro. Je pli altaj frekvencoj la reaktanco falas, kaj la kondensatoro pli efike funkcias kiel barilo. La kombinaĵo de rezisto kaj kapacitanco donas la tempan konstanton de la filtrilo τ=RC' (prezentita per la greka litero taŭo). La fortranĉa frekvenco estas difinita per la tempa konstanto:
aŭ ekvivalente la frekvenco en radianoj por sekundo estas
La alia maniero kompreni funkciadon de ĉi tiu cirkvito estas per konsidero de la tempo kiun la kondensatoro bezonas por ŝargiĝi tra la rezistilo:
- Je malaltaj frekvencoj, estas multo da tempo por ke la kondensatoro ŝargiĝu ĝis praktike la sama elektra tensio kiel la eniga elektra tensio.
- Je altaj frekvencoj, la kondensatoro nur havas tempon por ŝargiĝi je malgranda kvanto antaŭ kiam la enigo reŝaltiĝas je la alia signumo. La eligo iras supren kaj suben nur je malgranda parto de la kvanto je kiu la enigo iras supren kaj suben. Je plia duobliĝo de la frekvenco, tie estos nur tempo por ke ĝi ŝargiĝu supren je proksimume duono de la kvanto je la fonta frekvenco.
Pasiva LR-cirkvito[redakti | redakti fonton]
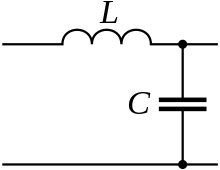
Simpla elektra cirkvito kiu servas kiel unua-orda malalta-pasa filtrilo konsistas de induktilo en serio inter la fonto de la signalo kaj la eliro, kaj rezistilo en paralelo kun la eliro.
La kombinaĵo de induktanco kaj rezisto donas la tempan konstanton de la filtrilo τ=L/R (prezentita per la greka litero taŭo). La fortranĉa frekvenco estas difinita per la tempa konstanto:
aŭ ekvivalente la frekvenco en radianoj por sekundo estas
Pasivaj cirkvitoj de pli altaj ordoj[redakti | redakti fonton]

Pasivaj elektronikaj cirkvitoj de pli grandaj ordoj povas esti konstruitaj per kombinigo de la pli supre priskribitaj cirkvitoj de la unua ordo.
Se amplifilo de amplifo 1 (bufro) estas metita inter la pasivaj filtriloj, do ili ne interagas kaj la amplitudo-frekvenca karakterizo de la tuto egalas al produto (sumo je logaritma skalo) de amplitudo-frekvencaj karakterizoj de la apartoj filtriloj. Se ilin kunigi sen bufro do okazas interago, kaj la rezulta amplitudo-frekvenca karakterizo tiam estas la alia je iu grado.
La pli ofte uzataj estas plurera RC filtrilo kaj LC filtrilo. Ĝenerale la ordo de la filtrilo estas ne pli granda ol la suma kvanto de L kaj C eroj en la cirkvito.
Aktivaj elektronikaj filtriloj[redakti | redakti fonton]

Aktiva malalta-pasa filtrilo de dua ordo
Alia speco de elektra cirkvito estas aktiva malalta-pasa filtrilo.
Por la cirkvito kun operacia amplifilo, montrita en la figuro, la fortranĉa frekvenco estas
aŭ ekvivalente en radianoj por sekundo:
La simple amplifanta amplifilo konsistanta al operacia amplifilo kaj du rezistiloj estas konvertita en malalta-pasan filtrilo per simpla aldono de retrokupla kondensatoro C. Ĉi tiu retrokuplo malaltigas la frekvencan respondon je altaj frekvencoj, kaj ankaŭ helpas eviti osciladon en la amplifilo.
La amplifo en la pasanta bendo estas -R2/R1, kaj je la altaj frekvencoj malamplifo kreskas je 20 dB kun dekobliĝo de frekvenco, kiel por unua-orda filtrilo. Tamen, la malamplifo tiel kreskas nur ĝis frekvencoj je kiuj la amplifilo konservas siajn kapablojn amplifi, ĉiu amplifilo havas limigitan frekvencan bendon de funkciado. Je pli altaj frekvencoj, la malamplifo povas eĉ malpligrandiĝi, ĉar la amplifilo povas ne funkcii kaj la signalo povas iri ĉirkaŭ ĝi tra la kondensatoro.
Diskreta-tempa kompreno[redakti | redakti fonton]
La efiko de malalta-pasa filtrilo povas esti simulita per komputilo per analizo de ĝia konduto en la tempa domajno, kaj por tio diskretigo de la modelo.
Laŭ la leĝo de Ohm kaj la difino de kapacitanco, eblas skribi ekvaciojn priskribantajn RC-filtrilon
- (1)
- (2)
- (3)
kie Qc(t) estas la ŝargo konservita en la kondensatoro je tempo t;
- venen(t) estas la eniga signalo je tempo t;
- vel(t) estas la elira signalo je tempo t;
- i(t) estas la elektra kurento tra la rezitilo kaj la kondensatoro je tempo t.
Anstataŭo de ekvacio (2) en ekvacion (3) donas
kiu povas esti anstataŭita en ekvacion (1) kaj kun tio ke τ=RC' tiam rezultas
Ĉi tiu ekvacio povas esti diskretigita. Estu specimenoj de la enigo kaj eligo prenitaj je egal-intervale situantaj punktoj de tempo, apartigitaj per daŭro Td. Estu la specimenoj de venen(t) prezentitaj per la vico (x1, x2, ..., xn), kaj estu specimenoj de vel(t) prezentitaj per la vico (y1, y2, ..., yn) kiu respektivas al la samaj punktoj de tempo. Tiam eblas skribi la ekvacion, kiu tamen estas nur proksimume ekvivalenta al la fonta, ĉar la diferencialado estas simple anstataŭigita per rilatumo de finiaj diferencoj; tiel ĝi priskribas fakte malsaman cirkviton:
La simileco al la fonta kontinua-tempa ekvacio estas pli bona se Td << τ.
Reordigo de termoj donas la rikurecan rilaton
aŭ
kie
Tio estas, ĉi tiu diskreta-tempa realigo de analogo de simpla RC malalta-pasa filtrilo estas la eksponente-pezita movanta averaĝo.
Per la difino pli supre donita, estas la glatiganta faktoro α, tia ke 0≤α≤1. La esprimo por α liveras la ekvivalentan tempan konstanton τ per la diskretiga periodo Td kaj glatiganta faktoro α:
Se α = 1/2, do la tempa konstanto estas egala al la diskretiga periodo. Se α << 1/2 do τ estas grave pli granda ol la diskretiga periodo, kaj Td ≈ ατ.

















