Senpintigita 5-ĉelo
| Senpintigita 5-ĉelo | |
 Figuro de Schlegel kun kvaredraj ĉeloj montritaj | |
| Speco | Uniforma plurĉelo |
| Vertica figuro | Egallatera triangula piramido (malregula kvaredro) (3 senpintigitaj kvaredroj kaj 1 kvaredro kuniĝas je ĉiu vertico) |
| Bildo de vertico | Bildo de vertico |
| Simbolo de Schläfli | t0,1{3,3,3} |
| Figuro de Coxeter-Dynkin | |
| Simbolo de Bowers | Tip |
| Verticoj | 20 |
| Lateroj | 40 |
| Edroj | 20 {3} 10 {6} |
| Ĉeloj | 5 kvaredroj (3.3.3) 5 (3.6.6) |
| Geometria simetria grupo | A4, [3,3,3] |
| Propraĵoj | Konveksa |
En geometrio, la senpintigita 5-ĉelo estas konveksa uniforma plurĉelo. Kiel la nomo sugestas, ĝi povas esti farita per tranĉo de la regula 5-ĉelo je 1/3 de la latera longo.
Dum la tranĉo la 5 kvaredraj ĉeloj de la fonta 5-ĉelo iĝas senpintigitajn kvaredrojn, kaj la novaj 5 kvaredraj ĉeloj aperas en lokoj de la originalaj verticoj.
Ĝi estas barita per 10 ĉeloj: 5 kvaredra, kaj 5 senpintigis kvaredra.
La senpintigis kvaredroj estas kunigitaj unu al la alia tra iliaj seslateraj edroj, kaj al la kvaredroj tra iliaj triangulaj edroj.
Projekcioj
[redakti | redakti fonton]La kvaredro-unua paralela projekcio de la senpintigita 5-ĉelo en 3-dimensian spacon estas jena:
- La projekcia koverto estas senpintigita kvaredro.
- Unu el la senpintigitaj kvaredraj ĉeloj projekciiĝa al la tuta koverto.
- Unu el la kvaredraj ĉeloj projekciiĝas al kvaredro situanta je centro de la koverto.
- Kvar malregulaj kvaredroj tuŝas la triangulajn edrojn de la koverto kaj estas koneksaj al la centra kvaredro per 4 radiusaj lateroj. Ĉi tiuj estas la bildoj de la ceteraj 4 kvaredraj ĉeloj.
- Inter la centra kvaredro kaj 4 seslateraj edroj de la koverto estas 4 neuniformaj senpintigitaj kvaredroj kiuj estas la bildoj de la 4 ceteraj senpintigitaj kvaredraj ĉeloj.
Ĉi tiu aranĝo de ĉeloj en projekcio estas analoga al aranĝo de edroj en la edro-unua projekcio de la senpintigita kvaredro en 2-dimensian spacon. Tiel la senpintigita 5-ĉelo povas esti konsiderata kiel la 4-dimensia analogo de la senpintigita kvaredro.
Bildoj
[redakti | redakti fonton]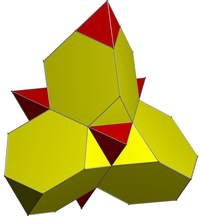 Reta hiperpluredro |
 Rektlinia sfera projekcio centrita je senpintigita kvaredro |
Alternativaj nomoj
[redakti | redakti fonton]- Senpintigita kvinĉelo
- Senpintigita 4-simplaĵo
Vidu ankaŭ
[redakti | redakti fonton]- Senpintigita 4-hiperkubo
- Senpintigita 16-ĉelo
- Senpintigita 24-ĉelo
- Senpintigita 120-ĉelo
- Senpintigita 600-ĉelo
- 5-ĉelo
- Uniforma plurĉelo
- Senpintigita kvaredro
Eksteraj ligiloj
[redakti | redakti fonton]- George Olshevsky, Kvinĉelo en Glossary for Hyperspace.

