Tri-seplatera kahelaro
| Tri-seplatera kahelaro | |
 Projekcio kiel diska modelo de Poincaré de la hiperbola ebeno. | |
| Speco | latero-transitiva |
| Vertica figuro | 3.7.3.7 |
| Bildo de vertico | 
|
| Simbolo de Wythoff | 2 | 7 3 |
| Simbolo de Schläfli | aŭ t1{7,3} |
| Figuro de Coxeter-Dynkin | |
| Geometria simetria grupo | [7,3] |
| Duala | Ordo-7-3 kvazaŭregula romba kahelaro |
| Bildo de duala | 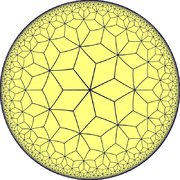
|
En geometrio, la tri-seplatera kahelaro estas duonregula kahelaro de la hiperbola ebeno. Estas du trianguloj kaj du (seplateroj, seplateras) alterna sur ĉiu vertico. Ĝia simbolo de Schläfli estas t1{7,3}.
La kahelaro povas esti konstruita per rektigo de la regula ordo-3 seplatera kahelaro aŭ per rektigo de la regula ordo-7 triangula kahelaro.
Vico de rilatantaj pluredroj kaj kahelaroj[redakti | redakti fonton]
La tri-seplatera kahelaro estas ero de vico de rektigitaj regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (3.n.3.n).
En ĉi tiu vico, la lateroj projekciiĝas en ĉefcirklojn de sfero je la pluredroj kaj en malfiniajn rektajn liniojn je la ebenaj kahelaroj.
 Okedro (3.3.3.3) |
 Kubokedro (3.4.3.4) |
 Dudek-dekduedro (3.5.3.5) |
 Tri-seslatera kahelaro (3.6.3.6) |
 Tri-seplatera kahelaro (3.7.3.7) |
 Tri-oklatera kahelaro (3.8.3.8) |
Duala kahelaro[redakti | redakti fonton]
La duala kahelaro estas ordo-7-3 kvazaŭregula romba kahelaro, farita el rombaj edroj, alterne kun 3 kaj 7 romboj ĉirkaŭ vertico.
Vidu ankaŭ[redakti | redakti fonton]
- Tri-seslatera kahelaro - kun vertica konfiguro 3.6.3.6
- Kvazaŭregula romba kahelaro - kun edra konfiguro V3.6.3.6
- Kahelaro de 2-dimensia ebeno
- Listo de unuformaj ebenaj kahelaroj
Referencoj[redakti | redakti fonton]
- Branko Grünbaum, Shephard G. C.. (1987) Tilings and Patterns - Kahelaroj kaj ŝablonoj. Novjorko: W. H. Freeman. ISBN 0-7167-1193-1.
Eksteraj ligiloj[redakti | redakti fonton]
- Eric W. Weisstein, Hiperbola kahelaro en MathWorld.
- Eric W. Weisstein, Hiperbola disko de Poincaré en MathWorld.
- Galerio de hiperbolaj kaj sferaj kahelaroj Arkivigite je 2013-03-24 per la retarkivo Wayback Machine
- KaleidoTile 3 - kleriga programaro por krei sferajn, ebenajn kaj hiperbolajn kahelarojn
- Hiperbolaj ebenaj kahelaroj Arkivigite je 2011-09-27 per la retarkivo Wayback Machine


