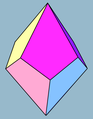
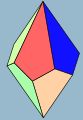
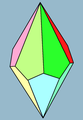
Kajtopluredro
| Kajtopluredro | |
| Speco | Aro de kajtopluredroj |
| Edra figuro | V3.3.3.n |
| Verticoj | 2n+2 |
| Lateroj | 4n |
| Edroj detale | 2n kajtoj |
| Geometria simetria grupo | Dnd |
| Propraĵoj | konveksa, edro-transitiva |
| Duala | n-latera kontraŭprismo |
La n-kajtopluredro, maldupiramido, kajtoedro, trapezopluredro aŭ trapezoedro estas la duala pluredro de neklina n-latera kontraŭprismo kun regulaj bazoj. Ĝiaj 2n edroj estas kongruaj kajtoj. La edroj estas simetrie lokitaj.
La nomo trapezopluredro estas iluzia ĉar la edroj ne estas trapezoj.
La n-ordo de la nomo ne referenco la edroj de la pluredro sed al ordigo de verticoj ĉirkaŭ la simetriakso. La duala n-kontraŭprismo havas du realajn n-plurlaterajn edroj.
n-latera kajtopluredro povas esti malkomponita en du egalajn n-laterajn piramidojn kaj n-lateran kontraŭprismon.
En tekstoj priskribantaj la kristalajn rutinojn de mineraloj, la vorto kajtopluredro estas ofte uzata por signifi la pluredron sciatan kiel deltosimila dudekkvaredro.
Formoj
[redakti | redakti fonton]Ĉe triangula kajtopluredro la kajtoj estas romboj, do triangula kajtopluredro estas romboedro kaj samtempe paralelepipedo. Ĝi estas kuboj skalita direkte de ĝia spaca diagonalo.
Kubo estas speciala okazo de triangula kajtopluredro kun kvadrataj edroj
La alia speciala okazo de triangula kajtopluredro estas tiu kun romboj kun anguloj de 60° kaj 120°. Ĝi povas esti malkomponita en du egalajn regulajn kvaredrojn kaj regulan okedron. Pro tio ke paralelepipedoj povas kaheligi spacon, do kombinaĵo de regulaj kvaredroj kaj regulaj okedroj povas kaheligi spacon.
Simetrio
[redakti | redakti fonton]La geometria simetria grupo de n-latera kajtopluredro estas Dnd de ordo 4n, escepte de kubo, kiu havas la pli grandan geometrian simetrian grupon Od de ordo 48, kiu havas 4 versiojn de D3d kiel subgrupoj.
La turna grupo estas Dn de ordo 2n, escepte de kubo, kiu havas la pli grandan turnan grupon O de ordo 24, kiu havas 4 versiojn de D3 kiel subgrupoj.
Ekzemploj
[redakti | redakti fonton]- Kristala sistemo de atomoj povas havi en kajtopluredrajn ĉeloj.
- La kvinlatera kajtopluredro estas havanta 10 edrojn pluredro kiu ne estas platona solido kaj kiu estas uzata kiel ĵetpluredro por generi hazardajn nombrojn 0 ... 9 aŭ 1 ... 10.
Vidu ankaŭ
[redakti | redakti fonton]Eksteraj ligiloj
[redakti | redakti fonton]- Eric W. Weisstein, Kajtopluredro en MathWorld.
- Virtualaj realaj pluredroj - la enciklopedio de pluredroj
- VRML modeloj [1] <3> Arkivigite je 2020-09-15 per la retarkivo Wayback Machine <4> Arkivigite je 2020-02-24 per la retarkivo Wayback Machine <5> Arkivigite je 2018-02-24 per la retarkivo Wayback Machine <6> Arkivigite je 2020-09-15 per la retarkivo Wayback Machine <7> Arkivigite je 2019-12-30 per la retarkivo Wayback Machine <8> [rompita ligilo] <9> Arkivigite je 2020-09-15 per la retarkivo Wayback Machine <10> Arkivigite je 2018-06-20 per la retarkivo Wayback Machine
- Notacio por pluredroj de Conway Provu: "dan", kie n=3,4,5... , ekzemple "dA5" estas kvinlatera kajtopluredro.
- Paperaj modeloj de kvarlatera (kvadrata) kajtopluredro Arkivigite je 2008-10-09 per la retarkivo Wayback Machine