120-ĉelo
| 120-ĉelo | |
 Figuro de Schlegel | |
| Speco | Konveksa regula plurĉelo |
| Vertica figuro | Kvaredro (3.3.3) |
| Bildo de vertico | 
|
| Simbolo de Schläfli | {5,3,3} |
| Figuro de Coxeter-Dynkin | |
| Verticoj | 600 |
| Lateroj | 1200 |
| Edroj | 720 kvinlateroj {5} |
| Ĉeloj | 120 dekduedroj (5.5.5) |
| Geometria simetria grupo | H4, [3,3,5] |
| Propraĵoj | Konveksa |
| Duala | 600-ĉelo |
En geometrio, la 120-ĉelo aŭ centdudekĉelo estas la konveksa regula plurĉelo kun simbolo de Schläfli {5,3,3}.
Ĝi povas esti konsiderata kiel la 4-dimensia analogo de la dekduedro.
La rando de la 120-ĉelo estas komponita el 120 dekduedraj ĉeloj kaj 4 el ili kuniĝas je ĉiu vertico. Kune ili havas 720 kvinlaterajn edrojn, 1200 laterojn kaj 600 verticoj. Estas 4 dekduedroj, 6 kvinlateroj, kaj 4 lateroj kuniĝantaj je ĉiu vertico. Estas 3 dekduedroj kaj 3 kvinlateroj kuniĝantaj je ĉiu latero.
La duala hiperpluredro de la 120-ĉelo estas la 600-ĉelo. La vertica figuro de la 120-ĉelo estas kvaredro.
Karteziaj koordinatoj[redakti | redakti fonton]
Karteziaj koordinatoj de 600 verticoj de la 120-ĉelo centrita je (0, 0, 0, 0) estas ĉiuj permutoj de
- (0, 0, ±2, ±2)
- (±1, ±1, ±1, ±√5)
- (±τ−2, ±τ, ±τ, ±τ)
- (±τ−1, ±τ−1, ±τ−1, ±τ2)
kaj ĉiuj paraj permutoj de
- (0, ±τ−2, ±1, ±τ2)
- (0, ±τ−1, ±τ, ±√5)
- (±τ−1, ±1, ±τ, ±2)
kie τ estas la ora proporcio (1+√5)/2.
Bildoj[redakti | redakti fonton]

|
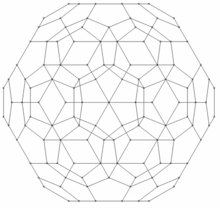
|
| Rektlinia sfera projekcio | Orta projekcio |
Vidu ankaŭ[redakti | redakti fonton]
- Uniforma plurĉelo
- Rektigita 120-ĉelo
- Senpintigita 120-ĉelo
- Dutranĉita 120-ĉelo
- Laterotranĉita 120-ĉelo
- Rektigitotranĉita 120-ĉelo
- Edrotranĉita 120-ĉelo
- Edroverticotranĉita 120-ĉelo
- Entutotranĉita 120-ĉelo
Referencoj[redakti | redakti fonton]
- H. S. M. Coxeter, Regulaj hiperpluredroj, 3-a. red., Doveraj Eldonoj, 1973. ISBN 0-486-61480-8.
- Kalejdoskopoj: Elektitaj skriboj de H.S.M. Coxeter, redaktita de F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Papero 22) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papero 23) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj II, [Math. Zeit. 188 (1985) 559-591]
- (Papero 24) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj III, [Math. Zeit. 200 (1988) 3-45]
- John Horton Conway kaj Michael Guy: Kvar-dimensiaj arĥimedaj hiperpluredroj, Paperoj de la Kolokvo sur Konvekseco je Kopenhago, paĝo 38 kaj 39, 1965
- Norman Johnson: La teorio de uniformaj hiperpluredroj kaj kahelaroj, Ph.D. Disertaĵo, Universitato de Toronto, 1966
Eksteraj ligiloj[redakti | redakti fonton]
- Eric W. Weisstein, 120-ĉelo en MathWorld.
- George Olshevsky, 120-ĉelo en Glossary for Hyperspace.
- 120-ĉelo (32) de konveksaj uniformaj plurĉeloj de George Olshevsky
- [2] Pri 120-ĉelo en regulaj hiperpluredroj de Marco Möller en R4
- 120-ĉelo Arkivigite je 2005-11-23 per la retarkivo Wayback Machine - iuj projekcioj de la 120-ĉelo al 2 dimensioj.
- 120-ĉela esploristo - libera interaga programo kiu permesas lerni pri la 120-ĉelaj simetrioj. La 120-ĉelo estas projekciata al 3 dimensioj kaj tiam bildigata per OpenGL.
- Hiperpluredroj Arkivigite je 2005-11-24 per la retarkivo Wayback Machine - projekcio de la 120-ĉelo al 3 dimensioj kun latentaj detaloj forprenitaj , meze en la paĝo.

