Ondosimilaĵo
En matematiko, ondosimilaĵo estas ondo-simila oscilado, kies amplitudo startas je nulo, pligrandiĝas, kaj tiam malpligrandiĝas reen al nulo. Ĝi povas tipe esti videbligita kiel lakona oscilado.
Ondosimilaĵo estas osciloforma signalo de finia longo (tempodaŭro), aŭ ĝi estas de malfinia longo sed rapide proksimiĝas al nulo kiam la tempa koordinato malproksimiĝas for de la ĉefa tempodaŭro de la ondosimilaĵo.
Ĝenerale, ondosimilaĵoj estas speciale konstruataj por havi specifajn propraĵojn, kiuj faras ilin utilajn por signal-prilaborado. Ondosimilaĵoj povas esti kombinitaj per kunfaldaĵoj (ŝovo, multipliko kaj sumo) kun donita signalo por ekstrakti informon pri la signalo.
Ondosimilaĵo estas matematika funkcio uzata por disdividi donitan funkcion aŭ kontinuo-tempan signalon en malsamajn skalajn komponantojn. Kutime unu povas asigni frekvencan bendon al ĉiu skala komponanto. Ĉiu skala komponanto povas tiam esti studata kun distingokapablo respektiva al ĝia skalo. Ondosimilaĵa konverto estas la prezento de funkcio per ondosimilaĵoj. La ondosimilaĵoj estas skalataj kaj movataj kopioj (nomataj kiel filinaj ondosimilaĵoj) de la fonta ondosimilaĵo (nomata kiel la patrina ondosimilaĵo). Ondosimilaĵaj konvertoj havas iujn avantaĝojn super tradiciaj konvertoj de Fourier por prezentado de funkcioj, kiuj havas nekontinuecojn kaj akrajn kulminojn, kaj por precize malkonstrui kaj rekonstrui finiajn ne-periodajn aŭ ne-senmovajn signalojn.
Ondosimilaĵaj konvertoj[redakti | redakti fonton]
En formalaj terminoj, ondosimilaĵa konverto estas prezento de kvadrato-integralebla funkcio kiel serio kun respekto al plena ortonormala aro de bazaj funkcioj, aŭ kun respekto al troplena aro aŭ kadro de vektora spaco, por la hilberta spaco de kvadrataj integraleblaj funkcioj.
Ondosimilaĵaj konvertoj estas klasifikitaj en diskretaj ondosimilaĵaj konvertoj kaj kontinuaj ondosimilaĵaj konvertoj. Ambaŭ diskreta ondosimilaĵa konverto kaj kontinua ondosimilaĵa konverto estas kontinua-tempaj (analogaj) konvertoj kaj povas esti uzataj por prezenti kontinuo-tempajn (analogajn) signalojn. Kontinuaj ondosimilaĵaj konvertoj operacias super ĉiuj (reelaj) eblaj skaloj kaj movoj, dum diskretaj ondosimilaĵaj konvertoj uzas specifan subaron de skaloj kaj movoj.
 |
 |
 |
Ĉiu ondosimilaĵa konverto povas esti konsiderata kiel formo de tempo-frekvenca prezento por kontinuo-tempaj (analogaj) signaloj kaj do estas iel simila al konverto de Fourier. Preskaŭ ĉiu praktike utila diskreta ondosimilaĵa konverto uzas diskreto-tempajn filtrilajn bankojn. Ĉi tiuj filtrilaj bankoj estas nomataj kiel la ondosimilaĵaj kaj la skalaj koeficientoj en ondosimilaĵa nomado. Ĉi tiuj filtrilaj bankoj povas havi filtrilojn kun finia impulsa respondo aŭ malfinia impulsa respondo. La ondosimilaĵoj formantaj kontinuan ondosimilaĵan konverton estas sub la necerteca principo de respektiva diskretiga teorio de analizo de Fourier: por donita signalo kun iu evento en ĝi, oni ne povas asigni samtempe akuratajn tempon kaj frekvencon al ĉi tiu evento. La produto de la necertecoj je tempo kaj frekvenco havas suban baron. Tial, en la rezulto de kontinua ondosimilaĵa konverto de ĉi tiu signalo, la evento okupas iun regionon en la tempo-frekvenca ebeno, anstataŭ nur unu punkto. Ankaŭ, diskretaj ondosimilaĵaj bazoj povas esti konsiderataj en la ĉirkaŭteksto de la aliaj formoj de la necerteca principo.
Ondosimilaĵaj konvertoj estas larĝe dividita en tri klasifikaĵojn: kontinuaj, diskretaj kaj multdistingokapablo-bazitaj.
Kontinuaj ondosimilaĵaj konvertoj[redakti | redakti fonton]
Kontinuaj ondosimilaĵaj konvertoj havas kontinuajn ŝovan kaj skalan parametrojn.
En kontinua ondosimilaĵa konverto, donita signalo de finia energio estas projekciita sur kontinuan familion de frekvencaj bendoj (aŭ similaj subspacoj de la Lp funkcia spaco ). Ekzemple la signalo povas esti prezentita sur ĉiu frekvenca bendo de formo [f, 2f] por ĉiuj pozitivaj frekvencoj f>0. Tiam, la originala signalo povas esti rekonstruita per taŭga integralado tra ĉiuj rezultantaj frekvencaj komponantoj.
La frekvencaj bendoj aŭ subspacoj (sub-bendoj) estas skalitaj versioj de subspaco je skalo 1. Ĉi tiu subspaco laŭvice estas en plejparto de situacioj generata per la ŝovoj de unu generanta funkcio , la patrina ondosimilaĵo. Kiel ekzemplo ĉi tiu funkcio por frekvenca bendo [1, 2] povas esti
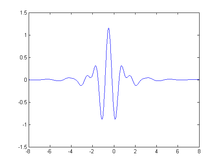
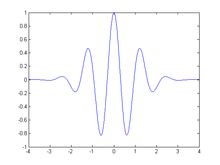
kun la (ununormigita) funkcio sinc. La aliaj ekzemploj de patrinaj ondosimilaĵoj estas:
 |
 |
 |
La subspaco de skalo a aŭ frekvenca bendo [1/a, 2/a] estas generata per la funkcioj (iam nomataj kiel infanaj ondosimilaĵoj)
kie a estas pozitiva kaj difinas la skalon kaj b estas iu reela nombro kiu difinas la ŝovon. La paro (a, b) difinas punkton en la dekstra duonebeno R+×R .
La projekcio de funkcio x sur la subspacon de skalo a tiam havas formon
kun ondosimilaĵaj koeficientoj
Diskretaj ondosimilaĵaj konvertoj[redakti | redakti fonton]
Diskretaj ondosimilaĵaj konvertoj havas diskretajn ŝovan kaj skalan parametrojn.
Estas kompute neeble analizi signalojn uzante ĉiujn ondosimilaĵajn koeficientojn. Tamen iam sufiĉas preni diskretan subaron de la supra duonebeno povi rekonstrui signalon surbaze de la respektivaj ondosimilaĵaj koeficientoj. Unu tia sistemo estas la afina sistemo por iuj reelaj parametroj a>1, b>0. La respektiva diskreta subaro de la duonebeno konsistas el ĉiuj punktoj (am, namb) kun entjeroj m kaj n. La respektivaj infanaj (idaj) ondosimilaĵoj estas tiam donataj kiel
Sufiĉa kondiĉo por la rekonstruado de ĉiu signalo x de finia energio per la formulo
estas ke la funkcioj formas striktan kadron de .
Multdistingokapablaj diskretaj ondosimilaĵaj konvertoj[redakti | redakti fonton]
En ĉiu diskreta ondosimilaĵa konverto, estas nur finia kvanto de ondosimilaĵaj koeficientoj por ĉiu barita ortangula regiono en la supra duonebeno. Ankoraŭ, ĉiu koeficiento postulas la pritakson de integralo. Por eviti ĉi tiun ciferecan komplikecon, oni bezonas iun helpan funkcion, la patran ondosimilaĵon . Plu, oni devas limigi a al esti entjero. Tipa elekto estas a=2 kaj b=1. La plej fama paro de patro kaj patrinaj ondosimilaĵoj estas la 4-frapa ondosimilaĵo de Daubechies.
De la patrina kaj patra ondosimilaĵoj oni konstruas la subspacojn
- , kie
kaj
- , kie
De ĉi tiuj oni postulas, ke la vico
formas multdistingokapablan analitikon de kaj ke la subspacoj ..., W1, W0, W-1, ... estas la perpendikularaj diferencoj de la pli supra vico, kio estas ke Wm estas la perpendikulara komplemento de Vm ene de la subspaco Vm-1. En analogeco al la diskretiga teoremo oni povas konkludi, ke la spaco Vm kun diskretiga distanco 2m plimalpli kovras la frekvencan bazan bendon de 0 al 2−m−1. Kiel perpendikulara komplemento, Wm proksimume kovras la bendon [2−m−1, 2−m].
De tiuj inkluzivecoj kaj ortecaj rilatoj sekvas la ekzisto de vicoj kaj kiuj kontentigas la identojn
- kaj
kaj
- kaj
La dua idento de la unua paro estas bonmaniereca ekvacio por la patra ondosimilaĵo φ. Ambaŭ paroj de identoj formas la bazon por la algoritmo de la rapida ondosimilaĵa konverto.
Patrina ondosimilaĵo[redakti | redakti fonton]
Por praktikaj aplikoj, oni preferas kontinue diferencialeblajn funkciojn kun kompakta subteno kiel patrinaj (prototipaj) ondosimilaĵaj funkcioj. Tamen, por kontentigi analitikajn postuloj (en la kontinua ondosimilaĵa konverto) kaj ĝenerale por teoriaj kaŭzoj, oni elektas la ondosimilaĵajn funkciojn de subspaco de la spaco . Ĉi tiu estas la spaco de mezureblaj funkcioj kiu estas absolute kaj kvadrate integraleblaj:
- kaj
Estado en ĉi tiu spaco certiĝas ke oni povas formuli la kondiĉoj de nula meznombro
kaj kvadrata normo 1
Por ke ψ estu ondosimilaĵo por la kontinua ondosimilaĵa konverto, la patrina ondosimilaĵo devas kontentigi kriterion de taŭgebleco (kio estas, lakse parolante, speco de duono-derivebleco) por ricevi stabilan inversigeblan konverton.
Por la diskreta ondosimilaĵa konverto, oni bezonas almenaŭ la kondiĉon ke la ondosimilaĵa serio estas prezento de la idento en la spaco . Plejparto de konstruoj de diskretaj ondosimilaĵaj konvertoj uzas la multdistingokapablan analitikon, kiu difinas la ondosimilaĵon per skala funkcio. Ĉi tiu skala funkcio mem estas solvaĵo de funkcia ekvacio.
En plejparto de situacioj estas utile al limigi ψ al esti kontinua funkcio kun pli granda kvanto M de nulaj momantoj, kio estas ke por ĉiu entjero m<M
Iuj ekzemplaj patrinaj ondosimilaĵoj estas:
 |
 |
 |
La patrina ondosimilaĵo estas skalata (aŭ plilarĝigita) je faktoro a kaj ŝovata je b por doni (en originala formulaĵo de Morlet):
Por la kontinua ondosimilaĵa konverto, la paro (a, b) varias super la plena duonebeno R+×R ; por la diskreta ondosimilaĵa konverto ĉi tiu paro varias super diskreta subaro de ĝi, kiu estas ankaŭ nomata kiel afina grupo.
Ĉi tiuj funkcioj estas ofte malĝuste nomataj kiel la bazaj funkcioj de la (kontinua) konverto. Fakte, same kiel en la kontinua konverto de Fourier, ne estas bazo en la kontinua ondosimilaĵa konverto. Tempo-frekvenca ekzegezo uzas malmulte malsaman formulaĵon (post Delprat).
Komparo kun kontinuo-tempa konverto de Fourier[redakti | redakti fonton]
La ondosimilaĵa konverto estas ofte komparata kun la konverto de Fourier, en kiu signaloj estas prezentataj kiel sumoj de sinusaj funkcioj. La ĉefa diferenco estas ke ondosimilaĵoj estas lokigataj en ambaŭ tempo kaj frekvenco, sed la norma konverto de Fourier estas lokigata nur en frekvenco. La mallongo-tempa konverto de Fourier estas pli simila al la ondosimilaĵa konverto, en tio ke en ĝi estas ambaŭ tempa kaj frekvenca lokigo, sed estas problemoj kun la frekvenca kaj tempa distingokapablo. Ondosimilaĵoj ofte donas pli bonan prezenton de signaloj per multdistingokapabla analitiko, kun balancita distingokapablo je momenteco kaj frekvenco.
La diskreta ondosimilaĵa konverto estas ankaŭ malpli kompute komplika, bezonante tempon O(N) kompare al O(N log N) por la rapida konverto de Fourier. Ĉi tiu komputa avantaĝo estas ne imanenta al la konverto, sed reflektas la elekton de logaritma divido de frekvenco, en kontrasto al la egale spacitaj frekvencaj dividoj ĉe la konverto de Fourier. Estas ankaŭ grave noti ke ĉi tiu komplikeco nur aplikas kiam amplekso de la filtrilo ne dependas de amplekso de la signalo. Ondosimilaĵo sen kompakta subteno kiel la ondosimilaĵo de Shannon devus postuli tempon O(N2). Simile, logaritma konverto de Fourier ankaŭ ekzistas kun komplikeco O(N), sed por ĝi la originala signalo devas esti specimenata logaritme en tempo, kio estas utila nur por certaj specoj de signaloj.
Difino de ondosimilaĵo[redakti | redakti fonton]
Estas pluraj manieroj difini ondosimilaĵon aŭ ondosimilaĵan familion.
Skalanta filtrilo[redakti | redakti fonton]
Perpendikulara ondosimilaĵo estas plene difinata per la skalanta filtrilo - malalta-pasiganta finia impulsa responda filtrilo de longo 2N kaj sumo 1. En duperpendikularaj ondosimilaĵoj, apartaj malkomponaĵa kaj rekonstrua filtriloj estas difinataj.
Por analitiko kun perpendikularaj ondosimilaĵoj la alta-pasiganta filtrilo estas kalkulita kiel la kvadratura spegula filtrilo de la malalta-pasiganta, kaj la rekonstrua filtrilo estas la tempa dorsflankigo de la malkomponaĵa filtrilo.
Ondosimilaĵoj de Daubechies kaj Symlet povas esti difinitaj per la skalanta filtrilo.
Skalanta funkcio[redakti | redakti fonton]
Ondosimilaĵo estas difinita per la ondosimilaĵa funkcio ψ(t) (kio estas la patrina ondosimilaĵo) kaj skalanta funkcio φ(t) (kio estas la patra ondosimilaĵo) en la tempa domajno.
La ondosimilaĵa funkcio estas efike bendo-pasiganta filtrilo kaj skaligo de ĝi por ĉiu nivelo duonigas la bendlarĝon. Ĉi tio kreas la problemon, ke por kovri la tutan spektron, malfinia kvanto de la niveloj devus esti bezonata. La skalantaj funkcioj filtras la plej suban nivelon de la konverto kaj certiĝas, ke ĉiu spektro estas kovrita.
Por ondosimilaĵo kun kompakta subteno, φ(t) povas esti konsiderata finia en longo kaj estas ekvivalento al la skalanta filtrilo g.
Ondosimilaĵoj de Meyer povas esti difinitaj per skalantaj funkcioj.
Ondosimilaĵa funkcio[redakti | redakti fonton]
La ondosimilaĵo nur havas prezenton en tempa domajna kiel la ondosimilaĵa funkcio ψ(t).
Meksikiaj ĉapelaj ondosimilaĵoj povas esti difinitaj per ondosimilaĵa funkcio.
Aplikoj[redakti | redakti fonton]
Ĝenerale, diskretaj ondosimilaĵaj konvertoj estas uzataj por datuma kunpremo se signalo estas jam specimenita, kaj kontinuaj ondosimilaĵaj konvertoj estas uzataj por signala analizo. Tial, diskretaj ondosimilaĵaj konvertoj estas kutime uzataj en inĝenierado kaj komputiko, kaj la kontinuaj ondosimilaĵaj konvertoj estas kutime uzataj en scienca esploro.
Ĝeneraligitaj konvertoj[redakti | redakti fonton]

Estas pluraj ĝeneraligitaj konvertoj, ĉe kiuj la ondosimilaĵa konverto estas speciala okazo.
Ekzemple, Joseph Segman aldonis skalon en la grupon Heisenberg, donante kontinuan konvertan spacon kiu estas funkcio de tempo, skalo, kaj frekvenco. La kontinua ondosimilaĵa konverto estas du-dimensia tranĉaĵo tra la rezultanta 3-dimensia tempo-skalo-frekvenca volumeno.
Alia ekzemplo de ĝeneraligita konverto estas la ĉirposimilaĵa konverto en kiu la kontinua ondosimilaĵa konverto estas ankaŭ dudimensia tranĉaĵo de la ĉirposimilaĵa konverto.
Grava aplika areo por ĝeneraligitaj konvertoj engaĝas sistemojn, en kiuj altfrekvenca rezolucio estas krita.
Frakciaj ondosimilaĵaj konvertoj estas bazitaj sur skalantaj funkcioj kiuj, malsimile al la normala kvazaŭ entjera ondosimilaĵa konverto, povas havi malfinian subtenon. Tamen, ili permesas ne tranĉadon de bazaj funkcioj, akuratan konsideron de randoj, kaj perfektan rekonstruon.
Listo de ondosimilaĵoj[redakti | redakti fonton]
Diskretaj ondosimilaĵoj[redakti | redakti fonton]
- Ondosimilaĵo de Beylkin
- BNC-ondosimilaĵo
- Ondosimilaĵo de Cohen-Daubechies-Feauveau, iam nomata kiel CDF N/P aŭ duperpendikulara ondosimilaĵo de Daubechies
- Ondosimilaĵo de Daubechies
- Ondosimilaĵo de Haar
- Ondosimilaĵo de Mathieu
- Ondosimilaĵo de Legendre
- Ondosimilaĵo de Villasenor
Kontinuaj ondosimilaĵoj[redakti | redakti fonton]
Reelo-valoraj[redakti | redakti fonton]
- Beta ondosimilaĵo
- Hermita ondosimilaĵo
- Hermita ĉapela ondosimilaĵo
- Meksikia ĉapela ondosimilaĵo
- Ondosimilaĵo de Shannon
Komplekso-valoraj[redakti | redakti fonton]
- Kompleksa meksikia ĉapela ondosimilaĵo
- Ondosimilaĵo de Morlet
- Ondosimilaĵo de Shannon
- Modifita ondosimilaĵo de Morlet
Historio[redakti | redakti fonton]
La evoluo de ondosimilaĵoj komenciĝis de kelkaj apartaj pensoj, startante de laboro de Alfréd Haar en komenco de la 20-a jarcento, kun la ondosimilaĵo de Haar (1909).
Rimarkindaj kontribuoj al ondosimilaĵa teorio estis malkovro de la kontinua ondosimilaĵa konverto de George Zweig en 1975 (originale nomata kiel la orela helika konverto kaj esplorata dum studado de reago de orelo al sono); formulaĵo de kiu estas nun sciata kiel la kontinua ondosimilaĵa konverto de Pierre Goupillaud, Alex Grossman kaj Jean Morlet (1982); frua laboro pri diskretaj ondosimilaĵoj de Jan-Olov Strömberg (1983); perpendikularaj ondosimilaĵoj kun kompakta subteno de Ingrid Daubechies (1988); multdistingokapabla kadro de Stephane Mallat (1989); tempo-frekvenco ekzegezo de la kontinua ondosimilaĵa konverto de Nathalie Delprat (1991), harmona ondosimilaĵa konverto de Newland (1993).
La vorto ondosimilaĵo estas de Jean Morlet kaj Alex Grossman en komenco de la 1980-aj jaroj. Ili uzis la francan vorton ondelette, kies signifo estas "malgranda ondo".
Vidu ankaŭ[redakti | redakti fonton]
- Kontinua ondosimilaĵa konverto
- Diskreta ondosimilaĵa konverto
- Rapida ondosimilaĵa konverto
- Senmova ondosimilaĵa konverto
- Frakcia ondosimilaĵa konverto
- Ondosimilaĵa paketa malkomponaĵo
- Ĉirposimilaĵa konverto
- Filtrila banko
- Konverto de Fourier
- Frakcia konverto de Fourier
- Mallongo-tempa konverto de Fourier
- Multdistingokapabla analizo, multdistingokapabla analitiko
- Skala spaco
- Onda paketo
- Ondosimilaĵa spaco
- Dimensia malpligrandiĝo
- Fourier-rilatantaj konvertoj
Eksteraj ligiloj[redakti | redakti fonton]
- Pri ondosimilaĵoj
- Notoj pri la ondosimilaĵoj
- Ondosimilaĵaj konvertoj
- [1][rompita ligilo]
- Michael Unser, Thierry Blu, "Frakciaj laŭpartaj interpolaj funkcioj kaj ondosimilaĵoj", SIAM recenzo, volumo. 42, Ne. 1 (Mar., 2000), pp. 43-67, Socio por Industria kaj Aplikita Matematiko, Stabila URL: [2]
- http://scienceworld.wolfram.com/biography/Zweig.html Biografio de George Zweig en Scienceworld.wolfram.com
- Difinado per skalanta funkcio
- Ondosimilaĵoj de Gilbert Strang, Amerika Sciencisto 82 (1994) 250-255. (tre mallonga enkonduko)
- Ondosimilaĵa digesto Arkivigite je 2020-09-29 per la retarkivo Wayback Machine
- Signala procezilo trajtanta ondosimilaĵajn manierojn de NASA Arkivigite je 2010-03-16 per la retarkivo Wayback Machine. Priskribo de signala & bilda procezada programaro de NASA kaj ligo por elŝuto
- 1-a NJIT Simpozio pri ondosimilaĵoj (30-a de aprilo, 1990) (Unua Ondosimilaĵa Konferenco en Usono)
- Dutermo-QMF ondosimilaĵoj, ondosimilaĵoj de Daubechies
- Ondosimilaĵoj farita Simpla[rompita ligilo]
- Kurso sur Ondosimilaĵoj donita je UC Santa Barbara, 2004
- La ondosimilaĵa lernilo de Polikar Arkivigite je 2018-04-30 per la retarkivo Wayback Machine
- Malfermita C++ kodo pri ondosimilaĵoj
- Enkonduko al ondosimilaĵoj Arkivigite je 2007-06-14 per la retarkivo Wayback Machine
- Ondosimilaĵoj Arkivigite je 2005-12-30 per la retarkivo Wayback Machine
- Kolekto de ligoj pri ondosimilaĵoj
- Akustika kaj elektromagnetaj ondosimilaĵoj de Gerald Kaiser[rompita ligilo]
- Gvidilo al ondosimilaĵoj
- Ondosimilaĵo-bazita bilda prilaboro Arkivigite je 2016-03-01 per la retarkivo Wayback Machine
- Tre baza ekspliko de ondosimilaĵoj kaj kiel konverto de Fourier rilatas al ĝi Arkivigite je 2007-08-29 per la retarkivo Wayback Machine
- Praktika gvidilo al ondosimilaĵo analizo kaj la ondosimilaĵa programaro en Fortran ktp. Noto ke la dekliva ondosimilaĵa pova spektro devas esti rektigita[rompita ligilo].
- Vortaro de ondosimilaĵaj nomoj
- Pitona ondosimilaĵa konverta pakaĵo - fonta kodo por komputado de 1D kaj 2D diskretaj ondosimilaĵaj konvertoj, senmovaj ondosimilaĵaj konvertoj kaj ondosimilaĵaj paketaj malkomponaĵoj.
- GNU-permesila biblioteko por n-dimensiaj diskretaj ondosimilaĵaj konvertoj[rompita ligilo]
- La frakcia laŭparta interpola funkcia ondosimilaĵa konverto
- [3][rompita ligilo]
- I. Daubechies: De kie ondosimilaĵoj venis Arkivigite je 2009-10-23 per la retarkivo Wayback Machine, Artikolo 74, Proceedings of the IEEE, Speciala eldono pri ondosimilaĵoj 84 (no. 4), pp. 510-513, aprilo 1996




























