Refrakta indico
La refrakta indico (ankaŭ refrakto-indico, aŭ pli simple refraktivo [1]) estas nocio de la optiko. Ĝi priskribas la refraktadon de unufrekvenca
elektromagneta ondo, ĉe trairo en diafana (travidebla) materialo kaj ĝi estas la rilato inter la fazorapido de la lumo en vakuo, kaj ties fazorapido en la respektiva medio:
Pri elektromagnetaj ondoj:
kie
- estas la relativa permitiveco de la medio,
- estas la relativa permeableco de la medio.
Plej ofte egalas al 1, do:
Materialo kun refrakta nombro de 1,5 = 3/2 havas lumrapidon precize 2/3-onan de la vakua lumrapido aŭ ĉirkaŭ 200.000 km/s.
La nocio "refrakta indico" venas el la nocio refrakto, kaj ties apero en la refrakta leĝo de Snell-Descartes. La fizika grando ne havas mezurunuon, ĝi estas nur kompara nombro.
Refraktivo de medio[redakti | redakti fonton]
| materialo | refrakta indico |
|---|---|
| vakuo | 1,0 |
| aero (terproksime) | 1,000292 |
| glacio | 1,31 |
| akvo | 1,33 |
| homa okulglobo | 1,35...1,42 |
| etanolo | 1,37 |
| magnezia fluorido | 1,38 |
| fluorspato | 1,43 |
| homa epidermo | 1,45 |
| Karbona kvarklorido | 1,46 |
| kvarca vitro | 1,46 |
| celuloza acetato (CA) | 1,48 |
| pleksia vitro (PMMA) | 1,49 |
| benzolo | 1,49 |
| kronvitro | 1,51 |
| COC (plastikaĵo) | 1,533 |
| PMMI (plastikaĵo) | 1,534 |
| kvarco | 1,54 |
| ŝtonsalo | 1,54 |
| polikarbonato (PC) | 1,58 |
| polistirolo (PS) | 1,58 |
| flinto | 1,60 |
| epoksida rezino | 1,60 |
| rubeno | 1,76 |
| organika okulvitro | 1,5-1,74 |
| vitro | 1,5-1,9 |
| zirkono | 1,92 |
| sulfuro | 2,00 |
| Zinka sulfido | 2,30 |
| diamanto | 2,47 |
| Titana dioksido (Anatas) |
2,52 |
| Titana dioksido (Rutil) |
2,71 |
| Titana dioksido (Rutil, 590 nm) |
3,10 |
| Plumba (II) sulfido (PbS, ĉe 590 nm) |
3,90 |
Oni povas kompari eĉ du indicojn de materialoj. La absoluta refrakta indico je libera spaco egalas al 1. Kutime uzeblas la aero, ĉar la refraktivo de aero estas preskaŭ 1 (ĉe marnivelo averaĝe 1,00029, en alto de 8 km nur 1,00011), tiel la refrakta indico de materialoj je aero preskaŭ samas kun tiu je la absoluta refrakta indico.
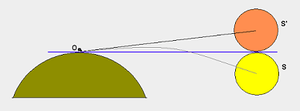
La eta refraktado de la aero devojigas la lumradiojn, venantajn el la steloj en la horizonto proksimume je 0,6° supren, kaj venantajn en 45° devojigas ankoraŭ je 0,017° (sed kiam la stelo estas al zenito neniu korekto necesas). La fenomeno nomiĝas astronomia refraktado kaj influas same la surteran mezuradon.
La valoro de la refraktivo dependas de la frekvenco (), de la premo () kaj de la temperaturo ().
Do pli ĝenerale oni povas skribi:
La ŝanĝo de aerorefraktivo laŭ la alteco kaŭzas miraĝojn.
La ĉi-apuda tabelo de la aero rilatas al temperaturo de 10 °C, premo de 100,3 kPa kaj ondolongo 0,589 m.
Pri lumo, la refrakta indico ne estas la sama laŭ diversaj koloroj (do laŭ diversaj frekvencoj). Tiu klarigas disigon de lumo per prismo, aŭ ĉielarkon per akvogutoj post pluvo.
Pri akvo, ŝajnas esti kontraŭdiron inter la refrakta indico skribita en la ĉi-apuda tabelo kaj la tabelo en la artilkolo pri dielektra permeableco: ne egalas al ; fakte ne estas kontraŭdiro, ĉar = 81 estas valoro kun tre malaltaj frekvencoj, dum = 1,33 korespondas al lumofrekvencoj, do tre altaj frekvencoj.
Kompleksa refraktivo[redakti | redakti fonton]
La dielektra permeableco (kiu ofte dependas de la ondolongo) estas simple la kvadrato de la (kompleksa) refraktivo en nemagneta medio (kies tia relativa permeableco egalas al unu). La refrakta indico estas uzita en optiko per la leĝo de Snell-Descartes; dum la dielektra permeableco estas uzita en elektromagnetismo per ekvacioj de Maxwell, kaj pri elektroniko.
Sciante ke kaj estas kompleksaj, kaj ke , , , and dependas de frekvenco:
oni povas dedukti la reelan parton kaj la imaginaran parton de la refraktivo ekde la kompleksaj partoj de la dielektra permeableco, per la sekvantaj kalkuloj
;
Plej ofte la imaginara parto estas tre malgranda kompare al , do:
Referenco[redakti | redakti fonton]
- ↑ (esperante) Refraktivo, el "Optiko" de János Sárközi (paĝoj 33 kaj sekvaj) Arkivigite je 2006-06-20 per la retarkivo Wayback Machine
Eksteraj ligiloj[redakti | redakti fonton]
- (angle)Datenoj pri refraktaj indicoj laŭ parametroj kaj kurboj laŭ ondolongoj
- (germane)Negativa refrakta indico ĉe la mikroondoj
- (germane)Speciala kristalo kun negativa refrakta indico

























