Elektromagnetismo


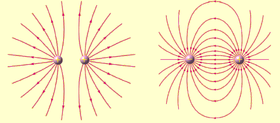
Elektromagnetismo estas tiu parto de fiziko, kiu okupiĝas pri la elektra kaj magneta kampoj kaj ĝiaj efikoj al ŝargaj partikloj.
La lorenca forto estas la elektromagneta forto, kiu interagas inter du elektraj ŝargaj partikloj. La ĝeneralaj ekvacioj, kiuj regas elektromagnetismon estas la ekvacioj de Maxwell, en kiuj aperas la lumrapido en vakuo:
Historio[redakti | redakti fonton]
Kun elektromagnetaj fenomenoj oni ekkonatiĝis jam dum la pratempo, per observado de fulmoj. La historio de la teorio de elektromagnetismo havas longan historion, de pratempo ĝis la nuna tago. Ekde la antikva epoko, la tuta mondo eksciis pri elektromagnetaj ondoj. En la ĉina antikva epoko ĉirkaŭ la jaro 400 antaŭ nia epoko, la majstroj de la valo de la diablo en la libro "La libro de magnetismo", (鬼谷 子) skribas: La magneto altiras la feron aŭ fero venas al ĝi. [1] Kaj ĉirkaŭ la jaro 1200, ĉinaj navigistoj uzis la elektromagnetan fenomenon per kompaso.[2]
Verkoj de William Gilbert kaj Benjamin Franklin[redakti | redakti fonton]
William Gilbert, en la jaro 1600, en sia verko De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure (Pri magnetoj, magnetaj korpoj kaj tera magneta kampo)[3] evidentigis la malsimilecojn inter la elektra kaj la magneta kampo. La influo de tiu eseo longe malrapidigis progreson en la esplorado de elektromagnetismo. Gilbert simple rimarkis, ke elektraj proprecoj ŝajnas foriĝi ju pli la temperaturo grandiĝas, kvankam magnetaj proprecoj ne malaperas tiel. En la sama verko Gilbert supozis, ke Tero mem ja estas granda magneto, kio ebligas kompasojn ĉiam indiki la nordan direkton.
Gilbert estis la unua, kiu uzis la grekan vorton ήλεκτρον (elektron), indikanta materialo kun elektrostatikaj proprecoj, por priparoli elektron.[4]
Benjamin Franklin ĉirkaŭ la jaro 1750 esploradis elektrostatikon. Multaj tiamaj fizikistoj ekkonatiĝis kaj interesiĝis pri elektro, danke al liaj eksperimentoj pri fulmoj kaj iliaj proprecoj.[5] Franklin publikigis hipotezon, laŭ kiu elektrajn proprecojn kaŭzis iu elektra likvaĵo per sia abundo aŭ malabundo en materialoj. Kvankam malĝusta, lia teorio komencis la ĝisnunan kutimon uzi la simbolojn + kaj - por priskribi elektrajn ŝarĝojn.[6]
Verkoj de Charles-Augustin de Coulomb kaj Carl Friedrich Gauss[redakti | redakti fonton]


En la jaro 1785, Charles-Augustin de Coulomb verkis tri memuarojn pri elektro kaj magnetismo,[7] en kiu li raportis, ke la forto inter du elektraj ŝargoj estas simila al la gravito, kaj ke la forto estas inverse proporcia al la kvadrato de la rekta distanco inter la partikloj, la ŝargo de ili estas proporcia al iliaj densecoj de elektra fluidaĵo. La vektora formulado de la kulomba leĝo laŭ la internacia sistemo de unuoj estas:
kie
- estas la elektra forto inter la partiklo 1 kaj la partiklo 2,
- estas la elektra kampo de la partikulo 2, en la loko de la partiklo 1,
- q1 et q2 estas la respektivaj elektraj ŝargoj de la partikloj 1 et 2,
- estas la distanco inter la partikloj 1 kaj 2, t.e.
- estas vektoro indikanta la direkton de la forto suferita de partiklo 1 fare de partiklo 2, kaj
- estas elektra konstanto, foje nomata kulomba konstanto.
Johann Carl Friedrich Gauss, matematikisto kaj sciencisto, en la jaro 1813, formulis la teoremon pri la inversa kvadrata leĝo de kampoj,[8] kaj deduktis sian gaŭsan leĝon, kiu poste konsideriĝis kiel aparta kazo de la nuna nomita teoremo de Stokes.[9] Aplikante la gaŭsan leĝon oni deduktas la kulomban leĝon, kaj per la diverĝenca teoremo (foje ankaŭ nomita gaŭsa teoremo) oni obtenas la gaŭsan elektrostatikan formulon sub la diferenciala formo de hodiaŭ:
kie estas la diverĝenco, estas la loka denso de elektra ŝargo ĉirkaŭ la konsiderita punkto, se estas pluraj elektre ŝargitaj partikloj en iu volumeno, sekve ke estas la rezulta elektra kampo kreita de tiuj partikloj.
Verkoj de Hans Christian Ørsted, Jean-Baptiste Biot, Félix Savart, André-Marie Ampère[redakti | redakti fonton]


Ĉirkaŭ la jaro 1820, Hans Christian Ørsted, Jean-Baptiste Biot, Félix Savart kaj André-Marie Ampère, pri la magneta forto sur elektraj dratoj en kiuj fluas elektraj kurentoj, faris similan leĝon je la kulomba leĝo.[10] Tiu leĝo koncernas la forton sur la drata 1 travojita de kurento 1 fare de fluksdenso kreita de kurento 2 en la drato 2, kaj estas esprimita laŭ la internacia sistemo de unuoj sub la jena vektora diferenciala formo:
kie
- estas la diferenciala vektoro proporcia al la longo de dratosegmento kaj la amplitudo de kurento 1 laŭ la direkto de ci-lasta,
- estas la magneta indukdenso en la loko de segmento 1 kreita de elektra kurento en segmento 2,
- et estas la elektraj kurentoj en la du segmentoj de dratoj,
- estas la distanco inter la du segmentoj 1 et 2,
- estas la direkto de segmento 2 al segmento 1,
- estas la vektora produto, kaj
- , kie estas la magneta konstanto.
Ĉirkaŭ la jaro 1850, George Gabriel Stokes kaj William Thomson ellaboris la teoremon de Stokes,[11] kiu ebligas transformi la leĝon de Biot-Savart sub la diferenciala nuna formo (foje nomita leĝo de Ampère)[12]:
kie estas la kirlo, estas la kurenta denseco pro la dratoj kaj estas la magneta indukdenso kreita de la kurentoj en la dratoj.
Verkoj de Michael Faraday[redakti | redakti fonton]


Kvankam la leĝoj de Coulomb kaj Biot-Savart priskribas la elektran kaj magnetan kampojn, la nocio de kampo mem estas originale koncepto de Michael Faraday, profesoro de kemio ĉe la Reĝa Instituto de Britio en 1813. Li instruis kaj eksperimentis pri elekrtromagnetismo kaj kemio ĝis la jaro 1860.[13] Antaŭ li, la agadoj de la gravito laŭ la distanco estis supozataj similaj je la elektra kaj magneta fortoj, sed Faraday koncipis teorion, laŭ kiu pri tiaj fortoj la faktoro tempo devu esti konsiderata por komplete priskribi la fenomenojn. Sur tiuj studterenoj, Faraday inventis la koncepton de linioj, kaj tiam montrigis la liniojn de magnetaj kampoj, kiuj provizis la fontoj de la ampera cirkvita leĝo, fare de cirklaj linioj ĉirkaŭ drato travojita de kurento.[14] Aplikante la gaŭsan teoremon al fontoj de magnetaj kampoj, li obtenis la gaŭsan leĝon pri magnetismo:[15]
Faraday ankaŭ produktis unu kampoteorion enkorpigantan ĉiujn kampojn, por ke ĝi estu universala. Por fortigi ĉi tiun hipotezon, necesis respondi al la demando, kiel transformi la gravitajn, elektrajn kaj magnetajn kampojn en energion. Fine, Faraday malkovris kiel transformi magnetan forton al elektra forto. Anstatauante la magnetan kampon per elektra, Faraday kreis duan leĝon (poste nomita leĝo de Maxwell-Faraday), sub la vektora diferenciala formo, esprimita laŭ la internacia sistemo de unuoj:
kie estas parto de la elektra kampo kreita de ŝanĝiĝanta magneta kampo.[16] Tiu ĉi principo estas bazo de la tuta elektromagnetismo kaj de elektraj motoroj.
Verkoj de James Clerk Maxwell kaj Heinrich Rudolf Hertz[redakti | redakti fonton]

James Clerk Maxwell, kiu aparte admiris Michael Faraday,[17] ellaboris diversajn elektromagnetajn kampajn ekvaciojn en sistemo de raciaj ekvacioj poste nomitaj ekvacioj de Maxwell.[18] Kiel Faraday, Maxwell proponis korektadon al la leĝo de Ampère, kaj klarigis ke ŝanĝanta magneta kampo kreas elektran kampon. La vektora diferenciala formo de la leĝo de Ampère, esprimita laŭ la internacia sistemo de unuoj, tiele korektita de Maxwell estas:
Ekde la jaro 1861, Maxwell disvolvis tiun korekton al aliajn ekvaciojn en la kunteksto de elektromagnetaj ondoj.[19] El la ekvacioj de Maxwelll intervenas la lumrapido en vakuo kaj rezultas diversaj ecoj de lumaj ondoj, Maxwell supozis la elektromagnetajn ondojn mem esti lumo. Per sia verko de 1865 A Dynamical Theory of Electromagnetic Field (Dinamika teorio pri elektromagneta kampo), en kiu liaj ekvacioj traktis la interrilatojn de elektra kaj magneta kampoj fare de iliaj evoluoj laŭ la tempo, li iniciatis novan branĉon de elektromagnetismo la klasika elektrodinamiko.[20] Fine de jaro 1887, Heinrich Rudolf Hertz per genia elektromagneta eksperimento konfirmis la naturon de lumo.[21]
Verkoj de Joseph John Thomson kaj Hendrik Antoon Lorentz[redakti | redakti fonton]

Malgraŭ ke la fulmoj kaj la fluoj estis antaŭe studitaj, la naturo de kelkaj el ili restis en dubo. Ĉu la elektra fluo originas de partikloj aŭ de fluido el la etero? Per eksperimentoj pri katodaj radioj en malplenigitaj boteloj Joseph John Thomson klarigis en 1897, ke la eroj formintaj la katodajn radiojn kaj elektron estis partikloj kun la plej malgrandaj masoj kaj negativaj ŝargoj, kiuj nomiĝas elektronoj,[22] la nomo proponita de George Johnstone Stoney en la jaro 1881 por la malgranda kvanto da elektra ŝargo.[23]Tiun malkovron konfirmis Joseph J. Thomson, kaj la elektran ŝargon de elektrono zorgeme mezuris kaj determinis Robert Andrews Millikan en 1909:[24]
- .
Antaŭe, ĉiuj leĝoj de la fiziko estis interpretitaj el la perspektivo de fortoj inter materiaj korpoj aŭ inter ili kaj la etero, sed en la jaroj 1890 - 1905 la leĝoj de la fiziko interpretiĝis laŭ la perspektivo de fortoj inter partikloj subatomaj aŭ elementaj kiel la elektronoj, kiuj konsistigas la konkretan materion. Dum tiuj jaroj, Hendrik Antoon Lorentz faris hipotezon, laŭ kiu la elektra fluo konsistas el movaj elektraj ŝargoj, kaj starigis la lorencan leĝon pri la elektromagneta forto inter elementaj partikloj. [25] Formulata en unuoj de la Internacia sistemo de unuoj lia leĝo skribiĝas:
kiei estas la rapido (relative al la senmova etero) de elementaj partikloj kun ŝargo q. De tiu formulo oni povas dedukti la laplacan forton. Lia elektronika teorio klarigis multajn ecojn de materio, eĉ pri relativeco, e.g. longo-kuntiriĝon de FitzGerald-Lorentz. [26]
Teorio de la relativeco, fotoelektra efiko kaj verkoj de Albert Einstein[redakti | redakti fonton]

Hendrik Lorentz en sia elektromagneta teorio, supozis ekzistantan sistemon de koordinatoj fiksitan al senmova etero; dum la jaro 1903 li trovis siajn lorencajn transformojn aplikatajn al koordinatsistemoj, kaj asertis ke la rezultantaj magnetaj kaj elektraj kampoj el la ekvacioj de Maxwell estas samaj en transformitaj aŭ ne transformitaj koordinatsistemoj.[27] Li sekvis la hipotezon de Augustin Jean Fresnel pri ekzisto de senmova etero, kiu libere penetras en la korpojn. Tiu supozo formis la bazon de ĝenerala teorio de elektraj kaj optikaj fenomenoj pri movaj korpoj. Sed laŭ tiu etero, la lumrapido devu ŝanĝi rilate al aliaj moviĝantaj koordinatsistemoj, kio kontraŭdiras la ekvaciojn de Maxwell, per kiu lumrapido estas konstanta.
Fine, en 1905, Albert Einstein trovis, ke nur du aksiomoj estas necesaj kaj sufiĉaj por derivi la lorencajn transformojn:[28] la principo de relativeco originale formulita de Galileo Galilei[29] kaj la konstanteco de la lumrapido, konata ekde la jaro 1887 de Albert Abraham Michelson kaj Edward Williams Morley en ĉiuj inerciaj koordinatsistemoj.[30] Fine, Einstein starigis la teorion de la speciala relativeco, demonstrante la transformojn de Lorentz el la bazo de ekvacioj de Maxwell kaj indikante, ke necesis diversaj amendoj de la neŭtona mekaniko.[31] El tiu ĉi perspektivo, la relativeca magneta kampo nature ekestas de la elektra kampo pro movo de koordinatsistemo..
Por Lorentz povas ekzisti senmova referenca etero, sed Einstein malakceptis tiun supozitan eteron kaj demonstri ke la lumo estas formita de moviĝantaj fotonoj sendepende de iu ajn nocio de etero.[32] Laŭ la teorio de Einstein, la energio E de fotono estas:
kie f estas la frekvenco de la elektromagneta ondo asociita kaj estas la konstanto de Planck. La nocio de fotono multe klarigis multajn fenomenojn, e. g. pri la fotoelektra efiko antaŭe studita de Heinrich Hertz kaj Philipp Lenard.[33]
Kvantuma kampa teorio kaj verkoj de Paul Dirac[redakti | redakti fonton]

Unue, Ejnŝtejno neis la ekziston de etero, sed ĉirkaŭ la jaro 1920 li mem trovis la ideon de etero necesa por sia ĝenerala teorio de relativeco pro lokaj interagoj kaj trans distancaj agadoj.[34] La etero de Ejnŝtejno estis simple la sidejo de elektromagnetaj kaj gravitaj kampoj kaj konsistiĝis nek el materio nek el eroj kun distintigiĝa pozicio. Baldaŭ post la eksperimento de Geiger-Marsden,[35] la fizikisto Ernest Rutherford konstatis, ke, aplikante nur la teoriojn de Maxwell kaj Lorentz al la elektronoj en atomoj, priskribeblas kial elektronoj restas kaptitaj en la kerno.[36] Tial, la kvantuma mekaniko naskiĝis laŭ tiaj novaj principoj.[37]
Paul Dirac, kies la granda verko Principia Mechanicae Quanticae (Principoj de kvantuma mekaniko) estas disvolvita en 1930,[38] kreis la unuan kontentigan teorion de la kvantuma elektrodinamiko, en kiu la fotono reprezentas la plej malgrandan kvanton da energio, kiu donas kaj kaptas la elektromagnetan kampon. El la nocio de fotono de Ejnŝrtejno, li trovis ke la eblaj energioj de elektromagneta ondo estas:
kie n estas entjero; rezultas do diskretaj valoroj de fotonoj. Poste, Richard Feynman, Freeman Dyson, Julian Schwinger kaj Sin-Itiro Tomonaga ege antaŭenirigis la teorion de la kvantuma elektrodinamiko dum la 1940-aj jaroj , kreante la unuan kontentigan teorion, pri kiu elektronoj, pozitronoj kaj fotonoj estas kreitaj kaj detruitaj el etero (aŭ kvantuma kampo).[39] Sekve, ili trovos fizikajn partiklojn, la eroj kaj de la etero kaj de la kampo, kiuj el ĉi-lastaj obtenas energion. Ne eblas konstati la diferencon inter ilia etero kaj la referenca senmova etero de Lorentz.
Paul Dirac estas konsiderita la fondinto de la kvantuma elektrodinamiko, li estis la una uzi la terminon. Komence de la 1940-aj jaroj enkondukiĝis la nocio de polarizo de vakuo (reorientiĝo de mallongedaŭraj partiklo-antipartiklo-paroj), pro tia fenomeno, kiu kontraŭdiras lian dirakan ekvacion, el kiu li antaŭvidis la antipartiklojn.
En 1931, Paul Dirac asertis, ke la ekzisto de magnetaj unupolusoj en la universo estis akordigebla kun la ekvacioj de Maxwell kaj kun la observataj kvantumigitaj elektraj ŝargoj ("negativa" en negatono kaj "pozitiva" en pozitono).[40]. tiu propono ricevis multan atenton, sed neniu konvinka evidenteco ekzistas pri la ekzisto de magneta unupoluso. Ĝis nun oni konsideras, ke estas ĉiam samtempe "nordaj magnetaj polusoj" kun ties kontraŭaj "'sudaj magnetaj polusoj".
Unuoj en la ekvacioj de elektromagnetismo[redakti | redakti fonton]
Ĉiuj sistemoj havas kiel bazajn unuoj metro, kilogramo kaj sekundo, aŭ frakcio de ili. Laŭ la sistemo la ekvacioj ŝanĝas por priskribi la elektromagnetajn fenomenojn.
La hodiaŭa sistemo de unuoj[redakti | redakti fonton]
La sistemo internacia de unuoj (aŭ SI aŭ ankoraŭ MKSA, reference al la mallongigoj de metro, kilogramo, sekundo, ampero) estis kreita ĉirkaŭ la jaro 1960[41] estas uzata de tiam kiel mezurunuoj de laboratorioj.
La ĉefaj unoj de tiu sistemo estas la metro (m), kilogramo (kg), sekundo (s) kaj ampero (A)[42]. La ampero estas difinita el la ampera forto tiele: ampero estas tia kurento ke, por du paralelaj konduktiloj kun konstanta kurento de 1 ampero en ĉiu, situantaj je 1 metro aparte unu de la alia en vakuo, la forto, al kiu estas submetita ĉiu konduktilo kun longo 1-metra estas precize 2×10-7 N, sekvas (kiel vidite supren) ke:
La unuo de elektra ŝargo, la kulombo (C), estas tiam difinita kiel la kvanto da ŝargoj moviĝantaj eksteren pro fluo de kurento je unu ampero dum unu sekundo; de tiu difino sekvas, ke , . La unuo de magneta indukdenso estas la teslo (T) , kies la rilato kun la derivataj kaj bazaj unuoj estas:
- [Teslo]
kaj la lorenca forto skribiĝas (kiel vidita supren):
La malnova sistemo de unuoj[redakti | redakti fonton]
La gaŭsa sistemo (aŭ CGS, reference al la mallongigoj de centimetro, gaŭso, sekundo) estas la plej malnova sistemo kreita ĉirkaŭ la jaro 1874.[43] Multaj fizikistoj hodiaŭ ankoraŭ preferas ĝin, ĉar per tiu gaŭsa sistemo ili povas uzi (pri vakua medio) la saman valoro por la magneta indukdenso esprimata en gaŭsoj kaj la magneta kampo esprimata en orstedoj. Estis do ne grave do konfuzi unun nocion kun alia; sed la konfuzo persistis maloportune kun la nova sistemo de unoj, kio ne plu taŭgas.
La ĉefaj unuoj de tiu sistemo estas:[44] la centimetro (cm), gramo (g), sekundo (s), kaj franklino (Fr). La unuo de elektrostatika ŝargo, la franklino, estas difinita tiel, ke pri du ŝargoj je unu centimetro de unu al alia la forto inter ili estu de unu dino; sekvas, ke la kulomba konstanto en la kulomba leĝo estas precize egala al 1:
Ankaŭ la unuo de magneta indukdenso estas la gaŭso (G), kies la rilato kun la franklino estas:
- [Gaŭso]
Kaj la lorenca forto skribiĝas:
kie co estas la lumrapido. Per tiaj difinoj, se oni aplikas la ekvaciojn de Maxwell, ili simplifiĝas sen la elektra konstanto nek la magneta konstanto, e.g. la ekvacio de Maxwell-Ampere skribiĝas:
Konceptoj[redakti | redakti fonton]
- La magneta fluksdenso, foje nomata simple magneta kampo estas fizika grando de elektro-dinamiko. Ĝi estas la area denso de la magneta flukso kiu trafluas orte difinitan elementon de surfaco. La magneta fluksdenso – same kiel la elektra indukdenso – estas direktita grando, do vektoro.
- La magneta kampintenso (formulsigno H) estas vektora grando, kiu karakterizas la fortefikon kaj la direkton en ĉiu punkto de magneta kampo. En vakuo ĝi egalas al la kvociento de magneta fluksdenso per la induktokonstanto. [45] :
- La magnetado estas fizika grando kiu karakterizas la la magnetan staton de materialo. Ĝi estas vektoro egala pri grandeco kaj direkto al la kvociento de la magneta momanto de iu elemento per ĝia volumeno :[46].
La magnetado priskribas la rilaton inter la magneta fluksdenso kaj la magneta kampintenso :
Tie estas la magneta konstanto kaj la magneta permeablo. En diamagnetaj materialoj estas la magnetado direktiĝas kontraŭe al la estiganta kampo; en paramagneta materialo estas sekve magnetado kaj kampo estas la samdirektaj.
- La magneta momanto en fiziko estas vektora grando, kiu mezuras la intenson de magneta dupoluso. Al magneta momanto en ekstera magneta kampo kun fluksdenso agas la tordmomanto
kiu turnas ĝin al la direkto de la kampo. Ĝia potenciala energio dependas de la angulo inter la direkto de la kampo direkto kaj la magneta momanto:
Referencoj[redakti | redakti fonton]
- ↑ Li Ŝu-hua, “Origine de la Boussole 11. Aimant et Boussole,” ("Origino de la kompaso"), ĵurnalo Isis, volumo 45, n-ro 2. (julio 1954), p. 175. (france)
- ↑ Ekz. en la verko Pingzhou Ke Tan ("ĉetablaj interparoloj de Pingzhou") de Zhu Yu en la jaro 1117 skribitas: "La navigisto konas geografion, observas la stelojn nokte, kaj la sunon tage; kiam malhelas kaj nubas, li rigardas la kompason."
- ↑ Vidu "De Magnete" kaj memorfeston pri la 400-a datreveno de tiu verko far David J. Sterna"400 Years of "De Magnete": Commemorating the 400th anniversary of "De Magnete" by William Gilbert of Colchester," Granda magneto, la Tero.(angle)
- ↑ La termino "elektro" kaj lia greka origino elektrono estas priskribitaj en paĝoj 31-33 "Notes on the De Magnete of D. William Gilbert," (Notoj pri De Magnete) skribitaj de Silvano P. Thompson kaj aliaj, Londono je 1901, kaj en "On the Magnet by William Gilbert," verkita de Derek J. Price (Novi Eboraci: Basic Books, 1958) denove produktita (angle).
- ↑ "Eksperimentoj kaj Observoj pri Elektro farita ĉe Filadelfio en Usono, de Benjamin Franklin, LLD kaj FRS", F. Newbery Londono, M.DCC.LXXIV "vidu ankaŭ memuaron "400 jaroj de Benjamin Franklin kaj fulmoŝirmilo" Arkivigite je 2006-01-10 per la retarkivo Wayback Machine skribitan de E . Philip Krider.
- ↑ Hence have arisen some new terms among us: we say B,(and bodies like circumstanced) is electrified positively; A, negatively. Or rather, B. is electrified plus; A, minus. (Sekve ŝprucis novaj terminoj inter ni, ni diros B (kaj korpoj ŝajnantaj) estas elektrizita pozitive; A negative. Aŭ prefereble B estas elektrizita plus; A, minus. En unu el aliaj leteroj de Benjamin Franklin senditaj al Petro Collinson: letero 2 de Benjamin Franklin, Esq.; Filadelfio al Peter Collinson, Esq.; F. R. S. Londono, 1747.
- ↑ C.-A. Kulombo, "Unua Memuaro pri Elektro kaj Magnetismo," Historio de la Reĝa Akademio de Sciencoj, 569-577, 1785 "Dua Memuaro pri Elektro kaj Magnetismo," Historio de la Reĝa Akademio de Sciencoj, 578-611, 1785 "Tria Memuaro pri Elektro kaj Magnetismo," Historio de la Reĝa Akademio de Sciencoj, 612-638, 1785. Vidu ankoraŭ "Kolekto da artikoloj rilataj al fiziko,...volumo I, Memuaroj de Kulombo" p. 146, kie Kulombo konkudis: Que l'action, soit répulsive, soit attractive de deux globes électrisés et, par conséquent, de deux molécules électriques, est en raison composée des densités du fluide électrique des deux molécules électrisées et inverse du carré des distances (Ke ago , aŭ forpuŝa, aŭ altira de du elektrizita globoj kaj, sekve, de du elektraj molekuloj, estas proporcia al la densecoj de la elektra fluidaĵo en la elektrizitaj molekuloj kaj inverse proporcia al la kvadrato de la distanco). (france)
- ↑ Carl Friedrich Gauss, "Teorio de altiro de homogenaj sferaj korpoj, je marto 1813, en Werke, volumo 5, paĝoj 3-24 en Universitätsbibliothek Göttingen - Digitalisierungszentrum (germane)
- ↑ La "teoremo de Stokes" estis fakte trovita de William Thomson; vidu ankaŭ paĝojn en:Stokes' theorem kaj Teoremo de Stokes.
- ↑ Malgraŭ ke Biot, Savart kaj Ampèrej ĉiuj partoprenis en tiu formo de la leĝo, la formulo nur al la leĝo pri la magneta formulaĵo estis nomita laŭ nur la nomoj de Biot kaj Savart; Oeuvres imprimées d'Ampère (Presitaj verkoj de Ampère ,André-Marie Ampère), @.ampère et l'histoire de l'électricité (france); kaj L. Pearce Williams, "Ampère, André-Marie", Dictionary of Scientific Biography 1:139-147 (Novi Eboraci: Charles Scribner's Sons, 1970) (angle); kaj la angla paĝo en:André-Marie Ampère.
- ↑ Vidu referencon [9] supre.
- ↑ Ĉi tiu ekvacio estas ekvivalenta al la leĝo de Biot-Savart kaj nomiĝas leĝo de Ampère. Kiel la leĝo de Biot-Savart, ĝi validas nur pri statikaj kondiĉoj; poste, James Clerk Maxwell korektis ĝin por la kazo de ŝanĝiĝantaj kurentoj, (vidu sube).
- ↑ Biografio de Michael Faraday skribita de L. Pearce Williams Michael Faraday: A Biography (Da Capo Press, 1987, ISBN 0-306-80299-6) (angle).
- ↑ Fakte, Faraday diris, ke li pensis pri la magnetaj kampoliniojn, en sia verko, "Pri la naturo de la linioj de fortoj", ((angle): "On the physical character of the lines of force") ,1852: "I cannot conceive curved lines of force without the conditions of a physical existence in that intermediate space" (Mi ne povas koncepti kurban linion de forto sen kondiĉoj de "fizika esto" en tiu interspaco).
- ↑ Vidu noton[8] supran.
- ↑ En komentario de laboratorio, Faraday priskribis en aŭgusto 1831 eksperimenton pri indukto de sparko inter du izolitaj cirkvitoj : "Have had an iron ring made (soft iron), iron round and 7/8 inches thick and ring 6 inches in external diameter. Wound many coils of copper wire round one half, the coils being separated by twine and calico. . . . Will call this side of the ring A . . . on the other side but separated by an interval was wound wire in two pieces together amounting to about 60 feet in length, the direction being as with the former coils; this side call B . . . continued the contact of A side [primary] with battery but broke and closed alternately contact of B side [secondary] with flat helix. No effect at such times on the needle [of a galvanometer connected to B side]—depends on the change at battery side. Hence is no permanent or peculiar state of wire from B but effect due to a wave of electricity caused at moments of breaking and completing contact at A side. Tried to perceive a spark with charcoal at flat helix junction B side but could find none. Wave apparently very short and sudden."(Tiu paragrafo estis prenita el la fonto [13] supre, p. 182.)
- ↑ En 1857, Faraday skribis al Makxwell, ke li estis la unua homo, pri kiu la ideo de korpoj agantaj foren estis asertita, kiel principo tute kredebla: you are the first person in whom the idea of bodies acting at a distance by throwing the surrounding medium into a state of constraint has arisen, as a principle to be actually believed in . . . nothing is clearer than your description of all sources of force keeping up a state of energy in all that surrounds them.
- ↑ J. C. Maxwell, A Dynamical Theory Of The Electromagnetic Field (Dinamika teorio de eletromagneta kampo), 1865, Pars 1, Pars 2, Pars 3, Pars 4, Pars 5, Pars 6; Vidu ankaŭ la modernan analizon de Andre Waser, On the Notation of Maxwell's Field Equations (Pri la notacio de ekvacioj de Maxwell), 2000, kaj anglajn paĝojn Victorian Web: James Clerk Maxwell kaj en:James Clerk Maxwell.
- ↑ Vidu paĝon 22 en part III skribita en la jaro 1861 'J. C. Maxwell, On Physical Lines of Force (Pri fizikaj linioj de forto),The London, Edinburg kaj Dublin Philosophical Magazine kaj Journal of Science, Ser. 4, marto, aprilo, kaj majo 1861. (angle)
- ↑ James Clerk Maxwell (1865). A dynamical theory of the electromagnetic field (Dinamika teorio pri elektromagneta kampo) (PDF) (angle). Philosophical Transactions of the Royal Society of London 155 p. 459–512. COI:1865RSPT..155..459C. (Tiu artikolo kunigita, la 8-an de decembro 1864, de prezento de Maxwell al la Reĝa Societo de Londono).
- ↑ Electric waves: being researches on the propagation of electric action with finite velocity through space (Elektraj ondoj: esploroj pri propagado de elektra agado per finia rapido tra spaco) de Heinrich Rudolf Hertz; obtenebla ankaŭ per Cornell University Library Digital Collections.
- ↑ Vidu la lekcion pri Nobel-premiito Joseph Thomson, kie estas priskribita lia identigo de ekzistanta elektrono.(angle)
- ↑ G. Stoney, On The Physical Units of Nature (Pri fizikaj unoj de naturo), Phil.Mag. 11, 381-391, 1881. (angle)
- ↑ Vidu la lekcion pri la Nobel-premiito Robert A. Millikan, kiu indikas ke Millikan determinis precize la ŝargon de elektrono. (angle)
- ↑ Vidu la lekcion pri la Nobel-premiito Hendrik Lorentz. (angle)
- ↑ George F. FitzGerald, "La vento kaj la tera atmosfero," Science 13, 390, 1889, Henrik A. Lorentz pubid = 615 & view = image & startrow = 1 "Elektromagnetaj fenomenoj en sistemo moviĝanta kun ajna rapido malpli granda ol tiu de lumo", 6, 1903-1904, p. 809-831, 1904. (angle)
- ↑ Vidu la notojn malsuprajn.
- ↑ A. Einstein, Zur Elektrodynamik bewegter Körper (Pri elektrodinamiko de movaj korpoj), Annalen der Physik 17, p. 891-921, 1905. (germane)
- ↑ Galileo Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla meccanica (Paroladoj kaj matematikaj demonstroj de du novaj sciencoj pri mekaniko), Nederlando, 1638; vidu ankaŭ la anglan paĝon en:Galileo's Ship.
- ↑ [https://web.archive.org/web/20150715063415/https://www.aip.org/history/gap/PDF/michelson.pdf Arkivigite je 2015-07-15 per la retarkivo Wayback Machine A. A. Michelson and E.W. Morley, Philos. Mag. S.5, 24 (151), 449-463, 1887].
- ↑ A. Einstein, Ist die Trägheit eines Körpers von seinem Energiegehalt abhängig? (Ĉu la maso de korpoj dependas de ilia energio?), Annalen der Physik 18, 639-641, 1905; kaj vidu la lekcion pri la Nobel-premiito Albert Einstein, Fundamental Ideas and Problems of the Theory of Relativity (Fundamentaj ideoj kaj problemoj de la teorio de la relativeco).
- ↑ A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (Pri produkto kaj transformo de lumo laŭ heŭristika vidpunkto), Annalen der Physik 17, 132–148, 1905. Arkivigite je 2008-04-23 per la retarkivo Wayback Machine (germane)
- ↑ P. E. A. Lenard, Ann. Pkysik, 8, p. 149, 1902; vidu la lekcion pri la Nobel-premiito Phillipp Lenard.
- ↑ [https://web.archive.org/web/20070419024649/http://www.tu-harburg.de/rzt/rzt/it/Ether.html Arkivigite je 2007-04-19 per la retarkivo Wayback Machine A. Einstein, Aether and the theory of Relativity (Etero kaj la teorio de relativeco), Universitato de Lejdeno, Nederlando, 1920]. (germane)
- ↑ H. Geiger and E. Marsden On a Diffuse Reflection of the α-Particles (Pri difuza reflekto de alfa-partikloj), Proceedings of the Royal Society, Serio A 82, p. 495–500, 1909. Arkivigite je 2008-01-02 per la retarkivo Wayback Machine (angle)
- ↑ E. Rutherford, The Scattering of α and β Particles by Matter and the Structure of the Atom (Disĵeto de α- kaj β-partikloj per materio kaj strukturo de atomo), Philosophical Magazine, Serio 6 21: p. 669–688, 1911. Arkivigite je 2008-01-14 per la retarkivo Wayback Machine (angle)
- ↑ N. Bohr, On the Constitution of Atoms and Molecules (Pri konsisto de atomoj kaj molekuloj), Philosophical Magazine, Serio 6, vol. 26. p. 1-25, 1913 Arkivigite je 2007-07-04 per la retarkivo Wayback Machine; vidu ankaŭ la lekcion pri Nobel-premiito, Erwin Schrödinger. (angle)
- ↑ P. A. M. Dirac, The Principles of Quantum Mechanics (La principoj de la kvantuma mekaniko), Oxford University Press, 1-a eldono 1930; 4-a eldono 1982. ISBN 0-19-852011-5; komparu ankaŭ kun la Ejnŝtejna teorio de elektrono citata en noto 31 supre. (angle)
- ↑ Lekcio pri la Nobel-premiitoj Richard Feynman, Julian Swinger kaj Sin-Intiro Tomonaga. (angle)
- ↑ Paul Dirac (1-a de septembro 1931). Quantised Singularities in the Electromagnetic Field (Kvantumigitaj partikularaĵoj en elektromagneta kampo) (angle) (Londono). Proceedings of the Royal Society A 133 (821) p. 60-72versio pdf. Proceedings of the Royal Society.
- ↑ Bureau International des Poids et Mesures (Buroo Internacia pri Pezoj kaj Mezuroj) (france);
- ↑ La aliaj bazaj unuoj estas kelvino (K), molo (mol), kaj kandelo (cd). Derivitaj unuoj estas, ekzemple pri areo kvadrata metro (m2), volumeno kuba metro (m3), forto neŭtono (N = kg m/s2), kaj elektra tensio volto (V = N m/A s).
- ↑ Pri historio de Sistemo Internacia (angle)
- ↑ Aliaj bazaj unuoj estas kelvino (K) kaj molo (mol). Derivitaj unuoj estas, ekzemple pri areo kvadrata centimetro (cm2), volumeno kuba centimetro (cm3), forto dino (dyn = g cm/s2), kaj elektra tensio statvolto (statV = dyn cm/Fr).
- ↑ Plena Ilustrita Vortaro 2002
- ↑ Plena Ilustrita Vortaro 2002
Fontoj[redakti | redakti fonton]
- Gillispie, Charles C., eld. 1970-1980. Dictionary of Scientific Biography (Vortaro pri scienca biografio). 16 vol. Novi Eboraci: Charles Scribner and Sons. ISBN 0-684-10114-9. + Supplement II, ed. Frederic Lawrence Holmes, 2 vols., 1990. ISBN 0-684-16962-2. angle
- Griffiths, David J. 1998. Introduction to Electrodynamics (Enkonduko al elektrodinamiko). El.. 3a. Prentice Hall. ISBN 0-13-805326-X. (france)
- Jackson, John David. 1975 Classical Electrodynamics (Klasika elektrodinamiko). Eldono 2a. Novi Eboraci: John Wiley & Sons. ISBN 0-471-43132-X. angle
- Mottelay, Paul FLeury. 1922. Bibiographical History of Electricity and Magnetism (Bibliografia historio pri elektro kaj magnetismo). Richard Clay & Sons, Ltd. ISBN 1-888262-54-0. angle
- Purcell, Edward M. 1985. Electricity and Magnetism (Elektro kaj magnetismo). Berkeley Physics Course Volume 2, Second Edition. Bostoniae: McGraw Hill. ISBN 0-07-004908-4. angle
En tiu ĉi artikolo estas uzita traduko de teksto el la artikolo Physica electromagnetica en la latina Vikipedio. (konsiderita elstara)
Eksteraj ligiloj[redakti | redakti fonton]
- Elektro kaj magnetismo de Hyperphysics angle
Vidu ankaŭ[redakti | redakti fonton]
- Atmosfera elektro
- Elektro
- Klasika elektromagnetismo
- Kvantuma elektrodinamiko
- Kvantuma kampa teorio
- Elektrostatiko
- Ekvacioj de Maxwell
- Gaŭsa leĝo
- Kulomba leĝo
- Lorenca transformo
- Magnetismo
- Magnetostatiko
- Oliver Heaviside
- Elektromagneta forto
- Elektromagneta indukto
- Elektromagneta ondo
- Magneta unupoluso
- Statika elektro

![{\displaystyle c_{0}=2,99792458\times 10^{8}\,[m/s]\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a5420f592eb60af576302213631b1dca1a4f92)





![{\displaystyle {\frac {1}{4\pi \epsilon _{o}}}=8.988\times 10^{9}\,[{\frac {Nm^{2}}{C^{2}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/682f58f643e6c1e70c81bb5e635f925dc2d6cb6f)












![{\displaystyle {\frac {\mu _{0}}{4\pi }}=10^{-7}\,[{\frac {N}{A^{2}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/001a59d8afcb21c5db872a8d06f5582d648de202)













![{\displaystyle h=6.626\times 10^{-34}\,[J.s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b1fe3c60e268e8459e486e2c2c93e1351c7f5fe)

![{\displaystyle {\frac {\mu _{0}}{4\pi }}=10^{-7}\;[{\frac {kg\;m}{A^{2}\;s^{2}}}]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/457e775eca4cfafb7cc2497b16ebcfa1810efb7e)
![{\displaystyle [C]=[A\cdot s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40e50e145deeb05fd92782f877c35790d2847ee4)
![{\displaystyle =[{\frac {N}{A\;m}}]=[{\frac {kg}{A\;s^{2}}}]\,;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bddabfd4fa6823c1c656d0959832f4553b3d7b9)


![{\displaystyle =[{\frac {dyn}{Fr}}]=[{\frac {g\;cm}{Fr\;s^{2}}}]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48a333e2bd8d4ced603d5f6c2becf1d6175e848a)

















