Sesedro
Sesedro (aŭ heksaedro) estas tridimensia geometria formo, kiun limigas ses facoj. Ĝi do estas speco de pluredro.
Regula ortangula sesedro nomiĝas kubo. Aliaj ekzemploj de sesedroj estas la paralelepipedo, la briko, la kvinlatera piramido kaj multaj aliaj.
Topologie diversaj sesedroj[redakti | redakti fonton]
Estas sep topologie diversaj konveksaj sesedroj [1], unu el kiuj estas nememspegulsimetria kaj do estadas en formoj, unu el kiuj estas spegula bildo de la aliaj. Du pluredroj estas topologie diversaj se ili havas malsamajn ordigojn de edroj, lateroj kaj verticoj, tiel ke ĝi neeblas malformigi unuon el ili en la alian simple per ŝanĝo de longoj de lateroj aŭ la anguloj inter lateroj aŭ edroj.)
Ekzemplo de ĉiu speco estas prezentita pli sube, kune kun kvantoj de lateroj ĉe la edroj kaj la kvantoj de verticoj kaj lateroj.
| Bildo | Nomo (se ekzistas) | Kvantoj de lateroj ĉe la edroj | Verticoj | Lateroj |
|---|---|---|---|---|

|
Kubo kaj topologiaj ekvivalentoj | 4,4,4,4,4,4 | 8 | 12 |

|
Kvinlatera piramido | 5,3,3,3,3,3 | 6 | 10 |

|
5,4,4,3,3,3 | 7 | 11 | |

|
5,5,4,4,3,3 | 8 | 12 | |

|
Triangula dupiramido | 3,3,3,3,3,3 | 5 | 9 |

|
4,4,4,4,3,3 | 7 | 11 | |
  (nememspegulsimetria) |
4,4,3,3,3,3 | 6 | 10 |
Estas tri pluaj topologie diversaj sesedroj, kiuj povas esti nur konkavaj:
| Bildo | Nomo (se ekzistas) | Kvantoj de lateroj ĉe la edroj | Verticoj | Lateroj |
|---|---|---|---|---|

|
4,4,3,3,3,3 | 6 | 10 | |

|
6,6,3,3,3,3 | 8 | 12 | |

|
5,5,3,3,3,3 | 7 | 11 |
Sesedroj topologie ekvivalentaj al kubo[redakti | redakti fonton]
| Kun paralelogramaj edroj: | ||||
|---|---|---|---|---|
 Kubo (6 kvadratoj) |
 Briko (3 paroj de ortanguloj) |
 Paralelepipedo (3 paroj de paralelogramoj) |
 Romboedro (3 paroj de romboj) |
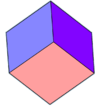 Tritranĉa kajtopluredro (6 kongruaj romboj) |
| Aliaj: | ||||
 Kvadrata trunko aŭ senpintigita kvadrata piramido (4 trapezoj kaj 2 kvadratoj) |
 Trapeza prismo (2 trapezoj kaj 4 ortanguloj) |
|||
Vidu ankaŭ[redakti | redakti fonton]
| ||||||
Eksteraj ligiloj[redakti | redakti fonton]
- ↑ Kalkulado de pluredroj. Arkivita el la originalo je 2008-07-25. Alirita 2008-01-29.
- Pluredroj kun 4-7 edroj Arkivigite je 2006-09-04 per la retarkivo Wayback Machine de Steven Dutch
