Rubando de Möbius

En matematiko, la rubando de Möbius estas certa 2-dimensia sternaĵo, tio estas, surfaco. Ĝi estas kompakta kaj ne-orientebla (sen malsamaj ena kaj ekstera flankoj) kun unu rando.
Ĝia eŭlera karakterizo estas 0.
Aliaj rilatantaj ne-orienteblaj objektoj estas la botelo de Klein kaj la reela projekcia ebeno. Rilatantaj orienteblaj objektoj estas cilindro, sfero kaj toro. Rubando de Möbius kaj cilindro estas du dimensiaj surfacoj kun rando; botelo de Klein, reela projekcia ebeno, sfero kaj toro ne havas randon.
La figuro estas nomata laŭ matematikisto kaj astronomo August Ferdinand Möbius el Leipzig kiu en 1858 malkovris la figuron. Pli malpli samtempe, sed sendepende de Möbius la matematikisto kaj fizikisto Johann Benedict Listing el Göttingen ankaŭ malkovris la bendon.
Modelo de rubando de Möbius povas facile esti kreita per preno de papera rubando kaj gluo ĝin en ringon kun tordo de unu fino je duono de la plena cirklo (180 gradoj). En eŭklida spaco estas fakte du specoj de rubandoj de Möbius ekzistas dependante de la direkto de la tordo - laŭhorloĝnadla kaj kontraŭhorloĝnadla. La rubando de Möbius estas pro tio nememspegulsimetria.
Topologia konstruado[redakti | redakti fonton]
Startu de kvadrato kaj tiam gluu kune respektivajn kolorigitajn randoj, tiel ke la sagoj kongruu. Rubando de Möbius estas priskribata kiel unuobla kvadrato ( [0,1] × [0,1] ) kun flankoj identigitaj per la rilatoj:
- (x, 0) ~ (1-x, 1) por 0 ≤ x ≤ 1
Ĉi tiu kvadrato estas fundamenta plurlatero de la rubando de Möbius.
 Sfero |
 Cilindra surfaco |
 Rubando de Möbius |
 Toro |
 Botelo de Klein |
 Reela projekcia ebeno |
Notu ke ĉi tio estas abstrakta gluado en topologia senco, por reala konstruado bezonatas longa mallarĝa rubando kaj ne kvadrato.
Geometrio kaj topologio[redakti | redakti fonton]

Eblas prezenti la rubandon de Möbius en tri-dimensia eŭklida spaco per jena parametrigo:
kie 0 ≤ u < 2π kaj -1 ≤ v ≤ 1. Ĉi tio kreas rubandon de Möbius de larĝo 1 kies centra cirklo havas radiuson 1, kuŝas en la xy ebeno kaj estas centrita je (0,0,0). La parametro u kuras ĉirkaŭ la rubando kaj v movas de unu rando al la alia.
En cilindraj polusaj koordinatoj (r,θ,z), nebarita versio de la rubando de Möbius povas esti prezentita per la ekvacio:
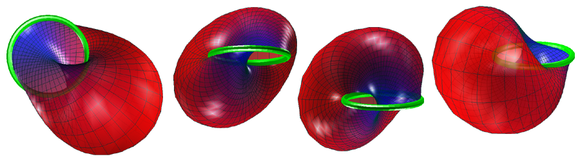
La rando de rubando de Möbius estas topologie ekvivalento al la cirklo. En la kutimaj enigoj de la rubando en Eŭklida spaco, kiel pli supre, ĉi tiu rando estas ne ordinara ebena cirklo. Tamen eblas al enigi rubando de Möbius en tri-dimensiojn tiel ke la rando estu cirklo, kaj la rezultanta figuro estas nomita kiel sudana rubando de Möbius.
Por vidi ĉi tion, unue konsideru enigon en la 3-sferon S4 konsideratan kiel subaro de R4. Parametrigo por ĉi tiu enigo estas
Ĉi tie estas uzata kompleksa skribmaniero kaj R4 estas kiel C2. La parametro kuras ekde 0 al π kaj kuras ekde 0 al 2π. Pro tio ke la enigita surfaco kuŝas tute sur S3. La rando de la rubando estas donita per (respektiva al ), kiu estas klare cirklo sur la 3-sfero.
Por ricevi enigo de la rubando de Möbius en R3 mapu S3 al R3 per rektlinia sfera projekcio. La projekcia punkto povas esti ĉiu punkto sur S3 kiu ne kuŝas sur la enigita rubando de Möbius (ĉi tio malebligas kutimajn projekciajn punktojn). Rektliniaj sferaj projekciaj mapaj cirkloj al cirkloj kaj konservas la cirklan randon de la rubando. La rezulto estas glata enigo de rubando de Möbius en R3 kun cirkla rando kaj ne sinsekcanta.
Vidu ankaŭ[redakti | redakti fonton]
- Botelo de Klein
- Reela projekcia ebeno
- Cilindro
- Sfero
- Toro
- Topologio
- Algebra topologio
- Listo de cikloj
- Ciklo
- Stranga ciklo
- Kruco-ĉapo
- Mœbius
Eksteraj ligiloj[redakti | redakti fonton]
- Angla paĝo pri la bendo de Möbius
- Tridimensia kaj turna rubando de Möbius
- Proteino kun topologia tordo
- Virtuala marŝo en la suna vento
- Johann Benedict Listing Arkivigite je 2008-03-31 per la retarkivo Wayback Machine
- Eric W. Weisstein, Rubando de Möbius en MathWorld.
- Rubando de Möbius je tranĉi-la-nodon
- Trikita versio
- h2g2 - La miriga rubando de Möbius
- Batalo de Möbius en xkcd.
- Tordo sur la rubando de Möbius: esploristoj ellaboras la formon de papera rubando[rompita ligilo]
- . Nature - Naturo (ĵurnalo). Alirita 2006-07-16.
- Sudana rubando de Möbius Arkivigite je 2008-07-06 per la retarkivo Wayback Machine











