Reela projekcia ebeno
En matematiko, la reela projekcia ebeno estas speco de projekcia ebeno, spaco de linioj en R3 pasantaj tra la fonto. Ĝi estas 2-dimensia sternaĵo, tio estas, surfaco. Ĝi estas kompakta kaj ne-orientebla (sen malsamaj ena kaj ekstera flankoj). Reela projekcia ebeno ne povas esti enigita en kutiman tri-dimensian eŭklidan spacon sen sekco de si.
Ĝia eŭlera karakterizo estas 1 kaj do ĝia genro estas 1.
Startu de kvadrato kaj tiam gluu kune respektivajn kolorigitajn randoj, tiel ke la sagoj kongruu. Reela projekcia ebeno povas esti prezentita kiel kvocienta spaco, unuobla kvadrato ( [0,1] × [0,1] ) kun flankoj identigitaj jene:
- (0, y) ~ (1, 1-y) por 0 ≤ y ≤ 1
- (x, 0) ~ (1-x, 1) por 0 ≤ x ≤ 1
Noto ke ĉi tio estas abstrakta gluado en topologia senco.
Ĉi tiu kvadrato estas fundamenta plurlatero de la botelo de Klein.
 Sfero |
 Cilindra surfaco |
 Rubando de Möbius |
 Toro |
 Botelo de Klein |
 Reela projekcia ebeno |
La filmo de Möbius kun sola rando, povas fermiĝi en projekcian ebenon per gluado de kontraŭa malfermitaj randoj kune. En komparo la botelo de Klein estas filmo de Möbius fermita en cilindron.
Konstruado[redakti | redakti fonton]
Estu sfero, kaj estu la ĉefcirkloj de la sfero esti linioj, kaj estu paroj de antipodaj punktoj la punktoj. Ekvivalente, oni identigu ĉiun punkton sur la sfero kun ĝia antipoda punkto.
La rezultanta spaco obeas la aksiomojn de projekcia ebeno:
- Ĉiu paro de malsamaj ĉefcirkloj intersekciĝas je du antipodaj punktoj.
- Ĉiuj du malsamaj paroj de antipodaj punktoj kuŝas sur sola ĉefcirklo.
Ĉi tio estas la reela projekcia ebeno.
La kvocienta mapo de la sfero sur la reela projekcia ebeno estas fakte (du-al-unu) kovranta mapo. La fundamenta grupo de reela projekcia ebeno estas la cikla grupo de ordo 2, kio estas grupo de entjeroj module 2. Eblas ekzemple preni la ciklon AB de la figuro pli supre kiel la generilo.
Konstruado de reela projekcia ebeno povas esti farita surbaze de filmo de Möbius. Se glui la (solan) randon de la filmo de Möbius al si en la korekta direkto rezultiĝas la projekcia ebeno. Ekvivalente, se glui diskon laŭ la rando de filmo de Möbius rezultiĝas la projekcia ebeno.
La pruvo ke la projekcia ebeno ne povas esti enigita en tri-dimensian eŭklidan spacon estas jena. Se ĝi estus enigita, ĝi barus kompaktan regionon en tri-dimensia spaco laŭ la ĝeneraligita jordana kurba teoremo. La eksteren-montranta unuobla normala vektora kampo devus tiam doni orientiĝon de la randa sternaĵo, sed la randa sternaĵo devus esti projekcia spaco, kiu estas ne orientebla.
La projekcia ebeno ne povas esti enigita (tio estas sen sinsekco) en tri-dimensian spacon. Tamen, ĝi povas esti mergita (lokaj najbaraĵoj ne havas sinsekcojn). Surfaco de Boy estas ekzemplo de mergo.
| Surfaco de Boy | |||
 De antaŭo |
 De malantaŭo |

|

|

|

|

| |
| Vidu ĉi tie animacion de la surfaco de Boy | |||
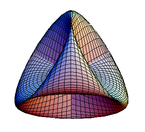
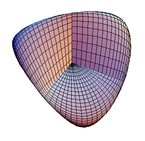
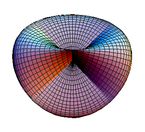
La roma surfaco estas pli degenera mapo de la projekcia ebeno en 3-spacon, enhavanta kruco-ĉapon.
| Roma surfaco | |||

|
|
|
|

Simpla pluredra prezento de la reela projekcia ebeno estas la kvar-duon-sesedro.
La duon-kubo, duon-dekduedro,kaj duon-dudekedro, kiuj estas abstraktaj regulaj hiperpluredroj, povas esti konstruitaj kiel regulaj kahelaroj en la projekcia ebeno.
Enigo en 4-dimensian spacon[redakti | redakti fonton]
La projekcia ebeno povas esti enigita en 4-dimensian eŭklidan spacon. Uzante homogenajn koordinatojn, la projekcia ebeno respektivas al punktoj
tia ke
- x2+y2+z2=1
kun noto pri la rilato
Enigo enen de R4 estas donita per la funkcio
Ĉi tiu enigo donas projekcion enen de R3 kiu estas la roma surfaco.
Homogenaj koordinatoj[redakti | redakti fonton]
La aro de linioj en la ebeno povas esti prezentita per homogenaj koordinatoj. Linio ax+by+c=0 povas esti prezentita kiel (a:b:c). Ĉi tiuj koordinatoj havas la ekvivalentrilaton (a:b:c)=(da:db:dc) por ĉiu ne nula valoro d. De ĉi tie malsamaj prezentoj de la sama linio dax+dby+dc=0 havas la samajn koordinatojn. La aro de koordinatoj (a:b:1) donas la kutiman reelan ebenon, kaj la aro de koordinatoj (a:b:0) difinas linion je malfinio.
Pli alta genro[redakti | redakti fonton]
La artikolo fundamenta plurlatero provizas priskribon de la reelaj projekciaj ebenoj de pli altaj genroj.
Vidu ankaŭ[redakti | redakti fonton]
- Projekcia spaco
- Neegalaĵo de Pu por reela projekcia ebeno
- Filmo de Möbius
- Botelo de Klein
- Cilindro
- Sfero
- Toro



