Surfaco
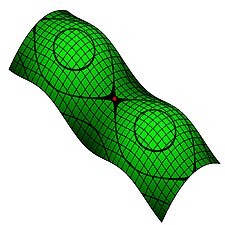
En matematiko, precipe en geometrio kaj topologio, surfaco estas du-dimensia sternaĵo. La plej kutimaj ekzemploj estas tiuj, kiuj estas randoj de solidaj objektoj en ordinara tri-dimensia eŭklida spaco E3. Estas ankaŭ pli ekzotikaj surfacoj, kiuj estas tiel torditaj, ke ili ne povas esti enigitaj en tri-dimensian spacon (termino enigo subkomprenas, ke ne aperas sin-intersekcoj).
Surfaco povas esti difinita kaj konstruita kaj per la abstrakta apriora topologia difino donita pli sube, kaj kiel subaro de eŭklidaj spaco, kutime 3-dimensia E3. En historio de matematiko konsidero de surfacoj en E3 aperis pli frue.
Tio, ke surfaco estas du-dimensia, signifas, ke ĉirkaŭ ĉiu punkto estas koordinata fliko, sur kiu du-dimensia koordinatsistemo estas difinita. Ekzemple la surfaco de la Tero estas (ideale) du-dimensia sfero, kaj latitudo kaj longitudo provizas koordinatojn sur ĝi ĉie ekster je la internacia datlinio kaj je la polusoj, kie longitudo estas nedifinita. Ĉi tiu ekzemplo ilustras, ke ĝenerale ne eblas etendi iun ajn koordinatan flikon al la tuta surfaco. Surfacoj, same kiel sternaĵoj de ĉiuj dimensioj, estas kutime konstruitaj per kunig-flikado da multaj koordinatsistemoj.
Surfacoj estas aplikataj en fiziko, inĝenierado, komputila grafiko kaj multaj aliaj fakoj, precipe tiam, kiam ili prezentas la surfacojn de fizikaj objektoj. Ekzemple koncerne al analizado de aerodinamikaj propraĵoj de iu objekto necesas, konsideri fluon de aero laŭ ties surfaco, dum eno de la objekto plejofte ne gravas.
Geometrio[redakti | redakti fonton]
Sfero kaj rando de pluredro estas ekzemploj de surfacoj en geometrio. Glata surfaco estas surfaco, ĉe kiu ĉiu punkto de ĝi havas najbaraĵon difeomorfan al iu malfermita aro en E2. Ĉi tio permesas aplikon de infinitezima kalkulo al la surfaco.
Kompleksa surfaco estas kompleksa 2-dimensia sternaĵo kaj tiel reela 4-sternaĵo; do ĝi ne estas surfaco en la antaŭe priskribita senco.
Difinoj[redakti | redakti fonton]
 Sfero povas esti difinita - per parametroj jene x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ aŭ implice jene x2 + y2 + z2 - r2 = 0. Eksplicita difino z = (r2 - x2 - y2)1/2 donas nur duonon de sfero. |
Implice difinita surfaco estas situo de nuloj de funkcio F, alivorte tiaj (x, y, z), ke F(x, y, z)=0. La funkcio F(x, y, z) estas de R3 al R. Se la funkcio F estas polinoma funkcio de 3 variabloj, la surfaco estas algebra surfaco. Grado de la polinomo estas tiam grado de la surfaco. Algebra surfaco de grado 2 estas kvadriko.
Povas okazi, ke implica surfaco ne havas geometrian formon, ĉar neniu punkto kontentigas la ekvacion. Ĉi tia surfaco estas nomata kiel imaginara surfaco. Ekzemple ekvacio
- x2 + y2 + z2 + r2 = 0
priskribas imaginaran sferon. Vidu en artikolo kvadriko por pluaj ekzemploj.
Parametre difinita surfaco estas bildo de kontinua injekta enĵeta funkcio de R2 al R3. Ekvivalente povas esti donitaj tri funkcioj R2 al R, kiuj priskribas la koordinatojn aparte:
- x = X(u, v)
- y = Y(u, v)
- z = Z(u, v)
Turna surfaco povas esti konsiderata kiel speciala speco de parametra surfaco.
Eksplicite difinita surfaco estas tiu, ĉe kiu eblas, skribi unu eron el la variabloj x, y, z kiel funkcion de du la ceteraj
- z=f(x, y)
aŭ
- x=f(y, z)
aŭ
- y=f(x, z)
Ĉi tiuj variantoj estas ĝenerale ekvivalentaj ,ĉar eblas fari ŝanĝon de koordinatoj por trairi de unu varianto al la alia, tiel plu estas diskutata nur varianto z=f(x, y). Tamen sen ŝanĝo de koordinatoj trairi de unu varianto al la alia ne ĉiam eblas. Ekzemple ebeno 2x+3y+z+1=0 povas esti ekvivalente skribita kiel x=-(3y+z+1)/2 aŭ y=-(2x+z+1)/3 aŭ z=-2x-3y-1. Sed ebeno z=2 kaj duonsfero z=(r2 - x2 - y2)1/2 ne povas esti reskribitaj en formo x=f(y, z) aŭ y=f(x, z). Ebeno z=2x-1 povas esti ekvivalente skribita kiel x=(z+1)/2 , sed ne povas esti skribita en formo y=f(x, z).
Eblas ankaŭ difini parametrajn, eksplicitajn kaj implicajn surfacojn en pli alte dimensiaj eŭklidaj spacoj En.
Glateco[redakti | redakti fonton]
Glata surfaco estas surfaco, kiu havas tanĝantan ebenon en ĉiu punkto. La kondiĉoj de glateco estas donitaj pli sube.
- Implice difinita surfaco F(x, y, z)=0 estas glata surfaco, se funkcio F(x, y, z) estas glata funkcio, kies gradiento estas nenie nulo (F havas kontinuajn partajn derivaĵojn je x, y, z, kaj en ĉiu punkto almenaŭ unu da ili estas ne nulo). Se la kondiĉo de ne nuliĝo de gradiento ne ĉie veras, tiam povas okazi specialaĵoj.
- :
- Parametre difinita surfaco
- : x = X(u, v)
- : y = Y(u, v)
- : z = Z(u, v)
- : estas glata surfaco, se la funkciaj difinas reciproke unuvaloran surĵeton inter (x, y, z) sur la surfaco kaj (u, v) kaj funkcioj X, Y, Z estas kontinue diferencialeblaj kaj estas kontentigita kondiĉo de nedegenereco
- :
- Eksplicite difinita surfaco z=f(x, y) estas glata surfaco, se la funkcio f' estas kontinue diferencialebla.
Plua postulo estas, ke la surfaco havu kurbecon, por ĝi bazonatas ekzisto de la duaj derivaĵoj de funkcioj, kiuj difinas la surfacon.
En diferenciala kaj algebra geometrio estas studataj specialaĵoj - sin-intersekcoj, kuspoj, kaj tiel plu de surfacoj.
Tanĝanta ebeno kaj normalo[redakti | redakti fonton]
Normalo estas vektoro perpendikulara al ebeno tanĝanta al la surfaco en donita punkto.
| Normalo | Tanĝanta ebeno | |
|---|---|---|
| Implice difinita surfaco | ||
| Eksplicite difinita surfaco | ||
| Parametre difinita surfaco | ||
| kie | ||
Areo[redakti | redakti fonton]
| Eksplicite difinita surfaco | |
|---|---|
| Parametre difinita surfaco | aŭ |
| kie |
Rimana metriko[redakti | redakti fonton]
Glataj surfacoj kun rimana metriko estas de fundamenta graveco en diferenciala geometrio. Rimana metriko donas al surfaco nociojn de geodezia kurbo, distanco, angulo, areo. Ĝi ankaŭ donas la gaŭsan kurbecon, kiu priskribas kiel liniita aŭ kurba la surfaco estas je ĉiu punkto. Gaŭsa kurbeco estas rigida, geometria propraĵo kaj estas ne konservata per ĝeneralaj difeomorfiojg de la surfaco. Tamen teoremo de Gauss-Bonnet por fermitaj surfacoj statas, ke integralo de la gaŭsa kurbeco K tra la tuta surfaco S estas difinita per la eŭlera karakterizo:
Ĉi tiu rezulto montras profundan interrilaton inter geometrio kaj topologio de surfacoj (kaj, en malpli granda amplekso, de pli alte dimensiaj sternaĵoj).
Alia maniero de konsidero de surfacoj en geometrio estas la uzo de la kompleksa domajno. Kompleksa unu-sternaĵo estas glata orientita surfaco - ankaŭ nomata kiel rimana surfaco. Ĉiu kompleksa nesingulara algebra kurbo vidata kiel sternaĵo de duoble pli multaj reelaj koordinatoj estas rimana surfaco.
Unu versio de la samformiga teoremo de Henri Poincaré) statas, ke ĉiu rimana metriko sur orientita fermita surfaco estas konforme ekvivalenta al esence unika metriko de konstanta kurbeco. Ĉi tio provizas deirpunkton por unu el manieroj de teorio de Teichmüller, kiu provizas pli fajnan klasifikon de rimanaj surfacoj ol en topologio nur per eŭlera karakterizo.
Topologio[redakti | redakti fonton]
Topologia surfaco kun rando aŭ simple surfaco kun rando estas topologia spaco de Hausdorff en kiu ĉiu ne-randa punkto havas malfermitan najbaraĵon homeomorfan al iu malfermita subaro de la fermita duono de eŭklida 2-spaco E2. La najbaraĵo, kune kun la homeomorfio al eŭklida spaco, estas nomata kiel koordinata abako.
La aro de punktoj kiuj havas malfermita najbaraĵon homeomorfan al E2 estas nomata kiel la eno de la surfaco; ĝi estas ĉiam ne-malplena. La komplemento de la eno estas nomata kiel la rando; ĝi estas unu-dimensia sternaĵo, aŭ unio de fermitaj kurboj. La plej simpla ekzemplo de surfaco kun rando estas la fermita disko en E2; ĝia rando estas cirklo. Aliaj konataj ekzemploj estas finia cilindra surfaco kaj rubando de Möbius. Rando de finia cilindra surfaco estas unio de du kongruaj kurboj, rando de disko kaj de rubando de Möbius konsistas el nur unu kurbo.
Surfaco kun malplena rando estas senranda surfaco. (Iam la vorto surfaco, uzata sola, temas nur pri senrandaj surfacoj.) Fermita surfaco estas tiu kiu estas senranda kaj kompakta spaco. La 2-dimensia sfero, 2-dimensia toro, kaj reela projekcia ebeno estas fermita surfacoj.
Rubando de Möbius estas surfaco kun nur unu flanko. Ĝenerale, surfaco estas orientebla se ĝi ne enhavas homeomorfajn kopiojn de rubando de Möbius; intuicie, se ĝi havas du malsamajn flankojn. Ekzemple, 2-sfero kaj toro estas orienteblaj, kaj la reela projekcia ebeno estas ne orientebla (ĉar post forviŝo de iu disko la reela projekcia ebeno transformiĝas en la rubandon de Möbius).
Enigo[redakti | redakti fonton]
La eniga teoremo de Whitney ĉe surfacoj statas ke ĉiu surfaco difinita abstrakte topologie kiel sternaĵo povas esti enigita homeomorfie en E4.
Pli forte, ĉiu kompakta surfaco kiu estas orientebla aŭ havas randon povas esti enigita en E3. Povas okazi ke surfaco kiu ne kontentigas la kondiĉoj ne povas esti enigita en E3, ekzemple la reela projekcia ebeno, kiu estas kompakta, ne-orientebla kaj sen rando, ne povas esti enigita en E3. Surfacoj de Steiner, inkluzivante surfacon de Boy, roman surfaco kaj kruci-ĉapon, estas mergoj de la reela projekcia ebeno enen E3. Ĉi tiuj surfacoj estas singularaj tie kie la mergoj sekcas sin.
La kornita sfero de Aleksander estas malnormala enigo de la du-sfero en la tri-sferon.
La elektita enigo de surfaco en alian spacon estas ekstera informo, ĝi ne estas esenca al la surfaco mem. Ekzemple, toro povas esti enigita en E3 en la kutima maniero aŭ en nodita maniero. La du enigitaj toroj estas homeomorfaj sed ne izotopaj; ili estas topologie ekvivalentaj, sed iliaj enigoj ne estas topologie ekvivalentaj.
 Kutima enigo de toro |
 Nodita toro |
Koneksa sumo[redakti | redakti fonton]
Koneksa sumo de du surfacoj M kaj N, skribata kiel M # N, estas ricevata per forpreno de disko de ĉiu el ili kaj gluado ilin kune laŭ la randoj aperintaj dum la forpreno. La eŭlera karakterizo de M # N estas sumo de la eŭleraj karakterizoj de la fontaj surfacoj minus 2:
- χ(M # N) = χ(M) + χ(N) - 2
La sfero S estas neŭtra elemento por koneksa sumo, ĉar S # M = M. Ĉi tio estas ĉar forviŝo de disko de la sfero lasas diskon, kiu simple anstataŭigas la diskon forviŝitan de M antaŭ la gluado.
Koneksa sumo kun la toro T estas alfikso de anso al la alia fonta surfaco M de la sumo. Se M estas orientebla, tiam T # M estas ne homeomorfa al M. La koneksa sumado povas esti ripetita por alfiksi iun kvanton g de ansoj al M.
Koneksa sumo de du reelaj projekciaj ebenoj estas botelo de Klein. Koneksa sumo de reela projekcia ebeno kaj botelo de Klein estas homeomorfa al la koneksa sumo de reela projekcia ebeno kun la toro. Ĉiu koneksa sumo engaĝanta reelan projekcian ebenon estas neorientebla.
Klasifiko de fermitaj surfacoj[redakti | redakti fonton]
Ĉiu fermita surfaco estas homeomorfa al iu membro de unu el ĉi tiuj tri familioj:
- Sfero
- Koneksa sumo de g toroj, g ≥ 1
- Koneksa sumo de k reelaj projekciaj ebenoj, k ≥ 1
La surfacoj en la unuaj du familioj estas orienteblaj. Estas oportune komponi la du familiojn per preno ke la sfero estas koneksa sumo de 0 toroj. La kvanto g de toroj estas nomata kiel la genro de la surfaco. La sfero kaj la toro havas eŭlerajn karakterizojn 2 kaj 0 respektive, kaj tiel plu eŭlera karakterizo de la koneksa sumo de g toroj estas 2-2g.
La surfacoj en la tria familio estas neorienteblaj. Pro tio ke eŭlera karakterizo de la reela projekcia ebeno estas 1, eŭlera karakterizo de la koneksa sumo de k de ili estas 2-k.
El ĉi tio sekvas ke fermita surfaco estas difinita, supren ĝis homeomorfio, per du pecoj de informo: ĝia eŭlera karakterizo, kaj ĉu ĝi estas orientebla ĉu ne. En aliaj vortoj, eŭlera karakterizo kaj orientebleco plene klasifikas fermitajn surfacoj supren ĝis homeomorfio.
Du glataj surfacoj estas difeomorfaj se kaj nur se ili estas homeomorfaj. (La analoga rezulto ne veras por pli alte dimensiaj sternaĵoj.) Tial fermita surfaco estas klasifikita supren ĝis difeomorfio per ĝia eŭlera karakterizo kaj orientebleco.
Konstruado surbaze de fundamenta plurlatero[redakti | redakti fonton]
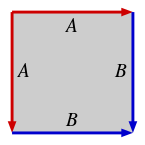
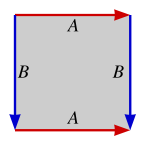
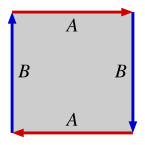
Ĉiu fermita surfaco povas esti konstruita surbaze de orientita plurlatero kun para kvanto de lateroj, nomata kiel fundamenta plurlatero de la surfaco, per laŭduopa identigo de lateroj de la plurlatero. Ekzemple, ĉe ĉiu plurlatero (kvadrato en la okazo) pli sube, kunigo de lateroj laŭ kongruantaj markoj (A kun A, B kun B), tiel ke la kunigataj sagoj montru en la sama direkto, donas la surfacojn.

|

|

|

|
|
|

|
|
| Sfero | Toro | Botelo de Klein | Reela projekcia ebeno |
Ĉiu fundamenta plurlatero povas esti skribita signmaniere kiel sekvas. Komencu je iu vertico, kaj procedu ĉirkaŭ la perimetro de la plurlatero en iu direkto al denova renkonto de la startanta vertico. Dum ĉi tiu trairo, skribu la markon sur ĉiu latero en ordo, kun supra indekso -1 se la lateraj sago kontraŭas al direkto de la trairo. Por la kvar variantoj pli supre, se trairi laŭhorloĝnadle startante je la supra maldekstra vertico, liveriĝas
- Sfero:
- Toro:
- Botelo de Klein:
- Reela projekcia ebeno:
La esprimo tial derivita de fundamenta plurlatero de surfaco rilatas al prezento de la fundamenta grupo de la surfaco kun la plurlateraj lateroj markoj kiel generiloj. Ĉi tio estas konsekvenco de teoremo de Seifert-van Kampen.
Ankaŭ surfaco kun rando povas esti konstruita surbaze de plurlatero, sed en ĉi tiu okazo ne ĉiuj lateroj de la plurlatero estas konektitaj. La nekonektitaj lateroj formas randon de la surfaco.

|
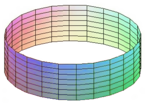
|
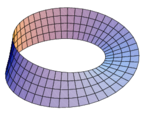
|
 (neniu identigo) |

|

|
| Disko | Cilindra surfaco | Rubando de Möbius |
Kvocientaj spacoj[redakti | redakti fonton]
Gluado de randoj de plurlateroj estas speco de procezo de kreo de kvocienta spaco. La kvocienta koncepto povas esti aplikita pli ĝenerale por produkti novajn aŭ alternativajn konstruojn de surfacoj. Ekzemple, reela projekcia ebeno povas esti ricevita kiel la kvociento de la sfero per identigo de ĉiuj paroj de kontraŭaj punktoj sur la sfero. Alia ekzemplo de kvociento estas la koneksa sumo.
Vidu ankaŭ[redakti | redakti fonton]
- Algebra surfaco
- Diferenciala geometrio de surfacoj
- Rimana metriko
- Propraĵoj
- Iuj surfacoj
- Kurbo (1-sternaĵo)
- 3-sternaĵo
- 4-sternaĵo
- 5-sternaĵo
- Spaco
- Hipersurfaco
Eksteraj ligiloj[redakti | redakti fonton]
- André Gramain. (1984) Topology of Surfaces - Topologio de surfacoj. BCS Associates. ISBN 0-914351-01-X. [1] Arkivigite je 2017-07-09 per la retarkivo Wayback Machine (Originala kurso de 1969 ... 1970)
- Math Surfaca Galerio, kun 60 ~surfacoj kaj Java Apleto por aktuala turnado vidanta
- Math Surfaca Animacio, kun JavaScript (Kanvaso HTML) por deka surfaca turnado vidanta[rompita ligilo]












![{\displaystyle \iint \,|[{\dot {r}}_{u}\times {\dot {r}}_{v}]|\;\mathrm {d} \,u\,\mathrm {d} \,v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df5afba40cb60c0f345573e8aa2a3d63c5f2278a)





