Senpintigita dudekedro
| Senpintigita dudekedro | |

| |
| |
| Klaku por rigardi turnantan bildon | |
| Vertica figuro | 5.6.6 |
| Bildo de vertico | 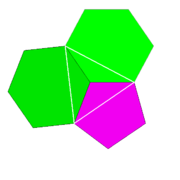
|
| Bildo de reto | 
|
| Simbolo de Wythoff | 2 5 | 3 |
| Simbolo de Schläfli | t{3,5} |
| Figuro de Coxeter-Dynkin | |
| Indeksoj | U25 C27 W9 |
| Simbolo de Bowers | Ti |
| Verticoj | 60 |
| Lateroj | 90 |
| Edroj | 32 |
| Edroj detale | 12{5}+20{6} |
| χ | 2 |
| Geometria simetria grupo | Ih |
| Duala | Kvinlateropiramidigita dekduedro |
| Bildo de duala | 
|
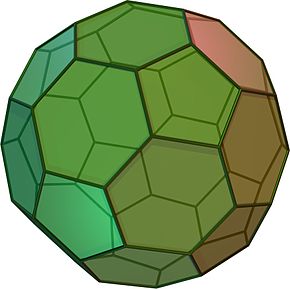
La senpintigita dudekedro estas pluredro, arkimeda solido. Ĝi havas 12 regulajn kvinlaterajn edrojn, 20 regulajn seslaterajn edrojn, 60 verticojn kaj 90 laterojn.
Karteziaj koordinatoj[redakti | redakti fonton]
Karteziaj koordinatoj de verticoj de senpintigita dudekedro centrita je (0,0,0) de latera longo 2 estas:
- (0,±1,±3φ)
- (±1,±3φ,0)
- (±3φ,0,±1)
- (±2,±(1+2φ),±φ)
- (±(1+2φ),±φ,±2)
- (±φ,±2,±(1+2φ))
- (±1,±(2+φ),±2φ)
- (±(2+φ),±2φ,±1)
- (±2φ,±1,±(2+φ))
- kie φ = (1+√5)/2 estas la ora proporcio.
Ĉiuj verticoj estas sur sfero centrita je (0,0,0) de radiuso (9φ+10)1/2.
Areo kaj volumeno[redakti | redakti fonton]
La areo A kaj la volumeno V de la senpintigita dudekedro de randa longo a estas:
Geometriaj rilatoj[redakti | redakti fonton]
Ĉi tiu pluredro povas esti konstruita de dudekedro per senpintigo (forhako) de la 12 verticoj tiel ke unu triono de ĉiu latero estas dehakita je ĉiu el ambaŭ ĝiaj finoj. Ĉi tio kreas 12 novajn kvinlaterajn edrojn, kaj aliformigas la originalajn 20 triangulajn edrojn en regulajn seslaterojn.
La senpintigita dudekedro ekzistas en la aro de senpintigitaj formoj inter dekduedro kaj dudekedro:

|

|

|

|

|
| Dekduedro | Senpintigita dekduedro | Dudek-dekduedro | Senpintigita dudekedro | Dudekedro |
Aplikoj[redakti | redakti fonton]

Futbala pilko estas ekzemplo de senpintigita dudekedro. La pilko havas la sama manieron de interkonekso de regulaj kvinlateroj kaj regulaj seslateroj, sed estas pli sfera pro ena aera premo kaj elasteco de la materialo.
Ĉi tiu formo estis ankaŭ la konfiguro de la lensoj uzita por fokusado la eksplodaj ondoj en iuk atomaj bomboj [1].
La senpintigita dudekedro estas la formo de la karbona fulerena molekulo C60.Ĝia diametro estas proksimume 10−9 metroj.
Senpintigitaj dudekedroj en la artoj[redakti | redakti fonton]
Senpintigita dudekedro kun "solidaj randoj" estas desegnaĵo per Luca Pacioli en La Klerika Proporcio.
Vidu ankaŭ[redakti | redakti fonton]
Referencoj[redakti | redakti fonton]
- ↑ (Richard Rhodes. Dark Sun: The Making of the Hydrogen Bomb. - Malhela Suno: La faro de la hidrogena bombo, ISBN 0-684-82414-0. Touchstone Books, 1996., p. 195)
- Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)
Eksteraj ligiloj[redakti | redakti fonton]
- Eric W. Weisstein, Senpintigita dudekedro en MathWorld.
- La unuformaj pluredroj
- Virtualaj realaj pluredroj - la enciklopedio de pluredroj
- Paperaj modeloj de pluredroj
- Senpintigita dudekedro montrata per JVM


